Sic Bo - Learn to Calculate Your Chances to Win in Video
Hi guys, this is Mike.
In this segment, you will understand how to determine the chances of specific outcomes within the game. Sic Bo To put it simply, Sic Bo is a traditional Chinese game that involves rolling three dice, with numerous betting options to explore.

What I\"m going to do :
Since many forum members have voiced concerns about the length of my videos, in this initial video , I will break down how to compute the probabilities of rolling total values ranging from 3 to 18 with three dice, in addition to the likelihood of rolling 0, 1, 2, or 3 of a specific die face.
With these fundamental questions addressed…
…we can transition to the next video and evaluate the potential value associated with the various betting options in Sic Bo.
Let’s tackle the question: "What is the likelihood of obtaining any specific total with three dice that each have six sides?\" This approach can be applied regardless of how many dice are used.
I would like to acknowledge Robert Goodhand from Somerset, UK, for sharing this insightful technique, which is further elaborated in my work. Ask the Wizard column 264. I\"m going to share it with you now.
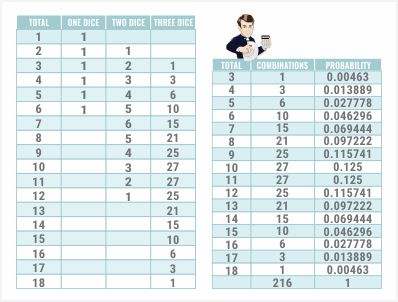
First and foremost, we should outline five placeholder squares. You’ll soon see their significance. Now, I will provide a list of every possible total ranging from 1 to 18. When rolling a single die, it's clear that there’s only one way to achieve a 1, 2, or 6.
Each die face obviously has just one outcome. With a pair of dice, you’ll need to sum the values of the left column, referred to here as column B, beginning with the first cell and moving upward to include the five cells above it.
In the case right now…
Currently, I'm referencing cell C8, which represents how many ways you can roll a sum of two with two dice. I'm constructing this by adding the values from cells B2 to B7. If any cell is left empty, Excel will correctly interpret it as zero.
I simply copy that formula down through all the totals up to 12. For a total of two, there is one possible way to achieve it. For a total of three, there are two possible outcomes. For a total of four, there are three different combinations.
Well, why does this work?
Let’s take a moment to examine the total of two. Achieving this total requires that the first die shows a one, and similarly, the second die must also show a one. Thus, there’s only one way for the first die to show a one, as well as one way for the second die.
For a total of three, there are two different combinations. One involves the first die being a one, with the second die showing a two , and the other occurs when the first die is a two and the second is a one. To achieve a total of four, the first die must demonstrate a value from one to three.
For a total of five..
The first die has to be within the total range from one to four. As long as the first die meets this requirement, there exists one way the next die can fulfill the required total.
Let\"s go on to three dice
The same approach applies here. We can replicate this method seamlessly. I can select any point within the range we previously established for the calculations. I’ll copy the same formula one cell over to the right and then drag it down to find the combinations for all totals from 3 to 18 using three dice.
For example:
There is one method to achieve a total of three, three methods for hitting a total of four, six methods for rolling a total of five, and so on. But why does this work? You might be wondering. Let’s analyze the total of seven as an illustrative example. To reach a total of seven with three dice, you might combine a total of two from two dice and then add a five.
From the two dice summing to two, there’s a singular method. Another way to achieve this is if the initial two dice come to three and you then add a four from the third die. As we discovered, there are two ways the initial two dice can total to three and three possible combinations for achieving four.
To get a total of seven …
…the first two dice need to total between two to six. We previously noted that the cumulative count of methods to achieve this is summed from one to five, which gives us a total of 15. Let’s create a convenient table to summarize this information. Once more, here is your total.
Here are the combinations :
Now, let’s add that up to get 216. Does that number ring a bell? Perhaps it resembles the outcome of six raised to the third power.
Finally, let’s determine the likelihood of each total:
We simply divide the number of combinations by the total outcomes. This will yield the probability of rolling any specified total from 3 to 18. Next, we ought to look into the probability of rolling any specific die face from zero to three times. Sic Bo features six distinct bets, one for each die face.
If the player’s chosen face appears once, they earn at a rate of one to one. If it appears twice, the odds are two to one, and if it appears three times, it’s three to one. A common mistake is to incorrectly sum probabilities when dealing with multiple events, as each die operates as an independent entity.
We do not add, we multiply.
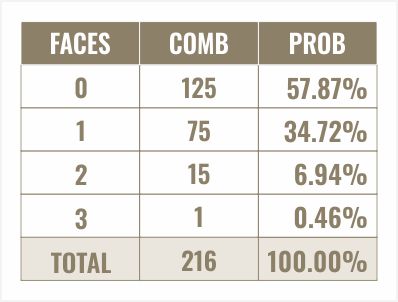
I prefer to approach things from a combinations perspective first. Take, for instance, if you select the six. What's the number of different combinations where the six appears on all three dice? The answer is straightforward—there's only one way for this to occur: 6-6-6. But what about two appearances?
For example:
This could manifest in several ways, such as 6-6-4, 2-6-6, or 6-1-6, resulting in two of the dice showing six while one shows a different number. The 'different number' can be any of the five other faces. Therefore, the total methods for rolling your selected number face twice among three dice sums up to 15.
What about the instances when your die face appears just once?
For this situation, the remaining two dice, which do not display your chosen number, could show any one of five other outcomes. We multiply 5 by 5 since each of them must be different from six or the number you chose, leading to 5 x 5 for the other two dice.
Finally…
...and then we multiply by three, as your selected die face could appear on any of the three dice. Consequently, the total combinations for your chosen face appearing just once is 5 x 5 x 3, equating to 75. For example, if the face chosen is six, it could appear in various combinations like 6-1-2, 1-4-6, or 2-6-3.
What about the combinations for not rolling the selected die face at all?
In this case, each of the three dice can showcase one of five alternative outcomes. Thus, the combinations are 5 x 5 x 5 for three dice not displaying your desired face, amounting to 125 combinations. Adding up all these combinations leads us back to 216. This number seems quite familiar, resembling six raised to the power of three, which indicates I must have been on the right track.
Finally, let’s verify the probabilities:
We can determine the probability by dividing the number of combinations by the total. Let’s express that in percentages. Here, we observe the probabilities: rolling your selected face zero times is 57.87%, one time is 34.72%, twice is 6.94%, and three times is a mere 0.46%.
I trust this explanation was comprehensive. I look forward to seeing you for part two, where I will explore the odds associated with various Sic Bo bets.
Thanks for watching.
This document has been prepared using advanced HTML editing tools. Click here and test it for free.


