Video on the Odds of Achieving a Flawless Bracket
Hello, I'm Mike, and in this video, I'll be exploring the question: What are the odds of creating a perfect March Madness bracket?
I’m going to assume you already have some background knowledge. basic knowledge about how it works To summarize briefly, there are 64 basketball teams engaged in a knockout tournament format, which results in a total of 63 games played.
These teams are categorized into four separate divisions , where the first round pits the top-seeded team against the lowest-seeded team (the 16th seed), the second seed faces the 15th, the third seed goes up against the 14th, and so forth. The winners of the first round advance to face off in the second round, ultimately leading to a single champion.
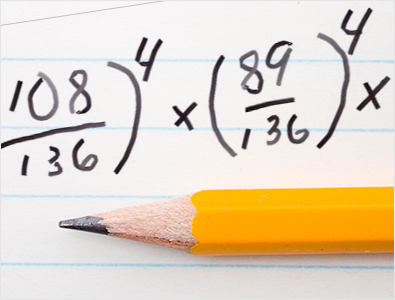
Now every March..
The media often discusses the odds of successfully completing a perfect bracket, and the statistic of 1 in 9 quintillion, 223 quadrillion, 372 trillion, 36 billion, 854 million, 781 thousand sends chills down my spine. This figure represents the likelihood of accurately forecasting 63 consecutive coin flips. It's safe to say that no one fills out a March Madness bracket in such a way, considering that some teams are clearly superior to others; for instance, a 1 seed is indisputably more talented than a 16 seed.
Before I go any further..
I need to mention that this video was filmed in April 2018, which means it's based on every March Madness game played from 1985 up until 2018. Additionally, I want to touch upon another video where the presenter claims that using a certain strategy, which he doesn't explain, the odds of a perfect bracket stand at 1 in 128 billion. This figure aligns fairly closely with my own calculations. YouTube by a professor, Jeff Bergen I would invite Professor Bergen to clarify how he derives that statistic, but I'll take the time to explain how I arrived at my own. My method is quite straightforward: you consistently choose the higher-seeded team in every game, ultimately leaving you with four number 1 seeds, at which point you can select randomly.
Before someone jumps to the comments higher ranked team It's worth noting that you could enhance your strategy further by checking the current betting odds for the games. For example, when two number 1 seeds compete against each other, diving into offshore Las Vegas odds would provide insight into which team has the upper hand, but I won’t delve into that here.
The focus of this video will strictly be on selecting the higher-seeded team throughout, and when you arrive at the final four number 1 seeds, you can just pick randomly. Alright, I've finished with my introduction.
I want to apologize upfront for using a tablet in the next section of this video. I've encountered several technical difficulties getting everything to function properly, which is why I opted for this format for my introduction. So, without further ado, let’s discuss how to calculate the odds of a perfect March Madness bracket based on my aforementioned strategy.
This video marks my first attempt at using a creative pen tablet, if that's the right term. I've always wanted to create educational videos similar to those of Khan Academy, but centered around gambling and mathematics. Now that the introduction is complete, let’s jump straight into the calculations.
Based on my assessment, the chance of a number 1 seed defeating a 16 seed is approximately 135 out of 136, as historically there have been 136 matchups, with the number 1 seed emerging victorious 135 times. Thus, the probability of a 1 seed winning any given game is about 99.26%.
All right, here we go:
Since there are four divisions, you need to calculate this probability four times, which means raising it to the power of four.
Additionally, there are four matchups where a number 2 seed faces a 15 seed. Over the course of the 136 instances of this matchup, the number 2 seed has won 127 times, translating to a historical probability of 93.38% for a 2 seed to triumph over a 15 seed. This calculation also applies to all four divisions.
However..
Similarly, the odds of a 3 seed defeating a 14 seed stands at 115 out of 136, and this must be calculated four times as well. The probability for a 4 seed defeating a 13 seed is 108 divided by 136, requiring the same four-time calculation due to the four games to win.
A 5 seed's chances of beating a 12 seed is 89 out of 136, corresponding to approximately 65.44%, and again, this extends to the fourth power. A 6 seed against an 11 seed has a win-rate of 85 in 136, which equates to 62.5%. For a 7 seed versus a 10 seed, the win total is 83 out of 136, making the win probability 61.03%. Lastly, the odds of an 8 seed triumphing over a 9 seed is 71 out of 136, and you’ll also be applying this to four separate calculations.

..after which, you will successfully advance past the first round. In the second round, number 1 seeds will face off against number 8 seeds. This matchup has occurred 72 times, and out of those, the number 1 seed has won 58 times. Therefore, the probability of a 1 seed winning against an 8 seed is 80.56%, which must also be factored for all four divisions.
Next, number 4 seeds will compete against number 5 seeds. This has happened 73 times historically, with the 4 seed winning 41 of those, which gives a probability of 56.16% for each game. Taking into account the four divisions, this will again be taken to the fourth power.
If you win all of these games..
Following this, number 3 seeds will match up with number 6 seeds. The 3 seeds have emerged victorious 41 out of 70 times, resulting in a probability of 58.57% per game. Finally, progressing to round two, number 2 seeds will contest against number 7 seeds, with the 2 seed winning 56 times out of 79, leading to a win probability of 70.89%. Assuming all these victories are achieved, you will continue to round three where the 1 seeds face the 4 seeds.
Historically, this matchup has occurred 61 times , with the number 1 seed winning 44 times, equating to a win probability of 72.13% for each game. In the next round, the 2 seeds will face the 3 seeds, which has taken place 52 times, resulting in a 32 win count for the 2 seed. This probability still needs to be applied across four different divisions.
Given that you succeed in all those matchups:
You will be left with only number 1 seeds and number 2 seeds. The odds of a 1 seed defeating a 2 seed is 35 out of 64, based on the historical data, again requiring this calculation to span all four divisions.
If you've reached this stage.. you will have retained
, with the top-ranked team prevailing each time. At this point, you start to make random picks. You will need to win three more games to determine the best among these four teams, and as I mentioned earlier, you just make random selections, which gives you a likelihood of winning each time as 1 in 2 across three additional games.
This represents your winning probability based on my strategy , culminating in a calculation of 1 in 42,743,890,552. Therefore, I consider this to be the most precise estimate for filling out a perfect March Madness bracket. won all four divisions As I mentioned earlier, you can fine-tune your approach by reviewing current betting odds, and I genuinely appreciate you taking the time to watch this video. I understand that it may not have been particularly engaging.
Think of this as a valuable learning opportunity for me, and once again, all the information discussed can be found in writing on my website.
Look for the sports betting section to locate the page dedicated to completing a flawless March Madness bracket. I believe that covers everything.
Accurate strategic advice and insights for various casino games, including blackjack, craps, roulette, and countless others. internetradiomercedes.com Please check your email for the link we sent, and follow it to finish registering.
So thank you for watching.


