Understanding the Odds in Five Card Stud Poker
Hello everyone, I’m Mike, and today I’ll guide you on how to figure out the odds in five-card stud poker. To put it simply, I aim to help you grasp the chances of creating various poker hands from a random selection of five cards drawn from a total of 52. Before diving into the calculation of how many different combinations yield specific poker hands, let’s start with an easier inquiry. If you already know how to solve it, feel free to fast forward.
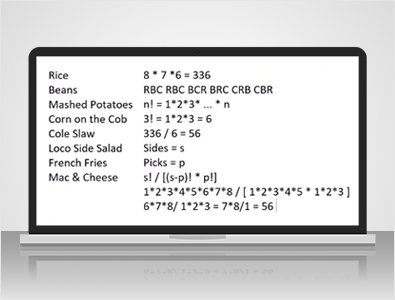
In El Pollo Loco:
There are eight classic side dishes listed on the left. While they do offer some premium options, I won’t delve into those to keep it straightforward. When you purchase the 12-piece meal, you’ll have the option to select any three out of these eight sides. For the sake of this example, let’s assume you must choose three distinct items.
The question is..
..how many different combinations exist for selecting three unique sides from eight? Imagine visiting this place daily and each time ordering three different sides. How long could you go before repeating the same combination?
If the sequence in which you ordered them mattered, you would calculate it as 8 x 7 x 6, since you have eight choices for your first item, seven for the second, and six for the third. However, the cashier isn’t concerned about the order.
If you say -
"I’d like rice, beans, and corn,\" your order remains the same whether you phrase it as \"rice, beans, and corn\" or \"corn, beans, and rice.\" So, how many different combinations can you create with three sides? Using rice, beans, and corn as examples, you could say them in various arrangements: rice first, beans second, corn last, or switch the order around – that gives you six different arrangements.
How did I arrive at the number six without jotting down each possibility?
Well, there’s a very simple formula If there are N items, the total arrangements you can create out of them is calculated as 1 x 2 x 3 all the way up to N.
In this instance, our question is about determining how many ways there are to arrange three items. The answer is 3!, calculated as 1 x 2 x 3, which totals 6. Considering there are 336 ways to arrange three items from among eight, when you take into account the ordering, you divide by six (the number of arrangements for every combination), leaving you with 56.
What’s the overarching formula, you might be curious about?
Assuming the number of sides is represented by S, and the number of selections allowed is P, the general formula for choosing P items from S is S! / (S - P)! x P!. Let’s work through this with the example presented.
In this case:
Given that S is 8, we find that 8! equals 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, and for the denominator, we calculate S - P, leading to 5! (since 8 - 3 equals 5). Therefore, 1 x 2 x 3 x 4 x 5, along with P! which is 3! equaling 1 x 2 x 3. You can see that 1 x 2 x 3 x 4 x 5 equals 120 in the numerator and denominator, which we can then simplify, resulting in 6 x 7 x 8 divided by 1 x 2 x 3. Simplifying further, using 2 x 3 = 6 gives us 7 x 8, which simplifies to 56.
We’re left with just..
For this session, I’d like to introduce a function notation. We’ll denote the function C(x, y) as the method for determining the number of ways to select y items from x, commonly referred to in mathematical terms as \"x choose y,\" expressed as x! / (x - y)! x y!.

In relation to the El Pollo Loco example, if we posed the question:
"In how many ways can you select three sides from eight?\"
We would phrase it this way, equating to 56. Now we can transition to discussing poker. How many different ways can you draw five cards from a total of 52? This is represented by 52 choose 5, calculated as 52! / 47!, where 47 results from (52 - 5) x 5! and this totals 2,598,960. Let’s begin with the royal flush.
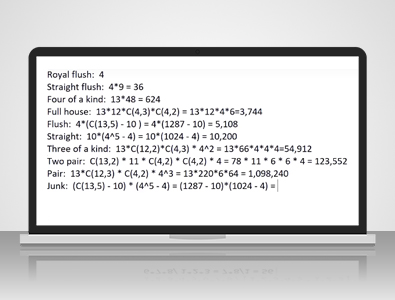
This one is simple as there are four suits for the royal flush: hearts, spades, clubs, and diamonds. The required ranks are ten, jack, queen, king, and ace. Hence, there are only four possible combinations: a royal flush of hearts, diamonds, clubs, or spades.
How about a straight flush?
Additionally, the straight flush is a bit more complex; it can start from the lowest rank of an ace ranging through to a nine, where ‘the wheel’ is an ace, two, three, four, and five straight flush and it ends at a nine, ten, jack, queen, and king. If we begin the straight with ten, jack, queen, king, and ace, that qualifies as a royal flush. Therefore, the lowest card can be anywhere from an ace to a nine.
In this case..
..the ace can be treated as one. This means there are nine potential sequences for the straight flush, leading to 4 suits times 9 spans, equating to 36.
For the full house
For four of a kind hands, you have 13 possible ranks, such as queens, followed by 48 remaining cards that are left for the other singleton after setting aside the four of a kind cards, which totals 624.
For three of a kind hands, there are also 13 ranks to select from, with 12 ranks remaining for the pair. For determining the three of a kind, it's a matter of choosing three suits from the four available, and for the pair, we pick two suits also from the four available. The overall calculation results in 13 x 12 x 4 x 6, which equals 3,744. With flush hands, we again consider the four suits.
How many combinations exist for selecting five ranks from the 13 within the same suit?
How about a straight?
This would be represented as 13 choose 5, though 10 of those combinations would yield either a straight flush or a royal flush. For instance, choosing ranks 5, 6, 7, 8, and 9 would form a straight flush, so we need to dismiss those 10 sets that consist of consecutive ranks. Following that, we calculate 13 choose 5 yielding 1,287, and after removing the 10 outcomes that lead to straights, and multiplying by 4, we arrive at 5,108.
How about a three of a kind?
As we discussed about flushes, there are indeed 10 different spans available for straights, starting from Ace two three four five extending to ten jack queen king ace. For each card within those ranks, there are four possible suits. Thus, the total ways to select varying suits for five cards becomes 4 x 4 x 4 x 4 x 4 = 4^5. In instances where all five cards share the same suit, those correspond to straight flushes or royal flushes. This necessitates subtracting those possibilities: 4^5 = 1,024 minus the 4 leads to 10,200 ways to produce a straight.
In calculating for three of a kind, you have 13 possibilities for the rank, then select two ranks from the remaining 12 for the two singletons. Upon doing so, you must then choose four suits for the three of a kind and one suit among four for each of the two singletons.
How about a two pair?
We conclude with 13 potential ranks for the three of a kind, and then 66 combinations for picking two ranks from the remaining 12 for the two singletons, multiplied by four choices for the three suits of the three of a kind, plus another four for the two singletons, resulting in a total of 54,912.
For the pair
For two pairs, there are 13 choose two methods to select two ranks from the available ranks for the two pairs, leaving one rank for the singleton. For each pair, you can choose two suits from the available four, and there are four options for the singleton suit. Therefore, 13 choose two gives us 78, multiplied by six, six, and four equals-- I neglect to add the 11 ranks available for the singleton. Finally, the calculation is 78 x 11 x 6 x 6 x 4 = 123,552.
Finally
You can choose 13 ranks for the single pair, and for the three singletons, select three ranks from the remaining 12. For the pair, the number of combinations is determined by choosing two suits from four, while for each singleton, there are four choices, culminating in 4 x 4 x 4 for the three singletons which equals 13 x 12 x (12 choose 3 which gives 220) x 6 x 4^3 equaling 64 = 1,098,240.
You take four to the fifth power..
Now let’s consider the chances of drawing an Ace or lower, commonly referred to as junk. To classify as junk, you would need five distinct ranks from the 13 available. The methods available to choose five ranks yield 13 choose five, but we again need to exclude the 10 sequences that would create a straight. After selecting your five non-consecutive ranks, each rank offers four suit options.
Next
..and similarly, as previously noted in the straights, we should deduct the four options that would yield a flush, leaving us with a total of 13 choose five equaling 1,287, subtract the 10 for the straights times 4 raised to the power of 5 equals 1,024 minus 4 amounts to a total of 1,302,540.
Let's compile this data into a spreadsheet. I’ll demonstrate how to execute this in Excel. We previously established that there's only four distinct methods to obtain a royal flush, with one available for each suit, 36 straight flush combinations derived from four suits multiplied by nine spans. For four of a kind hands, there are 13 ranks to choose from for the four of a kind and 48 remaining cards available for the singleton. For figuring out full houses, you can choose from 13 ranks for three of a kind and 12 for the pair.
For the flush
A four choose three calculation determines the suit combinations for the three of a kind, and for the pair, four choose two combinations must indicate two suits out of the four. The formula for Excel reflects this common function expressed in big number, small number format, just as I represented it earlier. This formula yields the previously calculated 3,744.

For the three of a kinds
You have four options for suits, and 13 choose five for selecting ranks from those suits, subtracting out the 10 consecutive spans that would result either in straight or royal flush combinations. This leaves us with 5,108 flushes. For straight calculations, there are 10 potential spans with four suits for each card in those spans, but again subtracting the four suits leaves you with combinations that result in straight flushes or royal flushes yielding a total of 10,200.
For three of a kind hands, with 13 ranks available, select two ranks from the remaining 12 for your two singletons. You can utilize four choose three for the three suits of the three of a kind and four options for each of the ranks chosen for the two singletons, resulting in a total of 554,912 combinations for three of a kinds. As for two pair hands, there are 13 choose two methods to choose two pairs’ ranks from the available options, leaving one rank for the singleton, involving choosing pairs in combinations of suits while also considering options for singleton ranks.
Finally, for the junk
Understanding the Odds in Five Card Stud Poker
One of the hundreds of casino games Find the Top Online Casinos Within Your Region Let it ride .
Calculator for Lottery Jackpot Ticket Sales
You can see..
Exciting Slot Tournaments with Huge Prize Pools
Hello everyone, I'm Mike, and in this video, I'll guide you through the process of figuring out the
For example, there is:
odds encountered in five-card stud poker
. Essentially, we're looking to determine how likely it is to get a specific poker hand when dealt five random cards from a standard deck of 52. Rather than jumping into the calculation of combinations for each type of poker hand immediately, let me pose a more straightforward question, and if you’re already familiar with the solution, feel free to fast forward.
The way I would express that..
..is the house advantage They offer eight well-known side dishes, which I've highlighted to the left. There are also some premium options available, but I won't complicate things by including them. If you decide to order a meal with 12 pieces, you can select any three from these eight sides. For the sake of the example, let’s assume you must choose three distinct items.
Thank you for watching.


