Analyzing Pair Square - A Side Bet in Blackjack

Hello everyone, I’m Mike. In this video, I will guide you through the process of calculating the return to player for the Pair Square side bet in Blackjack Before delving into the concept of 'Bet the Set', or Pair Square, I want to clarify a few mathematical functions that might already be familiar to you. The term 'n factorial' represents the number of distinct arrangements for n unique items.

It is simply the result of multiplying every whole number from one through n .

For example:

For instance, the calculation of five factorial illustrates how many different ways you can arrange five unique items, which is calculated as 1×2×3×4×5, resulting in 120. Additionally, let’s discuss combinations: this function tells you how many ways you can select Y items from X, in this case, without considering the order.

For example, think about selecting three unique side dishes out of eight available choices at El Pollo Loco.

This function..

..which can be expressed as X factorial divided by Y factorial, and then further divided by X minus Y factorial. I elaborated on the reasoning behind this in my video about probabilities in poker. A relevant example here is determining how many ways you can select five cards from a standard deck of 52?

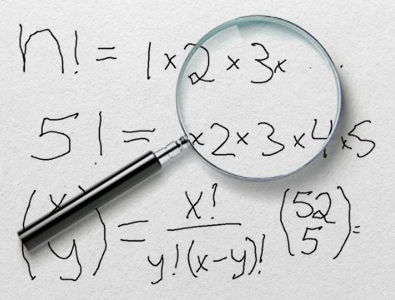
This equates to 52 factorial divided by five factorial and 47 factorial, yielding a total of 2,598,960 combinations. With this overview out of the way, let’s transition to the second part, where I will determine the combinations for every potential outcome of the Pair Square bet.

Ready to move on to the next step:

My aim here is to figure out how many combinations exist for each possible outcome associated with this wager. This is the main focus of this video . Assuming we have six card decks, we must acknowledge that there are 52 possible cards available in the play area. 13 ranks multiplied by four suits gives us the total of 52 cards, both cards must match.

For example, both cards could be the five of diamonds. After selecting your specific card, you will find six copies of that card in the deck. six-deck shoe .

You need to choose two out of those six available cards. The result of choosing two from six is 15, so when you multiply 52 by 15, you arrive at a total of 780. Thus, there are 780 different combinations for achieving the suited pair win. Now, what about the unsuited pair? Initially, you need to select the rank for your unsuited pair, let’s say fives.

Next, you must select two distinct suits for this pair, ensuring they are different. If both were of the same suit, you'd have a suited pair, which would yield a higher payout.

You can choose two suits from four available options, which mathematically is represented as four choose two, resulting in six. After determining the rank and the two chosen suits, you then have six options to select each card from the six decks.

For example:

If, for example, your two cards are the King of Clubs and King of Spades, you would find six of each in the shoe. The equation 13 multiplied by six multiplied by six squared calculates to 2,808. Ultimately, the way to lose this bet is simply by not obtaining a pair.

How many ways can you not get a pair?

To achieve this, you must select two different ranks from the 13 available, for instance, sevens and tens. After selecting your two specific ranks, each of those ranks has a total of 24 cards throughout the shoe.

Each deck contains four cards of any given rank, and since we have six decks in total, this amounts to 24 cards per rank—like 24 aces, for instance. If you choose aces and kings, you again have 24 of each.

You pick one out of each of those groups.

The calculation entails 13 choose two, which equals 78, and multiplying that by 24 squared leads to 44,928—and there we have our combinations. Now, let’s take all this information and transfer it into Excel to evaluate the value of the Pair Square bet.

Let's go on to the final part of this..

I just demonstrated how to calculate the number of combinations for every possible outcome in the Pair Square wager. In most cases, with six decks, the common payout structure awards 15 to one for a suited pair and 10 to one for an unsuited pair.

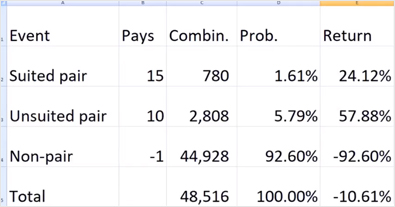
Now, let’s work out the probability for each scenario - this is actually quite straightforward. The chance of obtaining a suited pair is figured by dividing the number of ways to form a suited pair by the total possibilities of drawing two cards out of the 312 in the shoe, which totals to 40,516. So, 780 divided by 40,516 gives us approximately 1.61%.

Applying the same formula for calculating the odds of each event provides us with other probabilities: a 5.79% chance for an unsuited pair and a 92.6% probability for drawing two different ranks.

Next..

..personally, I prefer to assess a wager by simply multiplying the win amount by its probability. For the suited pair, the return is calculated as 15 multiplied by the probability of drawing one, 1.61%, resulting in about-- Let’s enlarge that for better visibility: 24.12%. Using similar calculations, we derive that the return from an unsuited pair stands at 57.88%, while the return from a non-pair shows a negative return of 92.6%.

This essentially means that if a player bets a dollar

For instance: he can anticipate recovering 24.12 cents from his suited pairs, 57.8 cents from his unsuited pairs, but will lose 92.6 cents when he does not hit a pair. To aggregate these values, simply add them together to get an overall loss of negative 10.61%. value to the player Hence, the player can expect to lose 10.61% of the total amount wagered on the Pair Square bet. In another way, this translates to a house advantage of 10.61%. This implies that for every dollar staked, the player may expect to get back roughly 89.39 cents, while 10.61 cents goes to the house.

That means..

In standard blackjack, the house edge can be as low as 0.28%. Even under unfavorable conditions, it typically sits closer to 0.6%. When you consider this significant house advantage, nearly 11%, it starkly contrasts with the nearly 1% you'd find in typical blackjack chances assuming optimal payout conditions.

To put this in perspective: the house advantage This reinforces my long-held belief that

are ultimately losing bets. This is a quintessential illustration of that concept. I highly recommend steering clear of this side bet and any other similar bets whenever possible. side bets Thank you for tuning in, and I look forward to seeing you in my next video.

Correct mathematical strategies and insights are vital for games found in casinos such as blackjack, craps, roulette, and many more.

Written by: Michael Shackleford