Round Robin Scheduling

This week's discussion focuses on organizing a round robin tournament. To clarify, a round robin format means that each participant competes against all other participants. In a setup involving n competitors, the total matches required will be calculated as n(n-1)/2.

It might seem straightforward to enumerate all n(n-1)/2 potential matchups among n competitors. However, the preferred approach is to arrange them into rounds, where every player competes once in each round. For instance, let’s explore this with a scenario involving eight players. In the accompanying image, we label the competitors A through H, and the rectangles display the pairings for four matches. These represent the initial round of play. Notice how each individual gets a chance to participate.

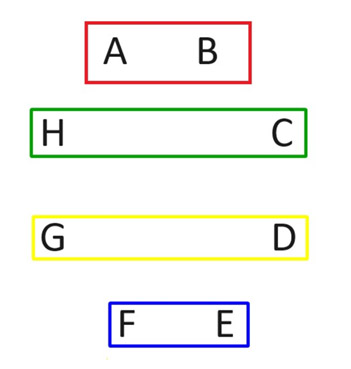
During the second round, maintain player A's position. Then, rotate the other participants in a clockwise manner as depicted in the next diagram.

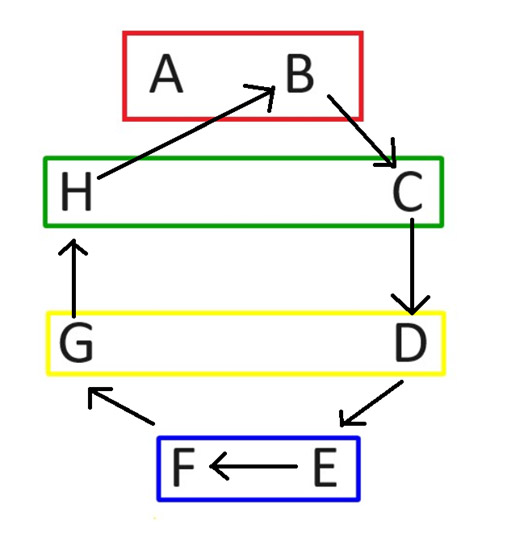
Following the rotation, the matchups for the second round will be arranged as shown below:

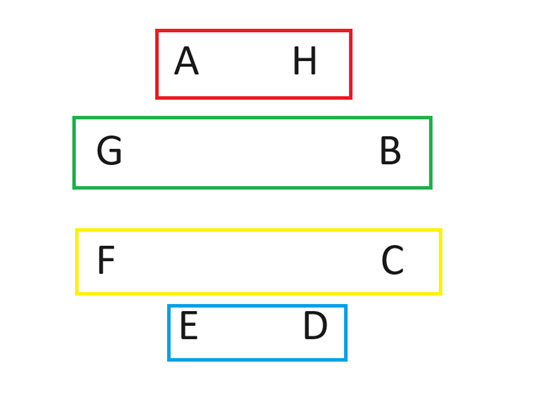
Keep rotating the positions until every player has faced player A. Although I can’t fully explain the logic behind this method, it has been proven effective for any even number of participants. If you seek more on this subject, look up terms like “circle method” and “round robin.”

The table below displays all matchups for the scenario involving eight players. Take note that each person competes against every other person exactly one time.

Round	Player 1	Player 2
1	A	B
1	H	C
1	G	D
1	F	E
1	A	H
2	G	B
2	F	C
2	E	D
3	A	G
3	F	H
3	E	B
3	D	C
4	A	F
4	E	G
4	D	H
4	C	B
5	A	E
5	D	F
5	C	G
5	B	H
6	A	D
6	C	E
6	B	F
6	H	G
7	A	C
7	B	D
7	H	E
7	G	F

In situations with an odd number of participants, simply introduce a dummy player to make the total even. The player matched against the dummy will receive a bye that round, meaning they won’t compete. This results in each participant having one round where they do not play. Here’s how this approach applies in a tournament with seven players.

Round	Player 1	Player 2
1	A	B
1	bye	C
1	G	D
1	F	E
2	A	bye
2	G	B
2	F	C
2	E	D
3	A	G
3	F	bye
3	E	B
3	D	C
4	A	F
4	E	G
4	D	bye
4	C	B
5	A	E
5	D	F
5	C	G
5	B	bye
6	A	D
6	C	E
6	B	F
6	bye	G
7	A	C
7	B	D
7	bye	E
7	G	F

Now, let’s consider a tennis tournament situation where each court has a favorable and unfavorable side. The unfavorable side might, for example, face directly towards the sun. What would be a fair method to ensure that every competitor experiences both the good and bad sides an equal number of times?

To address this dilemma, I propose employing the method of rock-paper-scissors, similar to what is suggested in the Big Bang Theory. This approach is effective for any odd quantity of symbols. To justly decide which participant gets the advantageous side, let’s analyze the seven-player scenario. The diagram below illustrates which player receives the good side, indicated by the arrow pointing towards the player designated the bad side. Lizard Spock Expansion As an illustration, if players B and D face off, player B would enjoy the favorable side because the arrow indicates towards player D. The method used to create this diagram is evident; arrows consistently flow in a clockwise direction. It's essential to illustrate these for every potential number of gaps ranging from 1 to 3.

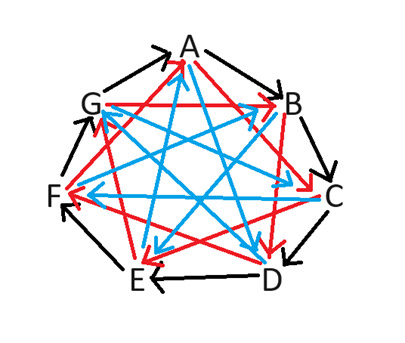
That said, constructing such a diagram is not necessary; a simple ring of letters would suffice. Evaluate both directions around the circle to determine the shortest path between players. The route requiring fewer steps yields the player who gets the good side. For example, in a match between B and F, moving clockwise requires four steps from B to reach F, while from F to B it only takes three steps. Since three steps are fewer than four, player F receives the advantageous side.

The following table outlines all possible matchups in a seven-player round robin, indicating which players secure the advantageous and disadvantageous sides.

Regrettably, this method for balancing sides does not translate effectively when dealing with an even number of participants. This limitation arises because the distances between two players becomes equal when they are directly opposite each other on the circle. Although forced adaptations of this method could be employed for other matchups, it would require players to randomize their outcomes when positioned 180 degrees apart on the circle.

Round	Good side	Bad side
1	A	B
1	C	bye
1	D	G
1	E	F
2	A	bye
2	G	B
2	C	F
2	D	E
3	G	A
3	F	bye
3	B	E
3	C	D
4	F	A
4	E	G
4	D	bye
4	B	C
5	E	A
5	D	F
5	G	C
5	B	bye
6	A	D
6	C	E
6	F	B
6	G	bye
7	A	C
7	B	D
7	E	bye
7	F	G

That's about all I'd like to cover on this topic for the moment. I retain the option to expand upon it in future newsletters. Other potential topics could delve into matches involving three or more participants, or the organization of multiple courts ensuring each player has fair playtime on each.

To conclude, I wish everyone a joyful Hanukkah!

Accurate mathematical strategies and insights for casino games such as blackjack, craps, roulette, and countless others.

Written by: Michael Shackleford