March Madness 2025

Logic Puzzle

Before diving into this week's discussion on statistics from March Madness, let's take a moment for our regular weekly brain teaser. Here it is.

In a game involving three players, three coins are flipped without the players' knowledge, one for each. Depending on how each coin lands, players are blindfolded and subsequently given either a black or a white hat. Once the blindfolds are removed, each player can see the hats worn by the other two, but they cannot see their own.

Each participant is then presented with a private voting slip to indicate the color of their hat. They have the options of choosing black, white, or passing. For the outcome of this activity to be deemed successful, all players who choose to vote must be correct in their selection of white or black. However, if all three individuals opt to “pass”, the attempt is considered a failure.

The players have some time to plan their moves. What tactics can they adopt to achieve a 75% success rate?

March Madness Update

In the past, I used to wager quite frequently on proposition bets during March Madness. A common scenario might involve betting on the over/under for the total games won by teams in the Pacific 12 conference. Knowing the winning potential of different seeds was crucial for evaluating such bets.

Some wagers are settled in the opening round, especially concerning whether a seed rated 13 or lower will win a game. Here are some instances from Covers relevant to this year.

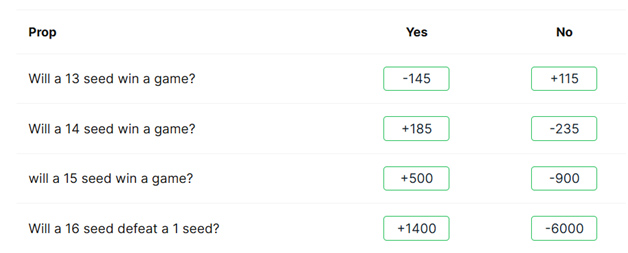
This year, the lowest seed that managed to win was ranked 12th. Consequently, none of the earlier mentioned bets would have been successful.

The subsequent table details the odds of any given seed winning a first-round game as well as the likelihood for any of the four teams within that seed category. This data spans the 40 years of NCAA tournaments from 1985 through 2025.

Seed	Specific Team Wins	Any Team Wins First Round
1	98.75%	100.00%
2	92.50%	100.00%
3	85.63%	99.96%
4	79.38%	99.82%
5	64.38%	98.39%
6	61.25%	97.75%
7	61.25%	97.75%
8	50.00%	93.75%
9	50.00%	93.75%
10	38.75%	85.93%
11	38.75%	85.93%
12	35.63%	82.83%
13	20.63%	60.31%
14	14.38%	46.25%
15	7.50%	26.79%
16	1.25%	4.91%

This season, the average seed advancing past the first round was 5.34, while the overall tournament mean stands at 5.84.

Moving to the second round, the average seed reaching the Sweet Sixteen was 3.44, with the overall tournament average at 4.52. The lowest-ranked seed that managed to progress past two games was 10, indicating that underdogs fared poorly this year in the initial rounds.

In the third round leading to the Elite Eight, the average seed making it this far was 1.625, contrasting with an average of 3.30 across the tournament. The lowest seed to make it through three matches was ranked 3, of which there was only one instance. This equals a tournament record for the lowest seed to survive to this stage, a feat that has also occurred in 2007 and 2009. The average surviving seed number of 1.625 marks a historic low.

In the Final Four scenario, all participating teams were ranked number 1. This uniqueness had previously occurred only once, in the 2008 tournament. There exists a popular proposition bet regarding the exact number of One Seeds that will reach the Final Four, with this year’s specifics provided by Covers.

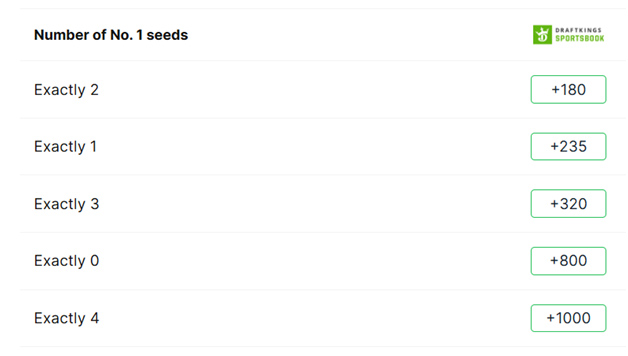
The forthcoming table illustrates how many Number One seeds have reached the Final Four throughout 40 years of the tournament.

#1 Seeds	Count	Probability
4	2	5.00%
3	4	10.00%
2	15	37.50%
1	16	40.00%
0	3	7.50%
Total	40	100.00%

The odds of any particular Number One seed making it to the Final Four stand at 41.25%.

It's obvious that with all four teams in the Final Four being Number One seeds, it would follow that at least two of these would also reach and win the Championship Game.

A different proposition bet involves which seed will ultimately win the Championship Game. Here are the relevant Covers bets for this year.

The following table illustrates the frequency of each seed's victory in the Championship Game.

Winning Seed	Count	Probability
1	26	65.00%
2	5	12.50%
3	4	10.00%
4	2	5.00%
5	0	0.00%
6	1	2.50%
7	1	2.50%
8	1	2.50%
9 to 16	0	0.00%
Total	40	100.00%

Returning to our analysis of expected wins by seed, here is a revised table incorporating data from the current season.

Seed	Average wins
1	3.34
2	2.33
3	1.84
4	1.56
5	1.14
6	1.06
7	0.89
8	0.73
9	0.59
10	0.61
11	0.64
12	0.51
13	0.24
14	0.16
15	0.11
16	0.01

A common inquiry I receive pertains to the likelihood of achieving a perfect bracket. By adhering to a strategy that involves consistently choosing the higher-seeded player (or the lower number) unless faced with a direct match-up, my updated probability, reflecting this season's data, is 1 in 287,548,153.

Logic Puzzle Answer

The strategy should be as follows:

1. • If you observe two hats in different colors, it’s best to pass.
2. • If you detect two hats of the same color, select the opposite color.

Based on the outcomes we can anticipate according to these three colors:

1. • If there are three black hats: All players will witness two black hats and cast a vote for white. Everyone will be incorrect, leading to a failure of the experiment.
2. • If two hats are black and one is white: The player wearing the white hat will see two black ones and will correctly choose white. The players with the black hats will see one of each color and thus pass. The experiment succeeds.
3. • If there is one black hat and two white hats: The black-hatted player will observe two white hats and vote for black. The two white-hatted players will then see one of each and pass, leading to a successful experiment.
4. • With three white hats: All players will see two whites and vote for black. Everyone will be incorrect, resulting in a failed experiment.

The combined chances of getting three hats being either all white or all black is 2*(1/2) = 25%. Conversely, the likelihood of having a 2-1 split between the two colors stands at 75%. As outlined previously, in the case of a 2-1 division, the experiment is projected to succeed.³Theoretical strategies and essential insights for playing casino games like blackjack, craps, roulette, and countless others are available.