Price is Right Contestants Row
Before diving into the main discussion, here’s a quick update. Recently, I wrote about how to acquire tickets for Burning Man. Last Wednesday, I took my shot at the Main Sale. If you remember, the final step was to be prepared to purchase tickets precisely at noon on March 30. I was fully prepared, with three web browsers open, all linked to the sale. To be honest, I’m not convinced this strategy improved my chances, but many insiders on Burning Man suggest this approach.
In summary, I was unable to secure a ticket. I expected this outcome. At least I made the attempt. Unlike back in 2019, the notification on my screen was updated about half an hour post-sale start, indicating that tickets had sold out. You might wonder if I clicked the 'back' button, which the message indicated would be futile. I chose not to do so.
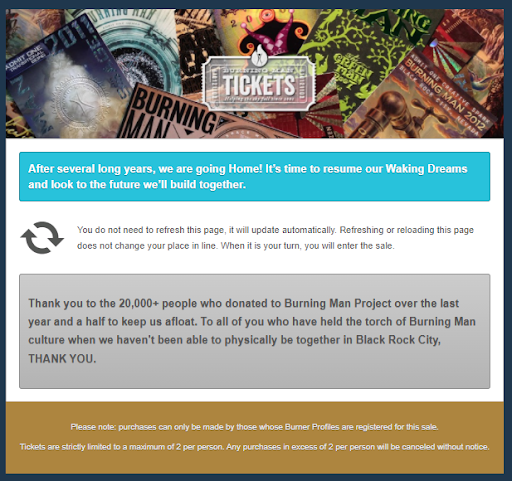
It seems that attending Burning Man this year is not in the cards for me. That’s alright, as I have several other exciting vacation plans.
Now, let’s shift gears and discuss Contestants Row on The Price is Right. This segment is featured six times during each episode. For those unfamiliar with the game, here’s how it works:
- Four contestants are selected to vie for the next pricing game.
- A specific item is presented, typically valued between $1,000 and $2,000. For instance, it might be a high-quality bicycle.
- The contestants, following a set sequence, will place their bids regarding the item's value.
- The contestant whose bid is closest to the actual price without going over wins the item and gets the opportunity to play the next pricing game.
- If all contestants exceed the actual price, they will rebid in the same order, instructed not to exceed the lowest bid from the prior round. This continues until at least one player makes a valid bid.

What strategy should you adopt in this game, especially if you're unfamiliar with the item's worth?
Many contestants lack effective strategies. Imagine you’re the last to bid and the previous bids were $1,500, $1,600, and $2,400. Knowing nothing about the item’s value, ideal bids would be:
- $1: This captures a range up to $1499 - essentially covering values from $1 to $1499, although prizes are rarely this low.
- $1601: This covers an $800 range – values from $1,600 to $2,399.
- $2401: This encompasses an indefinite range – covering values from $2,400 upwards indefinitely.
It's common to see players making bids that unnecessarily limit their potential range. For example, a bid of $2000 unnecessarily forfeits the range from $1600 to $1999, in contrast to bidding $1600, which retains that range.
There's no single winning strategy that applies to all situations. Focus on covering the widest possible range, especially within typical prize values.
What if a quartet of logicians were competing, you might ask? Let's assume they're completely ignorant of the item's worth. To simplify this discussion, we’ll say they can make bids down to the penny.
Consider a straightforward scenario where the prize value is randomly selected from a uniform distribution ranging from $0 to $1000. Clearly, going last confers a significant advantage. I won’t delve into the complex math, but here are the bids the four logicians would make, listed in order from the first to the last:
- Player 1: $777.80
- Player 2: $555.57
- Player 3: $333.33
- Player 4: $0.01, $333.34, $555.57, or $777.79.
The crucial aspect is for the first three players to position the following players near an indifference point. Each aims to minimize the remaining bidding space without encouraging the next player to bid just a penny higher.
If they bid strategically this way, player 4 will hold a 33.3% chance of winning, irrespective of the bids I outlined for them. Meanwhile, each of the other players would have a 22.2% chance of victory. I’ve added a penny or two to the bids of players 1 and 2 to prevent players 3 and 4 from outbidding them by $0.01.
However, this example lacks realism since actual prize values tend to follow an exponential distribution. To make it more realistic, let’s assume the prize value is chosen randomly from an exponential distribution with a mean of $1,000.
Without diving into the math, here are the optimal bids based on the earlier assumptions:
- Player 1: $1,504.08
- Player 2: $810.98
- Player 3: $405.47
- Player 4: $0.01, $405.48, $810.99, or $1,504.09
The winning probabilities will mirror those from the previous situation, granting player 4 a 33.3% chance while all others receive 22.22%.
That concludes this week’s discussion. Until next time, may luck be on your side.


