How to apply the PEMDAS rule.

If you're anything like me, your social media feeds are filled with constant inquiries regarding the order of operations. Often, these questions spark lengthy discussions in the comments, where most responses are incorrect. Interestingly, no one ever seems to take responsibility for their mistakes.

What qualifies my perspective to be accurate? Firstly, I have established myself as an authority on the mathematics involved in casino gaming. A quick search on any casino-related game or term will reveal my contributions. In addition, I hold a degree in mathematics and economics from the University of California, Santa Barbara, and I am an honorary member of the Society of Actuaries. My career has consistently revolved around mathematical principles since my graduation.

An example of such a question is:

6 ÷ 2 (1 + 2) = ?

Pause for a moment and work it out.

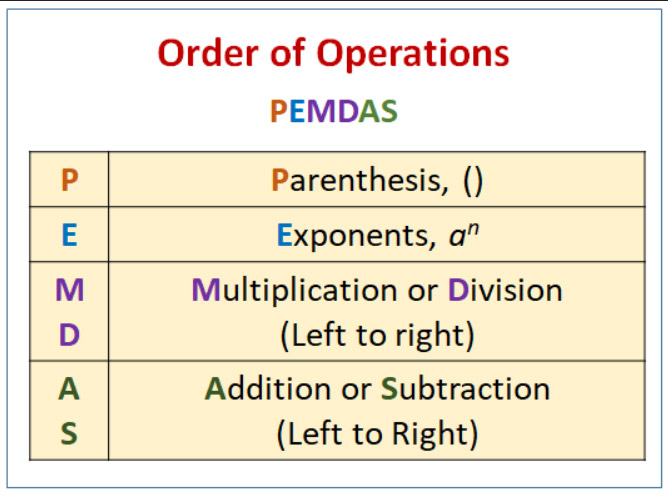
If your answer was 1, it's not correct. My suspicion that you're mistaken arises from your reliance on the PEMDAS mnemonic for the order of operations, a guideline usually introduced in the fifth grade. The acronym is often remembered with the phrase 'Please Excuse My Dear Aunt Sally' to help students recall the sequence in which to evaluate expressions:

1. 1. Parenthesis
2. 2. Exponents
3. 3. Multiplication
4. 4. Division
5. 5. Arithmetic
6. 6. Subtraction

Your elementary school instructor likely believed this rule was effective, yet it's not infallible. While its simplicity may make it suitable for young learners, the downsides of such simplifications can lead to incorrect conclusions, especially in nuanced situations like those involving PEMDAS. For example, solving the operation 6 ÷ 2 (1 + 2) might be tackled as follows:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) due to prioritizing operations within parentheses
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 because the absence of an operator outside of parentheses suggests multiplication
3. 6 ÷ 2 × 3 = 6 ÷ 6 since, according to PEMDAS, multiplication takes priority over division
4. 6 ÷ 6 = 1

The flaw in this reasoning appears at the third step. It's important to note that multiplication and division possess equal precedence. When both operations are present in an expression, prioritize the one that appears first from the left.

Additionally, it's worth mentioning that addition does not necessarily come before subtraction; they too share equal precedence. In these cases, where the rules don't dictate a clear order, it makes no difference which operation you choose to perform first.

Here is the correct way to evaluate 6 ÷ 2 (1 + 2):

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) due to prioritizing operations within parentheses
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 since having no operator outside the parentheses indicates multiplication
3. 6 ÷ 2 × 3 = 3 × 3 because when encountering multiplication and division together, evaluate from left to right
4. 3 × 3 = 9

Here is another question for you:

7 + 7 ÷ 7 + 7 × 7 – 7 = ?

On platforms like Facebook, you might see people arriving at the answer of 56. This common error arises not from misunderstanding PEMDAS, but rather from the statement, 'My calculator indicates the answer is 56.' This represents a careless and incorrect interpretation that results from simply moving leftwards across the equation. The flawed logic here is:

1. 7 + 7 ÷ 7 + 7 × 7 - 7 = 14 ÷ 7 + 7 × 7 - 7 because you simply work from left to right
2. 14 ÷ 7 + 7 × 7 - 7 = 2 + 7 × 7 - 7 because you continue evaluating from left to right
3. 2 + 7 × 7 - 7 = 9 × 7 - 7 because you keep evaluating in a left-to-right sequence
4. 9 × 7 - 7 = 63 - 7 as you maintain the left-to-right evaluation principle
5. 63 – 7 = 56

The appropriate method for solving this expression should be:

1. 7 + 7 ÷ 7 + 7 × 7 - 7 = 7 + 1 + 7 × 7 - 7 as division takes precedence over addition and occurs to the left of multiplication
2. 7 + 1 + 7 × 7 - 7 = 7 + 1 + 49 - 7 since multiplication takes precedence over both addition and subtraction
3. 7 + 1 + 49 - 7 = 8 + 49 - 7 because you must complete the leftmost operation before moving on to the next
4. 8 + 49 - 7 = 57 - 7 again following the rule of performing the leftmost operation first
5. 57 – 7 = 50

It's noteworthy that this example successfully adheres to PEMDAS. Many people miscalculate due to improper use of their calculators. Ensuring that numbers and operations are entered correctly is critical. This task is made significantly easier on calculators that utilize reverse Polish notation, like the HP15C. By the way, anyone who possesses an HP15C or 12C automatically earns my friendship.

In conclusion, I want to present my own twist on these order of operations challenges with a unique puzzle I created, featuring both engaging logic and a distinctive format. I acknowledge that the images I used were sourced from Google. This puzzle was inspired by a similarly challenging one from a Mind Your Decisions YouTube channel. Feel free to share it wherever you'd like; I'm hoping it gains popularity.

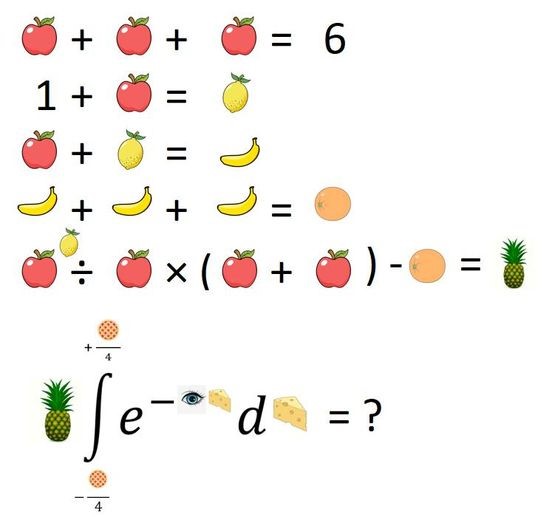
Partial credit will be awarded for only solving for the pineapple, while full marks will be given for resolving the integral.

I plan to share the solutions in the newsletter scheduled for June 29. Until then, may luck be on your side.

Written by: Michael Shackleford