Folded Rectangle Puzzle

In this edition of the newsletter, I've included a mathematical challenge derived from the Mensa Bulletin released in November.

Imagine you have a rectangle measuring 1x4. Now, if you fold it so that two opposite corners meet, it resembles the illustration provided.

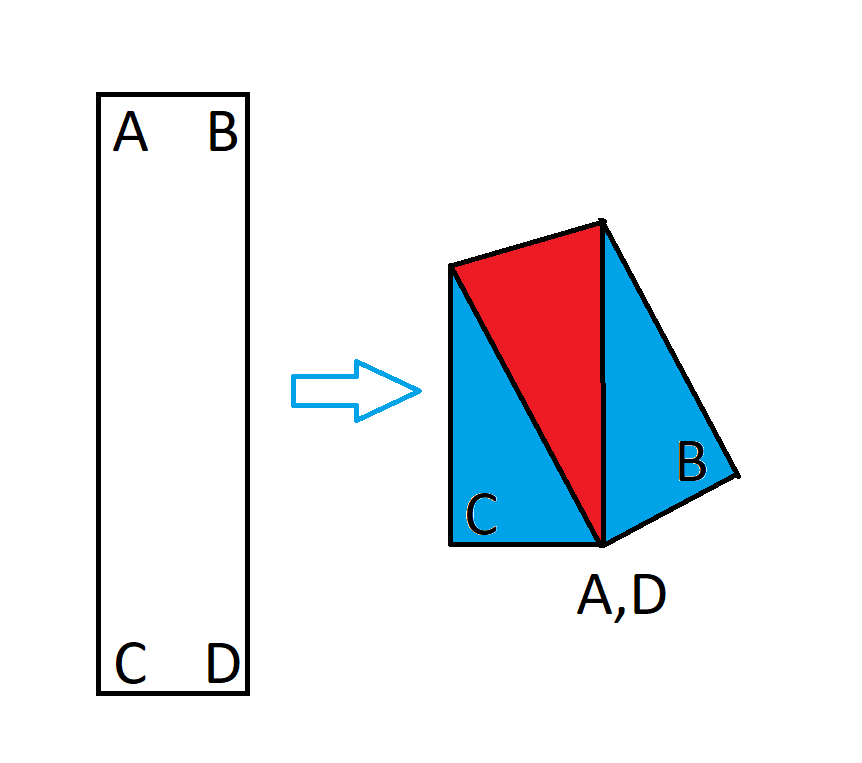
When the rectangle is folded in this manner, it transforms into an irregular pentagon. Your task is to find the ratio of the area where the paper overlaps to the overall area of the pentagon. Essentially, this means you need to compare the overlapping area marked in red in the diagram with the entire pentagon's area.

Continue reading below to find the solution and detailed explanation.

Answer

The answer is 17/47 = apx. 0.3617

Solution

To clarify the solution, I will introduce more key points as depicted in the next image. Point F represents the midpoint between points E and G.

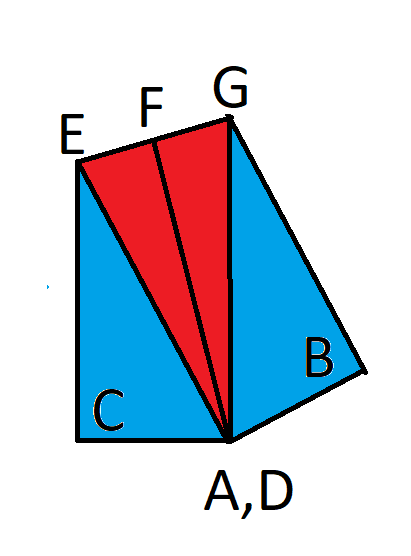
We know:

AC = 1

CE + AE = 4

Let's determine the length AE by applying the Pythagorean theorem:

1²+ (CE)²= (AE)²

Substituting 4 – CE for AE we get:

1²+ (CE)²= (4 – CE)²

1 + (CE)²= 16 – 8(CE) + (CE)²

8(CE) = 15

CE = 15/8

Going back to 1²+ (CE)²= (AE)², we can solve for (AE) since we know EC:

(AE)²= (CE)² + 1²

(AE)²= (15/8)² + 1²

(AE)²= 225/64 + 64/64

(AE)²= 289/64

AE = 17/8

Prior to folding, the distance between points A and D represented the diagonal of the rectangle. By using the Pythagorean formula again, we find this length to be sqrt(17).

(AF) is half that length, or sqrt(17)/2.

Having calculated AE and AF, we can find EF by again using the Pythagorean theorem:

(AE)²= (EF)²+ (AF)²

(17/8)²= (EF)²+ (sqrt(17)/2)²

289/64 = (EF)²+ 17/4

289/64 = (EF)²+ 272/64

(EF)²= 17/64

EF = sqrt(17)/8

As previously mentioned, F divides the segment EG equally. Thus, EG measures 2*sqrt(17)/8, simplifying to sqrt(17)/4.

The area of the red triangle AEG can be computed as (1/2) multiplied by the base multiplied by the height, which equals:

= (1/2) × sqrt(17/4) × sqrt(17)/2

= (1/2) × (17/8) = 17/16

Calculating the area of triangle ACE gives us (1/2) times the base times the height, resulting in:

(1/2) × 1 × (15/8) = 15/16.

The total area of the pentagon combines the areas of AEG and twice that of ACE, leading to:

(17/16) + 2*(15/16) = 47/16

Consequently, the ratio of the overlapping red area to the total area of the pentagon is:

(17/16) / (47/16) = 17/47 = apx. 0.3617

Folded Rectangle Puzzle 1x4 rectangle