Video Poker (Encrypted Version)

Introduction

This section discusses a video poker gameplay technique that utilizes encryption to guarantee predetermined card outcomes. If you're new to the fundamental rules of video poker, please refer to my primary page. video poker page.

Currently, my focus is on Cypto.Games. They offer three different variations of video poker, which are detailed as follows:

• Jacks or better
• Tens or better
• Bonus poker

A player is required to place a bet of 10 credits, though they have the flexibility to determine the equivalent value in Cryptocurrency. Personally, I believe that the step involving ten credits complicates the process unnecessarily.

CryptoSlots Casino

Users gave CryptoSlots Casino a rating of 4 out of 5 Stars

Sign Up Bonus

111% up to
$500

Exclusive Offer for New Customers. Terms and Conditions Apply. Must be 18 or older. Minimum deposit: $25. Eligible games: All (excluding Jackpot Trigger). Maximum withdrawal limit: $5,000.

Wizard Of Odds - Approved

PL Friendly

Visit Casino

New

Stake Casino

Users gave Stake Casino a rating of 4 out of 5 Stars

PL Friendly

Visit Casino

mBitCasino

Users rated mBitCasino at 3.9 out of 5 Stars

Sign Up Bonus

100% up to
₿1

+100 spins

This offer is valid only for new users. Terms and Conditions apply. Must be 18 or older. Minimum deposit: 0.000722 BTC, 0.013 ETH, 0.13 BCH, 0.42 LTC, 313 DOG, 30 USDT, and 50 XRP. Maximum Bet: 0.003 BTC / 0.55 LTC / 0.10 BCH / 0.12 ETH / 10660 DOGE / 28 USDT / 42 XRP. Additionally, receive 100 Free Spins on selected games such as Book of mBit, Elvis Frog in Vegas, and several others. The bonus is valid for 7 days, while the Free Spins are valid for 3 days.

Wizard Of Odds - Approved

PL Friendly

Visit Casino

CryptoWins Casino

Users gave CryptoWins Casino a rating of 3.4 out of 5 Stars

Sign up Bonus

77% up to
₿1

New User Offer. Terms and Conditions Apply. Must be 18+. This promotion is not applicable for players located in Ontario. New User Offer. Terms and Conditions Apply. Must be 19+. Minimum deposit: $5. Maximum cash out: $30,000. This applies to select games only; visit the website for a list of available online slots. Bonuses must be played through within 10 days.

PL Friendly

Visit Casino

Analysis

The table below presents my evaluation of the 6-9-20-75-500 Jacks or Better payout structure. The bottom-right cell indicates a return rate of 97.97%, which corresponds to a house edge of 2.03%.

The table below shows my evaluation of the 5-6-22-75-500 Tens or Better payout structure. The bottom-right cell reflects a return rate of 97.97%, translating to a house edge of 2.03%.

The table below summarizes my assessment of the 5-8-25-35-75-45-500 Bonus Poker payout structure. The bottom-right cell indicates a return of 97.94%, resulting in a house edge of 2.06%.

Fair Gaming

This specific iteration of video poker appears to be available solely through cryptocurrency online casinos. In a nutshell, the game selects ten distinct random numbers ranging from 0 to 51, each having a probability of 1 out of 52, and assigns them to ten cards from the deck. The first five numbers determine the initial five cards dealt to the player, and the subsequent five dictate the cards the player will receive in the draw order. For instance, if the player discards two cards, they will receive the 6th and 7th cards on the list during the draw. The location of the discarded cards is irrelevant.

The following description of the application of cryptography presumes the reader has a fundamental understanding of the concept. For the basics, please consult my page on Dice (encrypted version) . For readers who have a more advanced understanding, here’s a detailed outline of how the game selects ten random cards.

1. Initiate a pointer named 'position' and set it to 0.
2. Concatenate the client seed and server seed in the specified order.
3. Create a SHA-512 hash of the combined string from the previous step.
4. Transform the first two characters, starting from the 'position' indicated in the hash from the previous step, converting them from hexadecimal to decimal.
5. Extract the last two digits from the result of the previous step.
6. If the value derived is 51 or less and hasn't been previously selected, it will be included as one of the first ten cards.
7. Increment the \"position\" by 2.
8. Repeat the steps 4 through 7 until ten unique cards are identified.
9. The first five cards will be dealt initially from left to right.
10. The next five cards will queue up to be drawn. For example, if the player draws three cards, they will receive the 6th, 7th, and 8th cards from the queue.
11. To translate the card position from step 6 into an actual playing card, follow this method:
    • A. Divide the figure obtained from step 4 by 13 and take the remainder.
    • B. Use the remainder from step 11A to determine the rank, as follows: 0 corresponds to A, 1 corresponds to 2, 2 to 3, ..., 9 to 10, 10 to J, 11 to Q, and 12 to K.
    • C. Divide the figure from step 4 by 13 and discard the remainder.
    • D. Utilize the result from step 11C to determine the suit, as follows: 0 corresponds to spades, 1 to hearts, 2 to diamonds, and 3 to clubs.

The table below illustrates how numbers are converted into playing cards.

It’s time for an illustrative example, isn’t it? Let’s take a look.

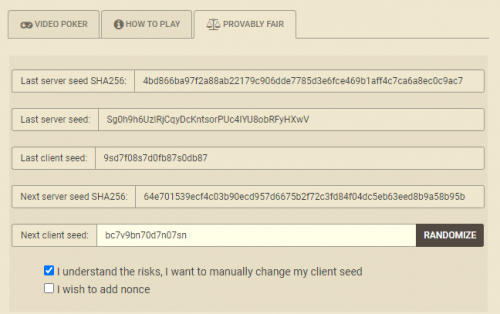
In the 'Probably Fair' interface depicted earlier, my primary goals are to select MY OWN (instead of the default) Client Seed (bc7v9bn70d7n07sn), and to capture the Hash of the upcoming Server Seed (64e701539ecf4c03b90ecd957d6675b2f72c3fd84f04dc5eb63eed8b9a58b95b), which is shown under the 'Next server seed SHA256' row.

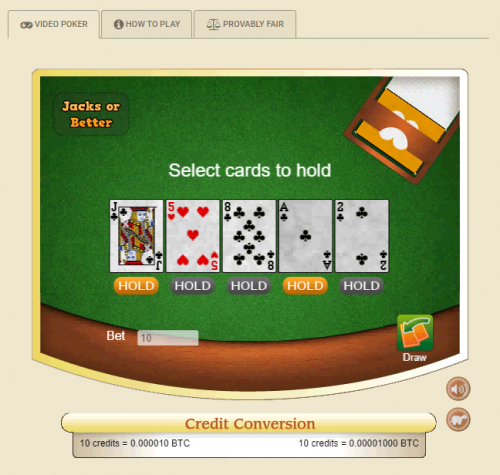
In the image above, I hold a jack and ace of different suits in the first and fourth positions.

In the image above, I manage to form a pair of jacks during the draw.

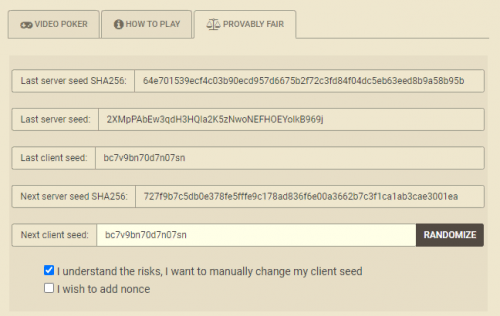
In the preceding screenshot, I returned to the 'Fair Gaming' interface to observe how the casino combines the two seeds to reveal the actual cards dealt in the game.

The displayed screen provides the necessary information to determine what cards should have been dealt. I will walk through it step by step:

1. The instructions are somewhat unclear, but you are expected to join the Server Seed with the Client Seed, in the specified order. This results in 2XMpPAbEw3qdH3HQla2K5zNwoNEFHOEYolkB969jbc7v9bn70d7n07sn.
2. Next, obtain the Hash of the result from the previous step, which produces 3a959bbaffd9b3928b28431c2ee688792c67a45f1933b9e11af3c7784a7bbda5674d2e768ac330a04982b9fa943c4c2cf49c952d9db956b1cd3b38c006c3a2d6. Keep in mind that each character is a numeral from 0 to 9 or a letter from A to F, and the entire string represents a substantial number in hexadecimal notation.
3. Take the initial two characters from the Hash (3a) and convert them from hexadecimal to decimal: 3 multiplied by 16¹+ a*16⁰= 48 + 10 = 58.
4. Derive the last two digits from step 3 (there are only two digits), which translates to 58.
5. If the value from step 4 falls between 0 and 51, it is mapped to a card. Since 58 exceeds 51, we proceed to the next two digits in the Hash.
6. The next two digits from the Hash are 95. This equates to 9 multiplied by 16¹ + 5*16⁰= 144 + 5 = 149 in base 10.
7. The last two digits of 149 are 49, which fits within the 0 to 51 range, enabling its mapping to a card. Specifically, 49 corresponds to the Jacks of Clubs, which will be the first card dealt from the left.
8. Acquire the following two digits from the Hash (9b) and convert them from hexadecimal to decimal: 9 multiplied by 16¹+ b*16⁰= 144 + 11 = 155.
9. Take the last two digits from the last calculation, which results in 55.
10. Since 55 does not fall within the range of 0 to 51, we will skip those two digits in the Hash.
11. Acquire the next two digits in the Hash (ba) and convert them from hexadecimal to decimal: b multiplied by 16¹+ a*16⁰= 11*16 + 10*1 = 176 + 10 = 186.
12. Retrieve the last two digits from this step, which gives us 86.
13. As 86 exceeds the 0 to 51 range, we will bypass those two digits in the Hash.
14. Acquire the next two digits in the Hash (ff) and convert them from hexadecimal to decimal: f multiplied by 16¹+ f*16⁰= 15*16 + 15*1 = 240 + 15 = 255.
15. Take the last two digits from the last calculation, which results in 55.
16. Since 55 does not fall within the range of 0 to 51, we will skip those two digits in the Hash.
17. Now, consider the next two digits in the Hash (d9) and convert them from hexadecimal to decimal: d multiplied by 16¹ + 9*16⁰= 13*16 + 9*1 = 208 + 9 = 217.
18. Retrieve the last two digits of this step, which is 17.
19. Since 17 falls within the range of 0 to 51, it can be mapped to a card. Specifically, 17 corresponds to the 5 of hearts, which will be the second card dealt from the left.
20. Now, retrieve the next two digits in the Hash (b3) and convert them from hexadecimal to decimal: 11 multiplied by 16¹ + 3*16⁰= 13*16 + 9*1 = 176 + 3 = 179.
21. Get the last two digits from the previous step, which equals 79.
22. Since 79 exceeds the range of 0 to 51, we will not consider those two digits in the Hash.
23. Now, take the next two digits in the Hash (92) and convert them from hexadecimal to decimal: 9 multiplied by 16¹ + 2*16⁰= 9*16 + 2*1 = 208 + 9 = 146.
24. Begin by examining the last two digits from the previous calculation, which are 46.
25. Since 46 falls within the range of 0 to 51, we can assign it to a corresponding card. Specifically, 46 corresponds to the 8 of clubs. This card will be the third one dealt from the left.
26. Now move on to the next pair of digits in the Hash (8b) and convert them from hexadecimal to their decimal equivalent: 8 times 16.¹ + 11*16⁰= 9*16 + 2*1 = 128 + 11 = 139.
27. Next, take the last two digits from the previous step, which are 39.
28. The value 39 is also within the range of 0 to 51, so we will map it to a card. It corresponds to the ace of clubs, which will be the fourth card dealt from the left.
29. Proceed to the subsequent two digits in the Hash (28) and change them from hexadecimal to decimal: 2 times 16.¹ + 8*16⁰= 2*16 + 8*1 = 32 + 8 = 40.
30. The number 40 is within the range of 0 to 51, allowing us to map it to a card—specifically, it represents the 2 of clubs. This will be the final card dealt, positioned on the right side.
31. After discarding three cards, it becomes necessary to locate the next three distinct cards in the Hash to substitute them.
32. Take the following two digits in the Hash (43) and transform them from hexadecimal into decimal: 4 times 16.¹ + 3*16⁰= 4*16 + 3*1 = 67.
33. Next, focus on the two digits in the Hash (1c) and convert them from hexadecimal to decimal: 1 times 16.¹+ c*16⁰= 1*16 + 12*1 = 38.
34. The value 38, which fits into the 0 to 51 range and hasn't been encountered before, maps to a card—the 3 of diamonds. This will be the first card drawn.
35. Now, consider the next two digits in the Hash (2e) and convert them from hexadecimal to decimal: 2 times 16.¹+ e*16⁰= 2*16 + 14*1 = 32 + 14 = 46.
36. Since 46 has already been processed, we will skip those two positions in the Hash.
37. Now move on to the next pair of digits in the Hash (e6) and convert them from hexadecimal to decimal: e times 16.¹ + 6*16⁰= 14*16 + 6*1 = 230.
38. Take the last two digits from the previous step, which are 30.
39. The value 30 is within the range of 0 to 51 and hasn’t been noted yet, so we can assign it to a card. Specifically, 30 maps to the 5 of diamonds, which will be the second card to replace.
40. Next, look at the following two digits in the Hash (88) and switch them from hexadecimal to decimal: 8 times 16.¹ + 8*16⁰= 136.
41. Take the last two digits from the previous step, which are 36.
42. The value 36 is within the range of 0 to 51 and has not been encountered yet, allowing us to associate it with a card. Specifically, 36 corresponds to the jack of diamonds. This will represent the third replacement card.
43. There is no need to search for additional cards. The hand is prepared for scoring, and the payout to the player is set.

In summary, the table below outlines pairs of characters from the Hash, their decimal conversions, and the corresponding card mappings, if applicable.

Key:
o/r denotes a decimal conversion value that falls outside the acceptable range for a card.
r/p/c = Repeat of previous card

If this seems like an excessive process to ensure fairness, I'm pleased to inform you that I've created a script that automates this for you. It's conveniently saved at the PHP Sandbox . This tool is incredibly helpful! To utilize it, simply enter the Server (casino) Seed on line 4, input your Client (personal) Seed on line 5, and then click Execute Code. The result box below will indicate the cards you were predetermined to receive.

Should anything occur with the code, you can view the script by clicking the button below.

This section discusses a video poker gameplay technique that utilizes encryption to guarantee predetermined card outcomes. If you're new to the fundamental rules of video poker, please refer to my primary page. video poker page.

Currently, my focus is on Cypto.Games. They offer three different variations of video poker, which are detailed as follows:

• Jacks or better
• Tens or better
• Bonus poker

A player is required to place a bet of 10 credits, though they have the flexibility to determine the equivalent value in Cryptocurrency. Personally, I believe that the step involving ten credits complicates the process unnecessarily.

After that, click Execute Code. The results box below will display both the cards you were assigned and a confirmation that the Server Seed hashes to what was provided prior to the bet.

I also present a copy of the code below.

Video Poker Fair Gaming Code

// This section converts the video poker game for Crypto.Games
$server_seed = \"2XMpPAbEw3qdH3HQla2K5zNwoNEFHOEYolkB969j\";
$client_seed = \"bc7v9bn70d7n07sn\";
$next_hash = \"64e701539ecf4c03b90ecd957d6675b2f72c3fd84f04dc5eb63eed8b9a58b95b\";
$rank_array=array(\"A\",2,3,4,5,6,7,8,9,10,\"J\",\"Q\",\"K\");
$suit_array=array(\"spades\",\"hearts\",\"diamonds\",\"clubs\");
$cards_found=0;
$position=0;
$combined_seed = $server_seed.$client_seed;
echo \"Combined seed = $combined_seed\
\";
$combined_hash = hash(\"sha512\", $combined_seed);
echo \"Hash of combined seed = $combined_hash\
\";
do
{
$first_two=substr($combined_hash,$position,2);
$hex_to_dec=hexdec($first_two)0;
if ($hex_to_dec <=51)
{
$repeat=0;
if ($cards_found>0)
{
for ($i=0; $i<$cards_found; $i++)
{
if ( $hex_to_dec == $card_array[$i])
{ $repeat=1; }
}
}
if ($repeat==0)
{
$card_array[$cards_found] = $hex_to_dec;
$game_position=1+($cards_found%5);
$cards_found++;
$rank=$hex_to_dec;
$suit=intdiv($hex_to_dec,13)%4;
if ($cards_found<=5)
{   echo \"Deal card $game_position =\\t$rank_array[$rank] of $suit_array[$suit]\
\"; }
else
{   echo \"Draw card $game_position =\\t$rank_array[$rank] of $suit_array[$suit]\
\"; }
}
}
$position+=2;
if ($position==128)
{
echo \"Error -- No more space in hash.\
\";
$cards_found=10;
}
}
while ($cards_found<10);
$server_seed_hash = hash(\"sha256\", $server_seed);
if ($server_seed_hash==$next_hash)
{ echo \"Server Seed match.
\"; }
else
{
echo \"SERVER SEED MISMATCH!
\";
echo \"Server seed      =\\t$server_seed\
\";
echo \"Server seed Hash =\\t$server_seed_hash\
\";
echo \"Alleged next Hash=\\t$next_hash\
\";
}
// Procedure
// 1.  Step the \"position\" to 0.
// 2.  Combine the server and client seeds along with the server seed in that order.
// 3.  Create a SHA-512 hash from the string generated in step 2.
// 4.  Convert the first two characters, beginning at the specified \"position\" of the hash from step 3, from hexadecimal to decimal.
// 5.  Extract the final two digits from step 4.
// 6.  If the result from step 5 is 51 or less, and it hasn't been previously identified, then that will be considered one of the first ten cards.
// 7.  Increment the \"position\" by 2.
// 8.  Keep repeating steps 4 through 7 until ten distinct cards have been located.
// 9.  The first five cards identified will be dealt in the order they were found, starting from the left.
// 10. The subsequent five cards will be held in a queue for later. For instance, if the player draws three cards, they will receive the 6th, 7th, and 8th cards from the queue.
// 11. To determine the position of a card from step 6 and convert it into an actual card, follow these steps:
//     A.  Divide the result from step 4 by 13 and retain the remainder.
//     B.  Map the outcome from step 11A to assign the rank using the following: 0 corresponds to A, 1 to 2, 2 to 3, ..., 9 to 10, 10 to J, 11 to Q, and 12 to K.
//     C.  Divide the result from step 4 by 13 and discard the remainder.
//     D.  Map the result from step 11C to determine the suit: 0 for spades, 1 for hearts, 2 for diamonds, and 3 for clubs.
?>

Written by: Michael Shackleford