4 beats 5
1 beats 1
Sat Jun 14th 02am
Indiana Pacers
Oklahoma City Thunder
A common inquiry during March is, \"What are the odds of accurately completing a March Madness bracket?\" A prevalent statistic circulated in media sources is 1 in 9,223,372,036,854,780,000. This figure is derived from the idea of random guesses, which is hardly how real participants approach it, and it certainly makes me uneasy. In this section, I'll outline a straightforward strategy that requires no basketball knowledge and provide an estimate of your chances of winning using this approach.
Line
Here are the tournament's guidelines. If you're already familiar with them, feel free to skip this section.
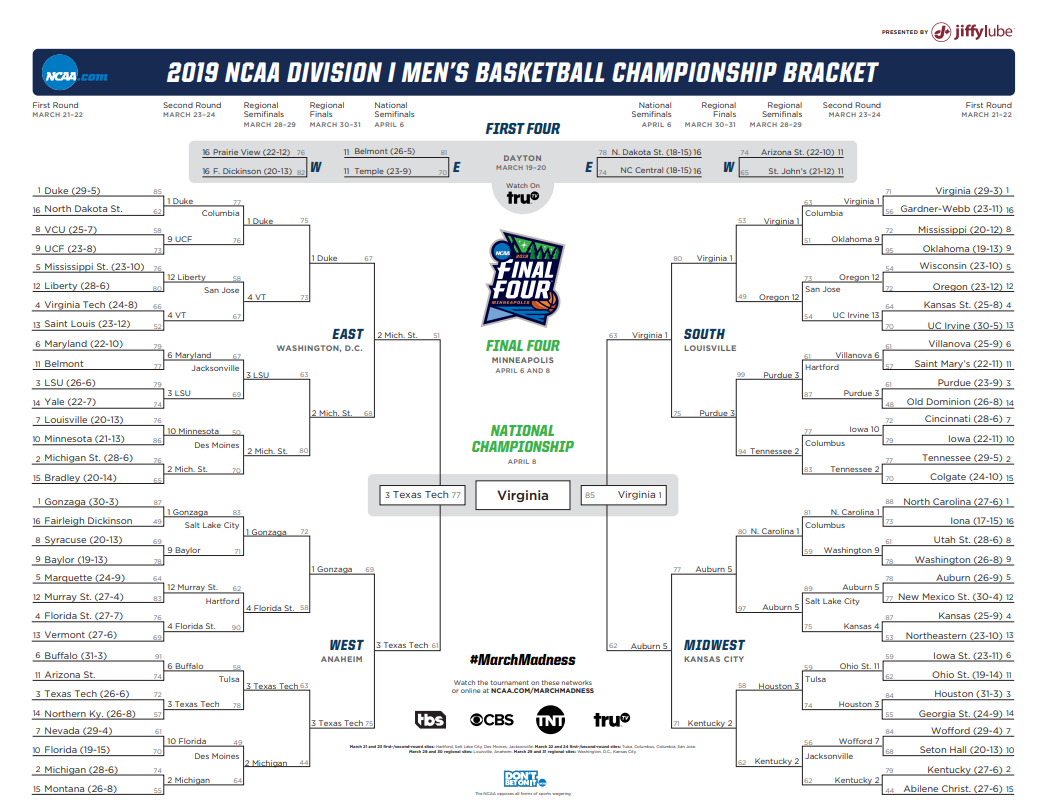
Generally speaking, the tournament operates on a single elimination format, initiating with 64 teams. To address my detail-oriented audience, it’s worth mentioning that the actual number is 68. This includes eight teams that compete in four preliminary games. The four victors from those matchups, combined with 60 other teams, create a total of 64 teams, marking the start of bracket selection.
These 64 teams are categorized into four distinct regions: North, South, West, and East, each comprising 16 teams. Within each region, every team is assigned a seed ranging from 1 to 16, intended to represent their performance level, although this isn’t a flawless assessment. The process unfolds as follows:
- The four top-seeded teams will face off against the four lowest-seeded teams.
- The four eighth-seeded teams will compete against the four ninth-seeded teams.
- The four fifth-seeded teams will battle it out with the four twelfth-seeded teams.
- The four fourth-seeded teams will match against the four thirteenth-seeded teams.
- The four sixth-seeded teams will play against the four eleventh-seeded teams.
- The four third-seeded teams will square off against the four fourteenth-seeded teams.
- The four second-seeded teams will contend with the four fifteenth-seeded teams.
- The four seventh-seeded teams will face the four tenth-seeded teams.
- Following the matches from steps 1 through 8, the field of 64 will be reduced to 32 teams.
- The winners of the matchups in rule 1 will then compete against those in rule 2.
- The victors of rule 3 will take on the winners of rule 4.
- The champions of rule 5 will match up with those from rule 6.
- The teams that win in rule 7 will go against the winners in rule 8.
- At the conclusion of the matches in steps 10 to 13, the total will be narrowed down to 16 teams.
- The champions from rule 10 will compete against the victors from rule 11.
- The winners from rule 12 will match up with those from rule 13.
- After the games in steps 15 and 16, only eight teams will remain.
- The winners of rule 15 will face off against the winners of rule 16.
- After the matches from step 18, the remaining eight teams will be reduced to just 4, determining a champion in each regional division.
- The champion from the region that boasts the top overall seed, as designated by the NCAA basketball committee, will play the winner from the region with the fourth overall seed, allowing one team to advance.
- The victors from the two regions not covered in rule 20 will square off, with the winner progressing further.
- The winners of steps 20 and 21 will collide, with one team ultimately claiming the tournament title.
Once the count reaches 64 teams, a total of 63 games will be held throughout the tournament, broken down as 32 + 16 + 8 + 4 + 2 + 1.
William Hill
Always opt for the team that has the superior seed, meaning a lower number. For instance, in the matchups involving a number 1 seed against a number 16 seed, one should select the number 1 seed. In all history, a number 1 seed has faced a 16 seed 136 times, with the 1 seed triumphing 135 times. It was only in 2018 that a number 1 seed was defeated by a 16 seed when UMBC triumphed over the University of Virginia, which is known for its strong chess team.
If all four divisions are won by number one seeds, you can randomly select the outcomes for the remaining three games.
William Hill Casino
The following table illustrates the various matchups that have occurred with unbalanced seeds at least once. It does not cover instances where teams of equal seed faced each other. The last column indicates the likelihood of the higher-ranked team achieving victory.
Claim
| Matchbook | Matchbook Casino | Claim | Spread | Matchbook |
|---|---|---|---|---|
| 1 | 2 | 67 | 36 | 0.537313 |
| 1 | 3 | 36 | 22 | 0.611111 |
| 1 | 4 | 64 | 47 | 0.734375 |
| 1 | 5 | 48 | 40 | 0.833333 |
| 1 | 6 | 13 | 10 | 0.769231 |
| 1 | 7 | 7 | 6 | 0.857143 |
| 1 | 8 | 75 | 60 | 0.800000 |
| 1 | 9 | 71 | 65 | 0.915493 |
| 1 | 10 | 6 | 5 | 0.833333 |
| 1 | 11 | 8 | 4 | 0.500000 |
| 1 | 12 | 20 | 20 | 1.000000 |
| 1 | 13 | 4 | 4 | 1.000000 |
| 1 | 16 | 144 | 143 | 0.993056 |
| 2 | 3 | 56 | 34 | 0.607143 |
| 2 | 4 | 7 | 3 | 0.428571 |
| 2 | 5 | 5 | 0 | 0.000000 |
| 2 | 6 | 30 | 23 | 0.766667 |
| 2 | 7 | 82 | 57 | 0.695122 |
| 2 | 8 | 7 | 2 | 0.285714 |
| 2 | 9 | 1 | 0 | 0.000000 |
| 2 | 10 | 52 | 34 | 0.653846 |
| 2 | 11 | 18 | 15 | 0.833333 |
| 2 | 12 | 2 | 2 | 1.000000 |
| 2 | 15 | 144 | 134 | 0.930556 |
| 3 | 4 | 7 | 4 | 0.571429 |
| 3 | 5 | 4 | 2 | 0.500000 |
| 3 | 6 | 75 | 45 | 0.600000 |
| 3 | 7 | 15 | 9 | 0.600000 |
| 3 | 8 | 2 | 2 | 1.000000 |
| 3 | 9 | 2 | 2 | 1.000000 |
| 3 | 10 | 12 | 8 | 0.666667 |
| 3 | 11 | 49 | 32 | 0.653061 |
| 3 | 14 | 144 | 122 | 0.847222 |
| 3 | 15 | 2 | 2 | 1.000000 |
| 4 | 5 | 75 | 42 | 0.560000 |
| 4 | 6 | 4 | 2 | 0.500000 |
| 4 | 7 | 5 | 2 | 0.400000 |
| 4 | 8 | 9 | 4 | 0.444444 |
| 4 | 9 | 3 | 2 | 0.666667 |
| 4 | 10 | 2 | 2 | 1.000000 |
| 4 | 12 | 39 | 26 | 0.666667 |
| 4 | 13 | 144 | 113 | 0.784722 |
| 5 | 6 | 1 | 1 | 1.000000 |
| 5 | 8 | 3 | 1 | 0.333333 |
| 5 | 9 | 3 | 1 | 0.333333 |
| 5 | 10 | 1 | 1 | 1.000000 |
| 5 | 12 | 144 | 93 | 0.645833 |
| 5 | 13 | 19 | 16 | 0.842105 |
| 6 | 7 | 9 | 6 | 0.666667 |
| 6 | 8 | 1 | 0 | 0.000000 |
| 6 | 10 | 7 | 4 | 0.571429 |
| 6 | 11 | 144 | 90 | 0.625000 |
| 6 | 14 | 15 | 13 | 0.866667 |
| 7 | 8 | 2 | 1 | 0.500000 |
| 7 | 10 | 144 | 87 | 0.604167 |
| 7 | 11 | 3 | 0 | 0.000000 |
| 7 | 14 | 1 | 1 | 1.000000 |
| 7 | 15 | 5 | 3 | 0.600000 |
| 8 | 9 | 144 | 74 | 0.513889 |
| 8 | 11 | 1 | 1 | 1.000000 |
| 8 | 12 | 2 | 0 | 0.000000 |
| 8 | 13 | 1 | 1 | 1.000000 |
| 8 | 16 | 1 | 0 | 0.000000 |
| 9 | 11 | 1 | 0 | 0.000000 |
| 9 | 13 | 1 | 1 | 1.000000 |
| 10 | 11 | 3 | 1 | 0.333333 |
| 10 | 14 | 1 | 1 | 1.000000 |
| 10 | 15 | 5 | 5 | 1.000000 |
| 11 | 14 | 7 | 6 | 0.857143 |
| 12 | 13 | 12 | 9 | 0.750000 |
Matchbook Casino
In the past, I used to evaluate the odds of completing a flawless bracket by examining historical data on seed matchups. For instance, looking at a 4 seed versus a 5 seed scenario. With data spanning 36 years, from 1985 to 2021, this matchup occurred 75 times with the 4 seed winning 42 of those encounters, yielding a probability of 56%. While this method has its merits, it suffers from having a limited set of data. A more effective approach to gauging the probability of the higher seeded team winning any match, based on their seed numbers, is to analyze all 2,268 tournament games played over those 36 years. This method helps smooth out the fluctuations in the statistics, leading to a more accurate estimate. A deeper dive into this can be found on my dedicated page. Claim .
The subsequent table reveals the odds of the higher seed emerging victorious in any matchup that's required for winning when consistently choosing the higher seeded team. In instances where a 1 seed faces another 1 seed, I consider it a 50% chance of winning. The older assessment refers to the actual matchup probabilities based on historical data. In contrast, the newer method relies on my technique to give a clearer view of the relative strength of each seed.
888sport
| 888 Casino | Sign Up Bonus - Sports | €30 | Players rated 888 Casino 3.6 out of 5 Stars Claim |
(-6.5) ⇗0.15 |
|---|---|---|---|---|
| 1 | Total | 4 | 0.993056 | 0.993049 |
| 1 | 1xBet | 4 | 0.930556 | 0.933458 |
| 1 | 1XBET Casino | 4 | 0.847222 | 0.887485 |
| 1 | Sign Up Bonus | 4 | 0.784722 | 0.832170 |
| 1 | 100% up to | 4 | 0.645833 | 0.768372 |
| 1 | €300 | 4 | 0.625000 | 0.697340 |
| 1 | +30 spins | 4 | 0.604167 | 0.620749 |
| 1 | Claim | 4 | 0.513889 | 0.540650 |
| 2 | Matchbook | 4 | 0.800000 | 0.792047 |
| 2 | Matchbook Casino | 4 | 0.560000 | 0.540873 |
| 2 | Claim | 4 | 0.600000 | 0.622246 |
| 2 | ⇗0.04 | 4 | 0.695122 | 0.702952 |
| 3 | Featured Insight | 4 | 0.734375 | 0.668944 |
| 3 | wnba_us_basketball.png | 4 | 0.607143 | 0.551538 |
| 4 | Basketball | 4 | 0.537313 | 0.578959 |
| 5 | WNBA | 2 | 0.500000 | 0.500000 |
| 6 | This Week | 1 | 0.500000 | 0.500000 |
Before we proceed, let's clarify the notation as pr(x) = probability of the event x occurring. As an illustration, pr(rolling a total of 7 with two dice) equals 1/6.
Keep in mind that with four divisions in the tournament, a player must succeed in winning any single matchup throughout the first four rounds.
The chance of winning all 32 games in the initial round and moving on to the second round is calculated as: [pr(1 seed defeats 16 seed)*pr(2 seed defeats 15 seed)*pr(3 seed defeats 14 seed)*pr(4 seed defeats 13 seed)*pr(5 seed defeats 12 seed)*pr(6 seed defeats 11 seed)*pr(7 seed defeats 10 seed)*pr(8 seed defeats 9 seed)]^4.
Using the newer methodology, the probability of making it to round 2 stands at 1 in 4,354.
In the second round, a player must win a total of 16 games. Assuming they make it out of round 1, the chance of surviving round 2 will be [pr(1 seed defeats 8 seed)*pr(2 seed defeats 7 seed)*pr(3 seed defeats 6 seed)*pr(4 seed defeats 5 seed)]^4. With this new calculation, the odds of advancing to this round are 1 in 811. Consequently, the combined chance of surviving both rounds 1 and 2 is about 1 in 3,531,138.
Moving into round 3, there are 8 games to conquer. Provided survival through rounds 1 and 2, the probability of progressing in round 3 is calculated as [pr(1 seed defeats 4 seed)*pr(2 seed defeats 3 seed)]^4. Under this updated strategy, the odds are 1 in 54. Thus, from the outset, the total survival probability is around 1 in 190 million.
As we enter round 4, there will be 4 games in total. Since these will all be battles between 1 seed and 1 seed, let’s assume each game has a 50/50 chance of winning. The probability of winning all four games is calculated as (1/2)^4 = 1 in 16. Therefore, the chance of making it to this stage from the start is near 1 in 1.7 billion.
In round 5, players will contend in 2 games—all between number one seeds. Again, assuming a 50% chance of winning per game, the odds of taking both games is (1/2)^2 = 1 in 4. This translates to a survival probability from the start of approximately 1 in 6.8 billion.
One final game remains, the championship match. If players have progressed this far, it will again be between two one seeds. Assuming a 50% win rate, this further raises the likelihood of completing a perfect bracket through to the championship match to about 1 in 13.6 billion.
It's worth noting that utilizing the traditional method estimates the odds of achieving a flawless bracket at 1 in 56.7 billion.
Sat Jun 14th 01am
Warren Buffett has pledged $1 million annually, for life, to any employee who can submit a perfect bracket. Given that Warren has around 377,000 employees, if each one applied the aforementioned strategy and lived for another 60 years, the anticipated value for each employee would amount to just 0.4 cents, resulting in a total expected payout to Mr. Buffet of approximately $1,667. Atlanta Dream If you want to ensure your perfect bracket remains uniquely yours without sharing the spotlight, I recommend selecting one or two 9 seeds to defeat an 8 seed. With a 47.8% chance of success for the nine seed over the eight seed, this small sacrifice could enhance your odds of securing the glory for yourself.
Players have evaluated William Hill Casino with a score of 3.7 out of 5 stars.
Chicago Sky
Line Nordic Bet
Nordic Bet
NordicBet Casino
2.12
(5)
2.02
(224.5) Dallas Wings
Nordic Bet NordicBet Casino
Be Gamble Aware logo
Gordon Moody logo
Copyright & 1998-2025. All rights reserved.
Privacy Policy
You have successfully logged in!One question that frequently arises in March is, \"What are the odds of completing a March Madness bracket without any mistakes?\" A commonly cited figure you might hear in the media is 1 in 9,223,372,036,854,780,000. This number stems from a random guessing perspective, which is unrealistic and tends to send chills down my spine. Here, I will outline a simple strategy you can adopt even without any basketball knowledge and provide an estimation of your chances for success using this approach. .