On this page
Poker Dice
Introduction
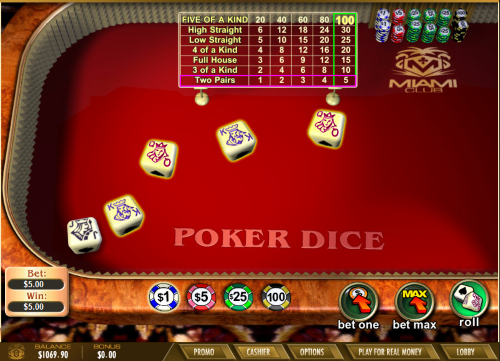
Poker Dice is a chance-based game offered by online casinos that utilizes specific Wager Gaming Technology and 1x2 Gaming software. Players roll five specially designed poker dice, aiming to create a winning poker combination.
Rules
- The player makes a bet.
- This game incorporates five poker dice, each displaying a 9, 10, jack, queen, king, and ace on its faces.
- Winnings are determined based on the poker ranking of the five rolled dice, as outlined in a designated pay table. All payouts are structured on a 'for one' basis.
Wager Gaming Pay Table
| Hand | Pays |
|---|---|
| Five of a kind | 100 |
| High straight | 6 |
| Low straight | 5 |
| Four of a kind | 4 |
| Full house | 3 |
| Three of a kind | 2 |
| Two pair | 1 |
| Loser | 0 |
1x2 Gaming Pay Table
| Hand | Pays |
|---|---|
| Golden royal | 50 |
| Golden straight | 35 |
| Five of a kind | 20 |
| High straight | 6 |
| Low straight | 5 |
| Four of a kind | 4 |
| Full house | 3 |
| Three of a kind | 2 |
| Two pair | 1 |
| Pair of aces | 0.5 |
A Golden Royal consists of a seamless succession leading to the ace. The arrangement of the dice must follow a defined order. A Golden Straight, meanwhile, extends to the king in a sequential manner. The correctly organized dice are highlighted in a golden shade.
Wager Gaming Analysis
The table below indicates various combinations, their probabilities, and the expected returns from each result. The bottom right corner reflects a return rate of 97.99%.
Return Table
| Hand | Pays | Permutations | Probability | Return | |
|---|---|---|---|---|---|
| Five of a kind | 100 | 6 | 0.000772 | 0.077160 | |
| High straight | 6 | 120 | 0.015432 | 0.092593 | |
| Low straight | 5 | 120 | 0.015432 | 0.077160 | |
| Four of a kind | 4 | 150 | 0.019290 | 0.077160 | |
| Full house | 3 | 300 | 0.038580 | 0.115741 | |
| Three of a kind | 2 | 1,200 | 0.154321 | 0.308642 | |
| Two pair | 1 | 1,800 | 0.231481 | 0.231481 | |
| Loser | 0 | 4,080 | 0.524691 | 0.000000 | |
| Total | 7,776 | 1.000000 | 0.979938 |
1x2 Gaming Analysis
Another table presents the combinations, chances, and possible returns for each outcome, with the bottom right corner indicating a return rate of 96.63%.
Return Table
| Hand | Pays | Permutations | Probability | Return |
|---|---|---|---|---|
| Golden royal | 50 | 1 | 0.000129 | 0.006430 |
| Golden straight | 35 | 1 | 0.000129 | 0.004501 |
| Five of a kind | 20 | 6 | 0.000772 | 0.015432 |
| High straight | 6 | 119 | 0.015303 | 0.091821 |
| Low straight | 5 | 119 | 0.015303 | 0.076517 |
| Four of a kind | 4 | 150 | 0.019290 | 0.077160 |
| Full house | 3 | 300 | 0.038580 | 0.115741 |
| Three of a kind | 2 | 1,200 | 0.154321 | 0.308642 |
| Two pair | 1 | 1,800 | 0.231481 | 0.231481 |
| Pair of aces | 0.5 | 600 | 0.077160 | 0.038580 |
| All other | 0 | 3,480 | 0.447531 | 0.000000 |
| Total | 7,776 | 1.000000 | 0.966307 |
Math Lesson
I elaborate on the count of permutations for each hand on my page, Dazzling Dice , excluding two pairs, as they don't yield any payouts in this game.
In a two pair, there are combin (6,2) equals 15 distinct ways to select two ranks from five for the two pairs. Subsequently, there are four remaining options to pick the rank of the single die. The number of ways to position the first pair is given by combin(5,2)=10, while combin(3,2)=3 provides the positioning for the second pair. Therefore, the total permutations for achieving two pairs is 15×4×10×3 = 1,800.
External Links
- Poker Dice on the F1x2 platform — Details pertaining to the Poker Dice version by 1x2 Gaming. Without this information, I would have remained unaware of the concepts of Golden Royal and Golden Straight.
- What is a Golden Royal — A reflection on my challenges regarding the clarification of what constitutes a Golden Royal.
