On this page
Pineapple
On this page
Introduction
This section aims to explain how to make the initial decision regarding your hand in the poker variant known as Pineapple. If you're unfamiliar, Pineapple is similar to Texas Hold 'Em, but players receive three hole cards and must discard one after a preliminary betting round, prior to the flop. It’s important not to confuse this with Crazy Pineapple, where the card removal happens right before the Turn, or Lazy Pineapple, where players retain all three cards throughout the gameplay.
This section's primary focus is on the choice of which card to discard, along with an examination of the strength of each starting hand. On this page, you will discover statistics regarding expected value, which indicates how much a player can anticipate returning based on a single unit ante. For instance, an expected return of 1.000 implies that a player is breaking even.
A term you'll frequently encounter here is 'penalty', a concept borrowed from video poker. This refers to the act of discarding a card that might have been beneficial. Specifically, a rank penalty occurs when you toss away a card after being dealt a three of a kind. This can be quite disheartening in Pineapple, as losing one of these cards not only diminishes your hand's value but also reduces the total number of cards available to potentially improve your pair. Suit penalties are even more common; discarding a suited card that matches one you are keeping decreases your chances of achieving a flush. Ideally, you want to avoid any kind of penalty altogether.
 Recommended Online Poker Rooms in Poland
Recommended Online Poker Rooms in Poland
View All
Assumptions
This section assumes a scenario where six players engage in a game where nobody ever folds or raises. Each participant contributes one unit as an ante, and the player with the best hand at the conclusion of the game wins.
Three of a Kind
The strategy when you are dealt three of a kind is straightforward—simply hold onto any two of those cards.
The table below illustrates the expected return of retaining any two cards when you're dealt a three of a kind.
Dealt Three of Kind
| Rank | Expected Return |
|---|---|
| A | 2.425 |
| K | 1.925 |
| Q | 1.563 |
| J | 1.297 |
| 10 | 1.084 |
| 9 | 0.899 |
| 8 | 0.777 |
| 7 | 0.687 |
| 6 | 0.624 |
| 5 | 0.571 |
| 4 | 0.521 |
| 3 | 0.483 |
| 2 | 0.448 |
Pair without Suit Penalty
When you have a pair, the strategy is quite simple—keep the pair.
The subsequent table displays the expected returns for the two effective strategies when dealt a pair and an unrelated card, provided that the single card is not suited to any of the cards in the pair. You can either hold the pair or the singleton alongside either of the two in the pair. The data clearly indicates that maintaining the pair is consistently the option with the highest expected value.
Dealt Three of Kind
| Rank | Singleton | Pair | Two Singletons |
|---|---|---|---|
| A | K | 2.708 | 1.289 |
| A | Q | 2.719 | 1.159 |
| A | J | 2.729 | 1.059 |
| A | 10 | 2.740 | 0.985 |
| A | 9 | 2.739 | 0.827 |
| A | 8 | 2.734 | 0.785 |
| A | 7 | 2.736 | 0.753 |
| A | 6 | 2.737 | 0.722 |
| A | 5 | 2.734 | 0.777 |
| A | 4 | 2.719 | 0.753 |
| A | 3 | 2.701 | 0.728 |
| A | 2 | 2.674 | 0.694 |
| K | A | 2.392 | 1.276 |
| K | Q | 2.224 | 1.082 |
| K | J | 2.237 | 0.999 |
| K | 10 | 2.245 | 0.936 |
| K | 9 | 2.246 | 0.784 |
| K | 8 | 2.243 | 0.683 |
| K | 7 | 2.245 | 0.661 |
| K | 6 | 2.247 | 0.641 |
| K | 5 | 2.245 | 0.622 |
| K | 4 | 2.234 | 0.603 |
| K | 3 | 2.219 | 0.582 |
| K | 2 | 2.201 | 0.562 |
| K | Q | 1.999 | 1.147 |
| A | Q | 1.994 | 1.080 |
| K | Q | 1.865 | 0.975 |
| J | 10 | 1.880 | 0.920 |
| Q | 9 | 1.876 | 0.773 |
| Q | 8 | 1.877 | 0.676 |
| Return | 7 | 1.879 | 0.592 |
| A | 6 | 1.881 | 0.580 |
| K | 5 | 1.880 | 0.564 |
| Q | 4 | 1.873 | 0.543 |
| J | 3 | 1.859 | 0.525 |
| Pair without Suit Penalty | 2 | 1.847 | 0.509 |
| Dealt Three of Kind | Rank | 1.702 | 1.052 |
| Singleton | Pair | 1.696 | 0.998 |
| Two | Singletons | 1.696 | 0.971 |
| A | 10 | 1.601 | 0.931 |
| K | 9 | 1.600 | 0.792 |
| A | 8 | 1.599 | 0.696 |
| Q | 7 | 1.601 | 0.610 |
| A | 6 | 1.603 | 0.537 |
| J | 5 | 1.606 | 0.523 |
| A | 4 | 1.597 | 0.506 |
| A | 3 | 1.591 | 0.488 |
| A | 2 | 1.582 | 0.474 |
| 10 | A | 1.466 | 0.980 |
| 10 | A | 1.465 | 0.934 |
| 10 | A | 1.464 | 0.918 |
| 10 | A | 1.465 | 0.926 |
| 10 | 9 | 1.388 | 0.823 |
| 10 | 8 | 1.388 | 0.734 |
| 10 | 7 | 1.388 | 0.650 |
| 10 | 6 | 1.394 | 0.569 |
| 10 | 5 | 1.394 | 0.497 |
| 10 | 4 | 1.388 | 0.481 |
| 10 | 3 | 1.383 | 0.465 |
| 10 | 2 | 1.377 | 0.453 |
| 9 | A | 1.284 | 0.815 |
| 9 | A | 1.288 | 0.767 |
| 9 | K | 1.286 | 0.755 |
| 9 | A | 1.287 | 0.769 |
| 9 | 10 | 1.288 | 0.803 |
| 9 | 8 | 1.223 | 0.720 |
| 9 | 7 | 1.224 | 0.663 |
| 9 | 6 | 1.226 | 0.591 |
| 9 | 5 | 1.226 | 0.513 |
| 9 | 4 | 1.225 | 0.438 |
| 9 | 3 | 1.221 | 0.426 |
| 9 | 2 | 1.216 | 0.414 |
| 8 | K | 1.159 | 0.774 |
| 8 | Q | 1.159 | 0.669 |
| 8 | K | 1.160 | 0.655 |
| 8 | J | 1.163 | 0.672 |
| 8 | 10 | 1.162 | 0.708 |
| 8 | 9 | 1.159 | 0.708 |
| 8 | 7 | 1.110 | 0.688 |
| 8 | 6 | 1.110 | 0.635 |
| 8 | 5 | 1.112 | 0.560 |
| 8 | 4 | 1.109 | 0.479 |
| 8 | 3 | 1.108 | 0.407 |
| 8 | 2 | 1.103 | 0.398 |
| 7 | K | 1.059 | 0.739 |
| 7 | K | 1.063 | 0.649 |
| 7 | K | 1.066 | 0.577 |
| 7 | K | 1.068 | 0.584 |
| 7 | 10 | 1.069 | 0.620 |
| 7 | 9 | 1.062 | 0.643 |
| 7 | 8 | 1.065 | 0.673 |
| 7 | 6 | 1.021 | 0.661 |
| 7 | 5 | 1.027 | 0.609 |
| 7 | 4 | 1.024 | 0.532 |
| 7 | 3 | 1.024 | 0.451 |
| 7 | 2 | 1.022 | 0.383 |
| 6 | K | 0.989 | 0.713 |
| 6 | K | 0.994 | 0.629 |
| 6 | K | 0.994 | 0.564 |
| 6 | K | 1.000 | 0.515 |
| 6 | 10 | 1.000 | 0.541 |
| 6 | 9 | 0.997 | 0.568 |
| 6 | 8 | 0.996 | 0.617 |
| 6 | 7 | 0.995 | 0.650 |
| 6 | 5 | 0.962 | 0.643 |
| 6 | 4 | 0.961 | 0.584 |
| 6 | 3 | 0.959 | 0.508 |
| 6 | 2 | 0.960 | 0.429 |
| 5 | K | 0.931 | 0.775 |
| 5 | K | 0.935 | 0.613 |
| 5 | Q | 0.937 | 0.552 |
| 5 | A | 0.939 | 0.507 |
| 5 | 10 | 0.943 | 0.476 |
| 5 | 9 | 0.940 | 0.494 |
| 5 | 8 | 0.940 | 0.543 |
| 5 | 7 | 0.940 | 0.597 |
| 5 | 6 | 0.937 | 0.635 |
| 5 | 4 | 0.911 | 0.633 |
| 5 | 3 | 0.906 | 0.571 |
| 5 | 2 | 0.909 | 0.500 |
| 4 | Q | 0.882 | 0.749 |
| 4 | K | 0.887 | 0.590 |
| 4 | Q | 0.891 | 0.530 |
| 4 | J | 0.891 | 0.487 |
| 4 | 10 | 0.893 | 0.458 |
| 4 | 9 | 0.894 | 0.420 |
| 4 | 8 | 0.891 | 0.460 |
| 4 | 7 | 0.895 | 0.514 |
| 4 | 6 | 0.891 | 0.570 |
| 4 | 5 | 0.891 | 0.623 |
| 4 | 3 | 0.866 | 0.534 |
| 4 | 2 | 0.864 | 0.478 |
| 3 | Q | 0.843 | 0.723 |
| 3 | Q | 0.848 | 0.568 |
| 3 | Return | 0.850 | 0.509 |
| 3 | A | 0.852 | 0.467 |
| 3 | 10 | 0.853 | 0.440 |
| 3 | 9 | 0.851 | 0.404 |
| 3 | 8 | 0.854 | 0.386 |
| 3 | 7 | 0.853 | 0.429 |
| 3 | 6 | 0.853 | 0.488 |
| 3 | 5 | 0.851 | 0.556 |
| 3 | 4 | 0.851 | 0.525 |
| 3 | 2 | 0.829 | 0.440 |
| 2 | K | 0.816 | 0.683 |
| 2 | Q | 0.818 | 0.544 |
| 2 | J | 0.823 | 0.489 |
| 2 | Pair without Suit Penalty | 0.823 | 0.445 |
| 2 | 10 | 0.826 | 0.421 |
| 2 | 9 | 0.824 | 0.386 |
| 2 | 8 | 0.823 | 0.374 |
| 2 | 7 | 0.826 | 0.360 |
| 2 | 6 | 0.824 | 0.403 |
| 2 | 5 | 0.824 | 0.478 |
| 2 | 4 | 0.823 | 0.459 |
| 2 | 3 | 0.821 | 0.431 |
Dealt Three of Kind
When you have a pair, the strategy is quite simple—keep the pair.
The following table presents the expected returns for all three potential options when holding a pair and a singleton, with the singleton being suited to one of the cards in the pair. Having suited cards is disadvantageous since it lowers the probability of completing a flush with the pair. The table further confirms that retaining the pair significantly yields the best expected value.
Rank
| Singleton | Pair | Two | Singletons A |
K A |
|---|---|---|---|---|
| Q | A | 2.678 | 1.496 | 1.272 |
| J | A | 2.690 | 1.379 | 1.143 |
| A | A | 2.704 | 1.287 | 1.045 |
| A | 10 | 2.714 | 1.224 | 0.975 |
| A | 9 | 2.712 | 1.080 | 0.820 |
| A | 8 | 2.707 | 1.042 | 0.777 |
| A | 7 | 2.708 | 1.013 | 0.745 |
| A | 6 | 2.710 | 0.986 | 0.713 |
| A | 5 | 2.708 | 1.037 | 0.768 |
| K | 4 | 2.691 | 1.014 | 0.744 |
| A | 3 | 2.672 | 0.995 | 0.722 |
| K | 2 | 2.650 | 0.962 | 0.687 |
| Q | K | 2.378 | 1.485 | 1.250 |
| J | K | 2.205 | 1.300 | 1.072 |
| K | K | 2.214 | 1.221 | 0.986 |
| K | 10 | 2.222 | 1.168 | 0.926 |
| K | 9 | 2.223 | 1.026 | 0.773 |
| K | 8 | 2.224 | 0.936 | 0.675 |
| K | 7 | 2.224 | 0.915 | 0.652 |
| K | 6 | 2.226 | 0.899 | 0.635 |
| K | 5 | 2.226 | 0.884 | 0.618 |
| K | 4 | 2.210 | 0.863 | 0.594 |
| Q | 3 | 2.198 | 0.846 | 0.576 |
| A | 2 | 2.181 | 0.828 | 0.557 |
| Q | K | 1.984 | 1.367 | 1.119 |
| Q | J | 1.980 | 1.295 | 1.057 |
| Q | Q | 1.849 | 1.192 | 0.961 |
| Q | 10 | 1.858 | 1.145 | 0.911 |
| Q | 9 | 1.856 | 1.007 | 0.762 |
| Q | 8 | 1.858 | 0.921 | 0.668 |
| Q | 7 | 1.865 | 0.848 | 0.587 |
| Q | 6 | 1.858 | 0.834 | 0.573 |
| Q | 5 | 1.860 | 0.822 | 0.558 |
| Q | 4 | 1.854 | 0.803 | 0.539 |
| J | 3 | 1.841 | 0.787 | 0.521 |
| A | 2 | 1.828 | 0.769 | 0.503 |
| J | K | 1.686 | 1.280 | 1.024 |
| J | Q | 1.687 | 1.221 | 0.975 |
| J | J | 1.684 | 1.189 | 0.953 |
| J | 10 | 1.587 | 1.150 | 0.922 |
| J | 9 | 1.582 | 1.019 | 0.781 |
| J | 8 | 1.584 | 0.936 | 0.689 |
| J | 7 | 1.585 | 0.856 | 0.603 |
| J | 6 | 1.592 | 0.784 | 0.529 |
| J | 5 | 1.589 | 0.777 | 0.518 |
| J | 4 | 1.584 | 0.758 | 0.500 |
| A | 3 | 1.576 | 0.744 | 0.483 |
| K | 2 | 1.566 | 0.730 | 0.468 |
| 10 | Q | 1.459 | 1.220 | 0.957 |
| 10 | J | 1.454 | 1.169 | 0.917 |
| 10 | A | 1.456 | 1.144 | 0.901 |
| 10 | K | 1.456 | 1.145 | 0.912 |
| 10 | 9 | 1.371 | 1.048 | 0.816 |
| 10 | 8 | 1.372 | 0.962 | 0.724 |
| 10 | 7 | 1.374 | 0.885 | 0.641 |
| 10 | 6 | 1.378 | 0.813 | 0.562 |
| 10 | 5 | 1.383 | 0.744 | 0.490 |
| 10 | 4 | 1.374 | 0.733 | 0.476 |
| 10 | 3 | 1.369 | 0.717 | 0.460 |
| 10 | 2 | 1.364 | 0.703 | 0.447 |
| 9 | Q | 1.276 | 1.068 | 0.792 |
| 9 | J | 1.275 | 1.011 | 0.746 |
| 9 | A | 1.278 | 0.992 | 0.737 |
| 9 | K | 1.280 | 0.999 | 0.754 |
| 9 | 10 | 1.280 | 1.027 | 0.789 |
| 9 | 8 | 1.212 | 0.949 | 0.713 |
| 9 | 7 | 1.212 | 0.896 | 0.656 |
| 9 | 6 | 1.213 | 0.827 | 0.583 |
| 9 | 5 | 1.214 | 0.757 | 0.507 |
| 9 | 4 | 1.215 | 0.688 | 0.433 |
| 9 | 3 | 1.210 | 0.676 | 0.422 |
| 9 | 2 | 1.205 | 0.661 | 0.407 |
| 8 | Q | 1.148 | 1.029 | 0.748 |
| 8 | J | 1.149 | 0.923 | 0.652 |
| 8 | A | 1.154 | 0.902 | 0.639 |
| 8 | K | 1.155 | 0.911 | 0.658 |
| 8 | 10 | 1.153 | 0.939 | 0.695 |
| 8 | 9 | 1.150 | 0.934 | 0.694 |
| 8 | 7 | 1.099 | 0.915 | 0.678 |
| 8 | 6 | 1.101 | 0.866 | 0.627 |
| 8 | 5 | 1.102 | 0.799 | 0.556 |
| 8 | 4 | 1.100 | 0.722 | 0.474 |
| 8 | 3 | 1.097 | 0.653 | 0.401 |
| 8 | 2 | 1.094 | 0.644 | 0.394 |
| 7 | Q | 1.053 | 1.000 | 0.715 |
| 7 | J | 1.054 | 0.904 | 0.627 |
| 7 | A | 1.058 | 0.829 | 0.560 |
| 7 | K | 1.059 | 0.831 | 0.570 |
| 7 | 10 | 1.062 | 0.862 | 0.612 |
| 7 | 9 | 1.057 | 0.878 | 0.633 |
| 7 | 8 | 1.054 | 0.902 | 0.663 |
| 7 | 6 | 1.016 | 0.889 | 0.655 |
| 7 | 5 | 1.016 | 0.841 | 0.605 |
| 7 | 4 | 1.014 | 0.763 | 0.524 |
| 7 | 3 | 1.014 | 0.689 | 0.445 |
| 7 | 2 | 1.013 | 0.625 | 0.379 |
| 6 | Q | 0.984 | 0.975 | 0.688 |
| 6 | J | 0.985 | 0.888 | 0.610 |
| 6 | A | 0.988 | 0.820 | 0.549 |
| 6 | K | 0.991 | 0.768 | 0.503 |
| 6 | 10 | 0.992 | 0.785 | 0.529 |
| 6 | 9 | 0.988 | 0.808 | 0.558 |
| 6 | 8 | 0.988 | 0.848 | 0.606 |
| 6 | 7 | 0.986 | 0.877 | 0.641 |
| 6 | 5 | 0.953 | 0.868 | 0.637 |
| 6 | 4 | 0.952 | 0.811 | 0.577 |
| 6 | 3 | 0.950 | 0.737 | 0.500 |
| 6 | 2 | 0.949 | 0.663 | 0.424 |
| 5 | Q | 0.924 | 1.037 | 0.752 |
| 5 | J | 0.930 | 0.876 | 0.596 |
| 5 | A | 0.931 | 0.811 | 0.538 |
| 5 | K | 0.933 | 0.760 | 0.494 |
| 5 | 10 | 0.939 | 0.725 | 0.464 |
| 5 | 9 | 0.936 | 0.740 | 0.484 |
| 5 | 8 | 0.931 | 0.783 | 0.535 |
| 5 | 7 | 0.933 | 0.827 | 0.587 |
| 5 | 6 | 0.930 | 0.859 | 0.626 |
| 5 | 4 | 0.900 | 0.855 | 0.627 |
| 5 | 3 | 0.900 | 0.798 | 0.568 |
| 5 | 2 | 0.902 | 0.727 | 0.496 |
| 4 | Q | 0.876 | 1.011 | 0.726 |
| 4 | J | 0.880 | 0.856 | 0.573 |
| 4 | A | 0.884 | 0.792 | 0.516 |
| 4 | K | 0.885 | 0.742 | 0.473 |
| 4 | 10 | 0.886 | 0.712 | 0.449 |
| 4 | 9 | 0.888 | 0.670 | 0.410 |
| 4 | 8 | 0.887 | 0.704 | 0.452 |
| 4 | 7 | 0.886 | 0.749 | 0.505 |
| 4 | 6 | 0.884 | 0.796 | 0.561 |
| 4 | 5 | 0.883 | 0.848 | 0.618 |
| 4 | 3 | 0.859 | 0.759 | 0.530 |
| 4 | 2 | 0.858 | 0.704 | 0.474 |
| 3 | Q | 0.839 | 0.989 | 0.699 |
| 3 | J | 0.840 | 0.834 | 0.549 |
| 3 | Q | 0.846 | 0.771 | 0.494 |
| 3 | Q | 0.847 | 0.724 | 0.453 |
| 3 | 10 | 0.849 | 0.694 | 0.429 |
| 3 | 9 | 0.846 | 0.656 | 0.394 |
| 3 | 8 | 0.848 | 0.634 | 0.378 |
| 3 | 7 | 0.846 | 0.669 | 0.421 |
| 3 | 6 | 0.846 | 0.721 | 0.481 |
| 3 | 5 | 0.845 | 0.781 | 0.549 |
| 3 | 4 | 0.843 | 0.749 | 0.518 |
| 3 | 2 | 0.822 | 0.667 | 0.436 |
| 2 | Q | 0.811 | 0.954 | 0.660 |
| 2 | Q | 0.813 | 0.813 | 0.526 |
| 2 | Q | 0.816 | 0.751 | 0.472 |
| 2 | Q | 0.817 | 0.707 | 0.434 |
| 2 | 10 | 0.819 | 0.675 | 0.410 |
| 2 | 9 | 0.816 | 0.640 | 0.377 |
| 2 | 8 | 0.819 | 0.623 | 0.366 |
| 2 | 7 | 0.818 | 0.603 | 0.352 |
| 2 | 6 | 0.816 | 0.641 | 0.397 |
| 2 | 5 | 0.819 | 0.704 | 0.470 |
| 2 | 4 | 0.817 | 0.687 | 0.454 |
| 2 | 3 | 0.815 | 0.660 | 0.427 |
Q
This table outlines the expected returns for all three potential strategies when you have three suited singletons. Typically, the best play is to discard the lowest-ranked one. However, if all your cards hold low values, and the two lowest are close in rank while the highest is not, you might consider pursuing a straight by keeping the two lowest.
J
| A | J | K J Q |
J J J |
J J J |
|---|---|---|---|---|
| J | J | 1.541 | 1.443 | 1.405 |
| J | A | 1.550 | 1.325 | 1.305 |
| K | 10 | 1.550 | 1.240 | 1.230 |
| Q | 9 | 1.559 | 1.102 | 1.093 |
| J | 8 | 1.548 | 1.053 | 0.988 |
| A | 7 | 1.557 | 1.016 | 0.967 |
| K | 6 | 1.551 | 0.986 | 0.942 |
| Q | 5 | 1.559 | 1.031 | 0.924 |
| J | 4 | 1.554 | 1.012 | 0.903 |
| A | 3 | 1.543 | 0.987 | 0.885 |
| K | 2 | 1.536 | 0.955 | 0.865 |
| Q | J | 1.402 | 1.325 | 1.245 |
| A | 10 | 1.399 | 1.238 | 1.185 |
| K | 9 | 1.415 | 1.099 | 1.055 |
| Q | 8 | 1.414 | 1.054 | 0.957 |
| J | 7 | 1.412 | 1.018 | 0.885 |
| A | 6 | 1.417 | 0.987 | 0.870 |
| K | 5 | 1.418 | 1.032 | 0.852 |
| Q | 4 | 1.411 | 1.009 | 0.831 |
| J | 3 | 1.405 | 0.987 | 0.814 |
| A | 2 | 1.398 | 0.954 | 0.800 |
| K | 10 | 1.298 | 1.238 | 1.174 |
| Q | 9 | 1.307 | 1.099 | 1.048 |
| J | 8 | 1.306 | 1.052 | 0.952 |
| A | 7 | 1.305 | 1.021 | 0.877 |
| K | 6 | 1.307 | 0.990 | 0.813 |
| Q | 5 | 1.310 | 1.028 | 0.798 |
| J | 4 | 1.306 | 1.013 | 0.780 |
| A | 3 | 1.305 | 0.989 | 0.767 |
| K | 2 | 1.295 | 0.956 | 0.752 |
| Q | 9 | 1.228 | 1.099 | 1.068 |
| J | 8 | 1.229 | 1.054 | 0.979 |
| Q | 7 | 1.227 | 1.015 | 0.895 |
| Q | 6 | 1.233 | 0.992 | 0.828 |
| Q | 5 | 1.234 | 1.037 | 0.764 |
| Q | 4 | 1.229 | 1.010 | 0.747 |
| Q | 3 | 1.225 | 0.990 | 0.735 |
| Q | 2 | 1.223 | 0.959 | 0.722 |
| Q | 8 | 1.078 | 1.046 | 0.969 |
| J | 7 | 1.079 | 1.015 | 0.915 |
| A | 6 | 1.079 | 0.985 | 0.845 |
| J | 5 | 1.083 | 1.031 | 0.779 |
| K | 4 | 1.077 | 1.010 | 0.709 |
| J | 3 | 1.079 | 0.989 | 0.704 |
| Q | 2 | 1.070 | 0.951 | 0.686 |
| J | 7 | 1.032 | 1.010 | 0.926 |
| J | 6 | 1.031 | 0.982 | 0.880 |
| J | 5 | 1.034 | 1.026 | 0.814 |
| J | 4 | 1.037 | 1.011 | 0.739 |
| J | 3 | 1.034 | 0.990 | 0.679 |
| J | 2 | 1.025 | 0.953 | 0.670 |
| J | 6 | 0.997 | 0.978 | 0.904 |
| J | 7 | 1.000 | 1.028 | 0.854 |
| J | 7 | 1.003 | 1.009 | 0.783 |
| A | 3 | 0.998 | 0.988 | 0.710 |
| K | 2 | 0.996 | 0.962 | 0.650 |
| Q | 6 | 0.971 | 1.025 | 0.883 |
| J | 6 | 0.973 | 1.005 | 0.829 |
| A | 6 | 0.970 | 0.986 | 0.762 |
| K | 2 | 0.969 | 0.961 | 0.688 |
| Q | 4 | 1.003 | 0.990 | 0.855 |
| J | 3 | 1.003 | 0.971 | 0.800 |
| A | 2 | 1.001 | 0.944 | 0.731 |
| K | 3 | 0.981 | 0.967 | 0.766 |
| Q | 2 | 0.982 | 0.941 | 0.713 |
| J | 2 | 0.959 | 0.937 | 0.686 |
| A | K | 1.300 | 1.239 | 1.234 |
| Q | 10 | 1.303 | 1.166 | 1.170 |
| J | 9 | 1.316 | 1.030 | 1.045 |
| A | 8 | 1.324 | 0.950 | 0.961 |
| K | 7 | 1.321 | 0.923 | 0.878 |
| Q | 6 | 1.324 | 0.904 | 0.867 |
| J | 5 | 1.326 | 0.886 | 0.852 |
| A | 4 | 1.321 | 0.868 | 0.836 |
| K | 3 | 1.316 | 0.844 | 0.816 |
| Q | 2 | 1.309 | 0.829 | 0.801 |
| J | 10 | 1.216 | 1.170 | 1.159 |
| A | 9 | 1.227 | 1.033 | 1.038 |
| K | 8 | 1.239 | 0.953 | 0.964 |
| Q | 7 | 1.239 | 0.930 | 0.880 |
| J | 6 | 1.235 | 0.906 | 0.813 |
| A | 5 | 1.239 | 0.891 | 0.804 |
| K | 4 | 1.232 | 0.864 | 0.780 |
| Q | 3 | 1.227 | 0.849 | 0.769 |
| J | 2 | 1.223 | 0.830 | 0.752 |
| A | 9 | 1.156 | 1.027 | 1.046 |
| K | 8 | 1.172 | 0.952 | 0.981 |
| Q | 7 | 1.170 | 0.927 | 0.899 |
| J | 6 | 1.174 | 0.907 | 0.825 |
| A | 5 | 1.173 | 0.888 | 0.763 |
| K | 4 | 1.169 | 0.867 | 0.747 |
| Q | 3 | 1.167 | 0.851 | 0.736 |
| J | 2 | 1.164 | 0.831 | 0.721 |
| Pair with Suit Penalty | 8 | 1.017 | 0.946 | 0.976 |
| Dealt Three of Kind | 7 | 1.023 | 0.925 | 0.914 |
| Rank | 6 | 1.018 | 0.901 | 0.845 |
| Singleton | 5 | 1.023 | 0.888 | 0.779 |
| Pair | 4 | 1.023 | 0.869 | 0.714 |
| Suited | 3 | 1.016 | 0.849 | 0.701 |
| Singletons | 2 | 1.014 | 0.832 | 0.689 |
| Unsuited | Singletons | 0.931 | 0.917 | 0.933 |
| A | 6 | 0.931 | 0.897 | 0.882 |
| K | 5 | 0.935 | 0.884 | 0.816 |
| A | 4 | 0.934 | 0.866 | 0.745 |
| Q | 3 | 0.930 | 0.848 | 0.682 |
| A | 2 | 0.927 | 0.826 | 0.675 |
| J | 6 | 0.906 | 0.894 | 0.901 |
| A | 5 | 0.908 | 0.880 | 0.857 |
| A | 4 | 0.908 | 0.866 | 0.785 |
| A | 3 | 0.907 | 0.848 | 0.714 |
| A | 2 | 0.905 | 0.833 | 0.655 |
| A | 5 | 0.883 | 0.874 | 0.880 |
| A | 4 | 0.883 | 0.859 | 0.824 |
| A | 3 | 0.888 | 0.846 | 0.760 |
| A | 2 | 0.886 | 0.831 | 0.689 |
| A | K | 0.868 | 0.856 | 0.871 |
| A | 3 | 0.870 | 0.843 | 0.817 |
| K | 2 | 0.868 | 0.827 | 0.750 |
| Q | 3 | 0.850 | 0.840 | 0.784 |
| K | 2 | 0.847 | 0.822 | 0.728 |
| J | 2 | 0.828 | 0.818 | 0.699 |
| K | 10 | 1.156 | 1.119 | 1.142 |
| K | 9 | 1.174 | 0.995 | 1.022 |
| K | 8 | 1.181 | 0.914 | 0.948 |
| K | 7 | 1.199 | 0.859 | 0.881 |
| K | 6 | 1.191 | 0.842 | 0.810 |
| K | 5 | 1.198 | 0.826 | 0.801 |
| K | 4 | 1.190 | 0.806 | 0.781 |
| K | 3 | 1.186 | 0.786 | 0.763 |
| K | 2 | 1.182 | 0.775 | 0.755 |
| K | 9 | 1.114 | 0.993 | 1.034 |
| Q | 8 | 1.126 | 0.912 | 0.963 |
| A | 7 | 1.141 | 0.854 | 0.900 |
| Q | 6 | 1.143 | 0.841 | 0.824 |
| A | 5 | 1.139 | 0.825 | 0.763 |
| K | 4 | 1.140 | 0.808 | 0.746 |
| Q | 3 | 1.140 | 0.793 | 0.734 |
| J | 2 | 1.134 | 0.779 | 0.725 |
| A | 8 | 0.981 | 0.911 | 0.960 |
| K | 7 | 0.998 | 0.846 | 0.915 |
| Q | 6 | 0.997 | 0.840 | 0.841 |
| J | 5 | 0.997 | 0.826 | 0.777 |
| Pair with Suit Penalty | 4 | 0.999 | 0.810 | 0.712 |
| Dealt Three of Kind | 3 | 0.997 | 0.793 | 0.704 |
| Rank | 2 | 0.993 | 0.775 | 0.692 |
| Singleton | Pair | 0.906 | 0.843 | 0.938 |
| Suited | 6 | 0.910 | 0.833 | 0.883 |
| Singletons | 5 | 0.909 | 0.821 | 0.818 |
| Unsuited | 4 | 0.909 | 0.805 | 0.742 |
| Singletons | 3 | 0.908 | 0.792 | 0.682 |
| A | 2 | 0.906 | 0.773 | 0.672 |
| K | A | 0.837 | 0.833 | 0.913 |
| Q | A | 0.836 | 0.816 | 0.860 |
| J | 4 | 0.839 | 0.806 | 0.788 |
| A | 3 | 0.840 | 0.788 | 0.715 |
| A | 2 | 0.832 | 0.773 | 0.655 |
| A | A | 0.821 | 0.813 | 0.883 |
| A | A | 0.826 | 0.801 | 0.830 |
| A | 3 | 0.823 | 0.786 | 0.761 |
| A | 2 | 0.824 | 0.774 | 0.690 |
| A | K | 0.808 | 0.794 | 0.873 |
| A | K | 0.806 | 0.781 | 0.817 |
| Q | 2 | 0.808 | 0.770 | 0.750 |
| K | 3 | 0.789 | 0.782 | 0.785 |
| J | 2 | 0.789 | 0.768 | 0.732 |
| K | 2 | 0.777 | 0.767 | 0.703 |
| K | 9 | 1.094 | 0.979 | 1.021 |
| K | 8 | 1.112 | 0.911 | 0.955 |
| K | 7 | 1.122 | 0.839 | 0.886 |
| K | 6 | 1.140 | 0.792 | 0.829 |
| K | 5 | 1.136 | 0.781 | 0.762 |
| K | 4 | 1.132 | 0.763 | 0.745 |
| K | 3 | 1.132 | 0.749 | 0.730 |
| K | 2 | 1.129 | 0.734 | 0.721 |
| K | 8 | 0.974 | 0.903 | 0.946 |
| Q | 7 | 0.991 | 0.841 | 0.907 |
| A | 6 | 1.006 | 0.791 | 0.853 |
| Q | 5 | 1.000 | 0.778 | 0.777 |
| A | 4 | 1.000 | 0.764 | 0.711 |
| K | 3 | 0.997 | 0.744 | 0.700 |
| Q | 2 | 0.998 | 0.731 | 0.689 |
| J | A | 0.902 | 0.836 | 0.928 |
| K | 6 | 0.917 | 0.785 | 0.888 |
| Q | 5 | 0.920 | 0.776 | 0.817 |
| J | 4 | 0.918 | 0.758 | 0.741 |
| Pair with Suit Penalty | 3 | 0.913 | 0.743 | 0.679 |
| Dealt Three of Kind | 2 | 0.916 | 0.730 | 0.672 |
| Rank | Singleton | 0.836 | 0.781 | 0.913 |
| Pair | Suited | 0.838 | 0.771 | 0.858 |
| Singletons | 4 | 0.839 | 0.756 | 0.786 |
| Unsuited | 3 | 0.837 | 0.739 | 0.710 |
| Singletons | 2 | 0.839 | 0.734 | 0.655 |
| A | K | 0.778 | 0.773 | 0.890 |
| A | Q | 0.775 | 0.756 | 0.833 |
| A | 3 | 0.775 | 0.740 | 0.766 |
| J | 2 | 0.776 | 0.732 | 0.691 |
| A | A | 0.765 | 0.756 | 0.875 |
| A | A | 0.765 | 0.738 | 0.814 |
| A | 2 | 0.762 | 0.725 | 0.749 |
| A | A | 0.751 | 0.743 | 0.788 |
| A | 2 | 0.749 | 0.729 | 0.731 |
| A | 2 | 0.734 | 0.725 | 0.702 |
| K | 8 | 0.982 | 0.915 | 0.929 |
| A | 7 | 0.997 | 0.850 | 0.887 |
| K | 6 | 1.007 | 0.792 | 0.833 |
| Q | 5 | 1.025 | 0.744 | 0.780 |
| K | 4 | 1.023 | 0.733 | 0.710 |
| J | 3 | 1.017 | 0.715 | 0.696 |
| K | 2 | 1.018 | 0.705 | 0.687 |
| K | 7 | 0.916 | 0.852 | 0.911 |
| K | 6 | 0.932 | 0.792 | 0.873 |
| K | 5 | 0.942 | 0.743 | 0.817 |
| K | 4 | 0.938 | 0.729 | 0.737 |
| K | 3 | 0.943 | 0.722 | 0.680 |
| K | 2 | 0.938 | 0.705 | 0.670 |
| K | 10 | 0.853 | 0.788 | 0.901 |
| K | 5 | 0.863 | 0.736 | 0.858 |
| K | 4 | 0.864 | 0.728 | 0.783 |
| Q | 3 | 0.867 | 0.717 | 0.709 |
| A | 2 | 0.865 | 0.709 | 0.654 |
| Q | 10 | 0.793 | 0.738 | 0.892 |
| K | 10 | 0.792 | 0.727 | 0.827 |
| Q | 3 | 0.794 | 0.714 | 0.762 |
| J | 2 | 0.790 | 0.700 | 0.687 |
| Q | 10 | 0.733 | 0.724 | 0.876 |
| Q | 10 | 0.732 | 0.711 | 0.822 |
| Q | 10 | 0.733 | 0.700 | 0.753 |
| Q | 10 | 0.718 | 0.709 | 0.784 |
| Q | 10 | 0.720 | 0.700 | 0.734 |
| Q | 2 | 0.706 | 0.699 | 0.702 |
| Q | 7 | 0.898 | 0.856 | 0.897 |
| Q | 6 | 0.910 | 0.800 | 0.857 |
| Q | 5 | 0.925 | 0.748 | 0.806 |
| Q | 4 | 0.941 | 0.698 | 0.746 |
| J | 3 | 0.934 | 0.682 | 0.677 |
| A | 2 | 0.929 | 0.673 | 0.669 |
| J | 9 | 0.858 | 0.800 | 0.886 |
| K | 5 | 0.869 | 0.744 | 0.847 |
| J | 4 | 0.883 | 0.689 | 0.788 |
| Q | 3 | 0.881 | 0.680 | 0.710 |
| J | 2 | 0.879 | 0.670 | 0.651 |
| J | 9 | 0.802 | 0.743 | 0.881 |
| J | 9 | 0.816 | 0.690 | 0.831 |
| J | 3 | 0.814 | 0.680 | 0.759 |
| J | 2 | 0.816 | 0.668 | 0.688 |
| J | 9 | 0.748 | 0.689 | 0.882 |
| J | 9 | 0.746 | 0.676 | 0.817 |
| J | 9 | 0.750 | 0.669 | 0.752 |
| J | 9 | 0.683 | 0.676 | 0.792 |
| J | 9 | 0.685 | 0.668 | 0.736 |
| A | 9 | 0.672 | 0.666 | 0.704 |
| K | 8 | 0.864 | 0.825 | 0.869 |
| Q | 5 | 0.875 | 0.772 | 0.832 |
| J | 4 | 0.890 | 0.712 | 0.773 |
| A | 3 | 0.907 | 0.665 | 0.715 |
| K | 2 | 0.902 | 0.657 | 0.653 |
| Q | 8 | 0.831 | 0.771 | 0.866 |
| J | 4 | 0.842 | 0.710 | 0.816 |
| A | 3 | 0.855 | 0.661 | 0.762 |
| K | 2 | 0.855 | 0.654 | 0.689 |
| Q | 8 | 0.775 | 0.706 | 0.864 |
| J | 8 | 0.791 | 0.658 | 0.823 |
| A | 2 | 0.786 | 0.652 | 0.748 |
| K | 8 | 0.717 | 0.657 | 0.796 |
| Q | 8 | 0.717 | 0.652 | 0.733 |
| J | 8 | 0.653 | 0.652 | 0.709 |
| A | 7 | 0.841 | 0.802 | 0.849 |
| K | 4 | 0.852 | 0.740 | 0.800 |
| Q | 3 | 0.868 | 0.683 | 0.746 |
| J | 2 | 0.882 | 0.637 | 0.693 |
| A | 7 | 0.804 | 0.742 | 0.852 |
| K | 3 | 0.819 | 0.680 | 0.808 |
| Q | 2 | 0.836 | 0.636 | 0.753 |
| K | 7 | 0.754 | 0.685 | 0.784 |
| Q | 2 | 0.769 | 0.637 | 0.740 |
| J | 7 | 0.694 | 0.639 | 0.715 |
| Q | 6 | 0.823 | 0.777 | 0.832 |
| Q | 3 | 0.838 | 0.720 | 0.790 |
| Q | 2 | 0.851 | 0.665 | 0.738 |
| Q | 3 | 0.782 | 0.718 | 0.762 |
| Q | 2 | 0.796 | 0.662 | 0.720 |
| Q | 2 | 0.732 | 0.661 | 0.696 |
| Q | 3 | 0.810 | 0.759 | 0.742 |
| Q | 2 | 0.826 | 0.711 | 0.700 |
| Q | 2 | 0.772 | 0.709 | 0.677 |
| Q | 2 | 0.738 | 0.691 | 0.673 |
J
The following table shows the expected returns for all three potential plays when three unsuited singletons are dealt. Generally, the preferred move is to eliminate the lowest card. Nevertheless, if all the cards are low and the two lowest are closely ranked while the highest is further apart, you might choose to chase a straight using the two lowest cards.
A
| J | K | J Q J |
J J J |
J J J |
|---|---|---|---|---|
| J | J | 1.423 | 1.309 | 1.263 |
| J | A | 1.429 | 1.186 | 1.155 |
| K | 10 | 1.431 | 1.092 | 1.074 |
| Q | 9 | 1.443 | 0.943 | 0.924 |
| J | 8 | 1.438 | 0.888 | 0.814 |
| A | 7 | 1.441 | 0.846 | 0.781 |
| K | 6 | 1.440 | 0.814 | 0.756 |
| Q | 5 | 1.443 | 0.856 | 0.733 |
| J | 4 | 1.440 | 0.835 | 0.712 |
| A | 3 | 1.431 | 0.809 | 0.690 |
| K | 2 | 1.420 | 0.773 | 0.669 |
| Q | J | 1.272 | 1.186 | 1.099 |
| A | 10 | 1.273 | 1.091 | 1.028 |
| K | 9 | 1.288 | 0.940 | 0.890 |
| Q | 8 | 1.285 | 0.889 | 0.783 |
| J | 7 | 1.284 | 0.850 | 0.700 |
| A | 6 | 1.286 | 0.813 | 0.682 |
| K | 5 | 1.288 | 0.859 | 0.663 |
| Q | 4 | 1.284 | 0.834 | 0.642 |
| J | 3 | 1.279 | 0.811 | 0.622 |
| A | 2 | 1.271 | 0.777 | 0.607 |
| K | 10 | 1.154 | 1.091 | 1.017 |
| Q | 9 | 1.169 | 0.941 | 0.890 |
| K | 8 | 1.169 | 0.888 | 0.785 |
| Q | 7 | 1.169 | 0.850 | 0.697 |
| J | 6 | 1.169 | 0.819 | 0.626 |
| Q | 5 | 1.172 | 0.861 | 0.611 |
| Q | 4 | 1.170 | 0.838 | 0.591 |
| Q | 3 | 1.164 | 0.812 | 0.572 |
| Q | 2 | 1.156 | 0.778 | 0.558 |
| Q | 9 | 1.080 | 0.941 | 0.905 |
| Q | 8 | 1.080 | 0.888 | 0.809 |
| Q | 7 | 1.079 | 0.848 | 0.721 |
| Q | 6 | 1.082 | 0.818 | 0.643 |
| Q | 5 | 1.086 | 0.866 | 0.576 |
| Q | 4 | 1.083 | 0.838 | 0.558 |
| J | 3 | 1.078 | 0.811 | 0.542 |
| A | 2 | 1.072 | 0.778 | 0.528 |
| J | 8 | 0.915 | 0.880 | 0.805 |
| K | 7 | 0.916 | 0.842 | 0.741 |
| J | 6 | 0.917 | 0.811 | 0.666 |
| Q | 5 | 0.921 | 0.860 | 0.592 |
| J | 4 | 0.919 | 0.837 | 0.521 |
| J | 3 | 0.916 | 0.809 | 0.508 |
| J | 2 | 0.910 | 0.774 | 0.494 |
| J | 7 | 0.862 | 0.838 | 0.757 |
| J | 6 | 0.864 | 0.809 | 0.705 |
| J | 5 | 0.870 | 0.858 | 0.632 |
| J | 4 | 0.868 | 0.834 | 0.553 |
| J | 3 | 0.866 | 0.815 | 0.487 |
| J | 2 | 0.863 | 0.775 | 0.479 |
| J | 6 | 0.827 | 0.805 | 0.729 |
| A | 7 | 0.830 | 0.855 | 0.677 |
| K | 7 | 0.829 | 0.832 | 0.603 |
| Q | 3 | 0.828 | 0.811 | 0.523 |
| J | 2 | 0.827 | 0.782 | 0.463 |
| A | 6 | 0.798 | 0.857 | 0.710 |
| K | 6 | 0.796 | 0.835 | 0.652 |
| Q | 6 | 0.795 | 0.811 | 0.581 |
| J | 2 | 0.796 | 0.781 | 0.505 |
| A | 4 | 0.830 | 0.814 | 0.680 |
| K | 3 | 0.827 | 0.791 | 0.624 |
| Q | 2 | 0.827 | 0.762 | 0.554 |
| J | 3 | 0.804 | 0.789 | 0.591 |
| A | 2 | 0.803 | 0.760 | 0.537 |
| K | 2 | 0.782 | 0.758 | 0.508 |
| Q | J | 1.166 | 1.093 | 1.081 |
| A | 10 | 1.165 | 1.013 | 1.011 |
| K | 9 | 1.183 | 0.869 | 0.873 |
| Q | 8 | 1.195 | 0.782 | 0.787 |
| J | 7 | 1.195 | 0.753 | 0.700 |
| A | 6 | 1.194 | 0.727 | 0.683 |
| K | 5 | 1.193 | 0.707 | 0.665 |
| Q | 4 | 1.190 | 0.685 | 0.644 |
| J | 3 | 1.185 | 0.665 | 0.625 |
| A | 2 | 1.180 | 0.647 | 0.610 |
| K | 10 | 1.065 | 1.013 | 1.002 |
| Q | 9 | 1.082 | 0.870 | 0.872 |
| J | 8 | 1.096 | 0.783 | 0.789 |
| A | 7 | 1.095 | 0.752 | 0.695 |
| K | 6 | 1.094 | 0.731 | 0.625 |
| Q | 5 | 1.095 | 0.707 | 0.611 |
| J | 4 | 1.093 | 0.686 | 0.592 |
| A | 3 | 1.089 | 0.666 | 0.575 |
| K | 2 | 1.083 | 0.646 | 0.559 |
| Q | 9 | 1.009 | 0.868 | 0.890 |
| J | 8 | 1.023 | 0.780 | 0.813 |
| Three Suited Singletons | 7 | 1.021 | 0.751 | 0.721 |
| Three Suited Singletons | 6 | 1.023 | 0.730 | 0.642 |
| Hand | 5 | 1.023 | 0.712 | 0.576 |
| Discard | 4 | 1.023 | 0.688 | 0.560 |
| Expected | 3 | 1.018 | 0.666 | 0.544 |
| Return | 2 | 1.013 | 0.646 | 0.530 |
| Middle and High | 8 | 0.857 | 0.778 | 0.810 |
| Expected | 7 | 0.856 | 0.747 | 0.740 |
| Return | 6 | 0.859 | 0.726 | 0.666 |
| Low and High | 5 | 0.860 | 0.709 | 0.593 |
| Expected | 4 | 0.857 | 0.687 | 0.523 |
| Return | 3 | 0.856 | 0.664 | 0.511 |
| Low and Middle | 2 | 0.851 | 0.645 | 0.499 |
| A-K-Q | Q | 0.761 | 0.743 | 0.767 |
| A-K-J | 6 | 0.761 | 0.723 | 0.710 |
| J | 5 | 0.764 | 0.704 | 0.637 |
| A-K-10 | 4 | 0.762 | 0.683 | 0.558 |
| A-K-9 | 3 | 0.761 | 0.665 | 0.493 |
| A-K-8 | 2 | 0.759 | 0.643 | 0.483 |
| A-K-7 | 6 | 0.732 | 0.721 | 0.731 |
| A-K-6 | 5 | 0.732 | 0.703 | 0.680 |
| A-K-5 | 4 | 0.734 | 0.682 | 0.605 |
| A-K-4 | 3 | 0.733 | 0.664 | 0.528 |
| A-K-3 | 2 | 0.731 | 0.647 | 0.465 |
| A-K-2 | A-Q-J | 0.708 | 0.698 | 0.712 |
| J | 4 | 0.708 | 0.679 | 0.653 |
| A-Q-10 | 3 | 0.709 | 0.663 | 0.581 |
| A-Q-9 | 2 | 0.711 | 0.646 | 0.506 |
| A-Q-8 | A-Q-7 | 0.690 | 0.676 | 0.701 |
| A-Q-6 | 3 | 0.689 | 0.657 | 0.643 |
| A-Q-5 | 2 | 0.689 | 0.641 | 0.572 |
| A-Q-4 | 3 | 0.668 | 0.656 | 0.610 |
| A-Q-3 | 2 | 0.667 | 0.639 | 0.555 |
| A-Q-2 | 2 | 0.649 | 0.637 | 0.526 |
| A-J-10 | 10 | 1.005 | 0.964 | 0.984 |
| A-J-9 | 9 | 1.024 | 0.829 | 0.855 |
| A-J-8 | 8 | 1.038 | 0.745 | 0.773 |
| A-J-7 | 7 | 1.054 | 0.678 | 0.701 |
| A-J-6 | 6 | 1.051 | 0.662 | 0.624 |
| A-J-5 | 5 | 1.054 | 0.643 | 0.610 |
| A-J-4 | 4 | 1.051 | 0.624 | 0.592 |
| A-J-3 | 3 | 1.046 | 0.605 | 0.574 |
| A-J-2 | 2 | 1.043 | 0.589 | 0.559 |
| A-10-9 | 9 | 0.961 | 0.827 | 0.872 |
| A-10-8 | 8 | 0.978 | 0.744 | 0.796 |
| A-10-7 | 7 | 0.993 | 0.677 | 0.726 |
| A-10-6 | 6 | 0.992 | 0.662 | 0.640 |
| A-10-5 | 5 | 0.993 | 0.647 | 0.574 |
| A-10-4 | 4 | 0.992 | 0.624 | 0.558 |
| A-10-3 | 3 | 0.989 | 0.607 | 0.544 |
| A-10-2 | 2 | 0.985 | 0.589 | 0.529 |
| A-9-8 | 8 | 0.819 | 0.740 | 0.795 |
| A-9-7 | 7 | 0.835 | 0.675 | 0.746 |
| A-9-6 | 6 | 0.836 | 0.660 | 0.667 |
| A-9-5 | 5 | 0.836 | 0.644 | 0.591 |
| A-9-4 | 4 | 0.835 | 0.626 | 0.522 |
| A-9-3 | 3 | 0.835 | 0.605 | 0.511 |
| A-9-2 | 2 | 0.831 | 0.590 | 0.497 |
| A-8-7 | A-8-6 | 0.740 | 0.671 | 0.770 |
| A-8-5 | 6 | 0.739 | 0.655 | 0.708 |
| A-8-4 | 5 | 0.739 | 0.640 | 0.636 |
| A-8-3 | 4 | 0.741 | 0.624 | 0.558 |
| A-8-2 | 3 | 0.740 | 0.607 | 0.492 |
| A-7-6 | 2 | 0.737 | 0.586 | 0.482 |
| A-7-5 | A-7-4 | 0.660 | 0.654 | 0.741 |
| A-7-3 | A-7-2 | 0.662 | 0.640 | 0.685 |
| A-6-5 | 4 | 0.662 | 0.620 | 0.608 |
| A-6-4 | 3 | 0.663 | 0.606 | 0.531 |
| A-6-3 | 2 | 0.662 | 0.590 | 0.469 |
| A-6-2 | A-5-4 | 0.644 | 0.636 | 0.712 |
| A-5-3 | A-5-2 | 0.646 | 0.618 | 0.654 |
| A-4-3 | 3 | 0.646 | 0.603 | 0.582 |
| A-4-2 | 2 | 0.647 | 0.588 | 0.507 |
| A-3-2 | K-Q-J | 0.628 | 0.616 | 0.700 |
| J | K-Q-10 | 0.628 | 0.598 | 0.645 |
| K-Q-9 | 2 | 0.629 | 0.584 | 0.573 |
| K-Q-8 | K-Q-7 | 0.608 | 0.597 | 0.612 |
| K-Q-6 | 2 | 0.608 | 0.582 | 0.556 |
| K-Q-5 | 2 | 0.593 | 0.583 | 0.526 |
| K-Q-4 | 9 | 0.943 | 0.815 | 0.857 |
| K-Q-3 | 8 | 0.958 | 0.734 | 0.778 |
| K-Q-2 | 7 | 0.975 | 0.667 | 0.710 |
| K-J-10 | 6 | 0.992 | 0.610 | 0.648 |
| K-J-9 | 5 | 0.992 | 0.597 | 0.574 |
| K-J-8 | 4 | 0.988 | 0.575 | 0.557 |
| K-J-7 | 3 | 0.987 | 0.559 | 0.541 |
| K-J-6 | 2 | 0.984 | 0.545 | 0.528 |
| K-J-5 | 8 | 0.812 | 0.734 | 0.778 |
| K-J-4 | 7 | 0.828 | 0.665 | 0.730 |
| K-J-3 | 6 | 0.843 | 0.607 | 0.671 |
| K-J-2 | 5 | 0.842 | 0.596 | 0.591 |
| K-10-9 | 4 | 0.844 | 0.579 | 0.521 |
| K-10-8 | 3 | 0.841 | 0.559 | 0.508 |
| K-10-7 | 2 | 0.839 | 0.544 | 0.496 |
| K-10-6 | K-10-5 | 0.734 | 0.663 | 0.756 |
| K-10-4 | 6 | 0.750 | 0.605 | 0.715 |
| K-10-3 | 5 | 0.750 | 0.594 | 0.635 |
| K-10-2 | 4 | 0.749 | 0.577 | 0.556 |
| K-9-8 | 3 | 0.750 | 0.562 | 0.492 |
| K-9-7 | 2 | 0.749 | 0.545 | 0.482 |
| K-9-6 | K-9-5 | 0.664 | 0.602 | 0.746 |
| K-9-4 | K-9-3 | 0.662 | 0.590 | 0.684 |
| K-9-2 | 4 | 0.667 | 0.575 | 0.607 |
| K-8-7 | 3 | 0.667 | 0.560 | 0.530 |
| K | 2 | 0.666 | 0.548 | 0.468 |
| K-8-6 | K-8-5 | 0.595 | 0.590 | 0.721 |
| K-8-4 | K-8-3 | 0.596 | 0.574 | 0.658 |
| K-8-2 | 3 | 0.597 | 0.559 | 0.586 |
| K-7-6 | 2 | 0.598 | 0.545 | 0.510 |
| K-7-5 | K-7-4 | 0.581 | 0.569 | 0.701 |
| K-7-3 | K-7-2 | 0.584 | 0.556 | 0.646 |
| K-6-5 | 2 | 0.585 | 0.543 | 0.574 |
| K-6-4 | K-6-3 | 0.565 | 0.555 | 0.613 |
| K-6-2 | 2 | 0.565 | 0.542 | 0.556 |
| K-5-4 | 2 | 0.549 | 0.540 | 0.526 |
| K | 8 | 0.821 | 0.746 | 0.762 |
| K-5-3 | 7 | 0.836 | 0.678 | 0.712 |
| K-5-2 | 6 | 0.854 | 0.615 | 0.655 |
| K-4-3 | 5 | 0.868 | 0.563 | 0.594 |
| K-4-2 | 4 | 0.866 | 0.548 | 0.520 |
| K-3-2 | 3 | 0.867 | 0.529 | 0.507 |
| Q-J-10 | 2 | 0.865 | 0.517 | 0.494 |
| Q-J-9 | 7 | 0.749 | 0.677 | 0.739 |
| Q-J-8 | 6 | 0.763 | 0.614 | 0.698 |
| Q-J-7 | 5 | 0.780 | 0.561 | 0.642 |
| Q-J-6 | 4 | 0.779 | 0.547 | 0.555 |
| Q-J-5 | 3 | 0.780 | 0.534 | 0.489 |
| Q-J-4 | 2 | 0.779 | 0.518 | 0.481 |
| Q-J-3 | 10 | 0.681 | 0.612 | 0.730 |
| Q-J-2 | 5 | 0.696 | 0.559 | 0.688 |
| Q-10-9 | 4 | 0.696 | 0.546 | 0.606 |
| Q-10-8 | 3 | 0.697 | 0.533 | 0.527 |
| Q-10-7 | 2 | 0.697 | 0.522 | 0.466 |
| Q-10-6 | 10 | 0.619 | 0.558 | 0.725 |
| Q-10-5 | 10 | 0.616 | 0.543 | 0.657 |
| Q-10-4 | 3 | 0.619 | 0.531 | 0.585 |
| Q-10-3 | 2 | 0.619 | 0.520 | 0.508 |
| Q-10-2 | 10 | 0.552 | 0.541 | 0.708 |
| Q-9-8 | 10 | 0.553 | 0.527 | 0.649 |
| Q-9-7 | 10 | 0.553 | 0.516 | 0.576 |
| Q-9-6 | 10 | 0.538 | 0.528 | 0.612 |
| Q-9-5 | 10 | 0.537 | 0.516 | 0.557 |
| Q-9-4 | 10 | 0.525 | 0.516 | 0.528 |
| Q-9-3 | 7 | 0.725 | 0.680 | 0.721 |
| Q-9-2 | 6 | 0.741 | 0.622 | 0.679 |
| Q-8-7 | 5 | 0.756 | 0.564 | 0.623 |
| Q | 4 | 0.773 | 0.508 | 0.559 |
| Q-8-6 | 3 | 0.774 | 0.498 | 0.487 |
| Q-8-5 | 2 | 0.772 | 0.483 | 0.477 |
| Q-8-4 | 9 | 0.682 | 0.620 | 0.710 |
| Q-8-3 | 5 | 0.698 | 0.562 | 0.670 |
| Q-8-2 | 4 | 0.715 | 0.506 | 0.611 |
| Q-7-6 | 3 | 0.716 | 0.497 | 0.526 |
| Q | 2 | 0.716 | 0.486 | 0.464 |
| Q-7-5 | 9 | 0.626 | 0.560 | 0.709 |
| Q | 9 | 0.644 | 0.505 | 0.662 |
| Q-7-4 | 3 | 0.643 | 0.495 | 0.583 |
| Q-7-3 | 2 | 0.645 | 0.482 | 0.506 |
| Q-7-2 | 9 | 0.568 | 0.502 | 0.711 |
| Q-6-5 | 9 | 0.569 | 0.492 | 0.647 |
| Q | 9 | 0.572 | 0.483 | 0.575 |
| Q-6-4 | 9 | 0.501 | 0.493 | 0.618 |
| Q | 9 | 0.501 | 0.483 | 0.561 |
| Q-6-3 | 9 | 0.490 | 0.481 | 0.526 |
| Q-6-2 | 8 | 0.692 | 0.650 | 0.694 |
| Q-5-4 | 5 | 0.705 | 0.594 | 0.652 |
| Q | 4 | 0.725 | 0.530 | 0.593 |
| Q-5-3 | 3 | 0.742 | 0.479 | 0.531 |
| Q | 2 | 0.739 | 0.471 | 0.461 |
| Q-5-2 | 8 | 0.654 | 0.592 | 0.692 |
| Q-4-3 | 4 | 0.672 | 0.528 | 0.644 |
| Q-4-2 | 3 | 0.690 | 0.477 | 0.589 |
| Q-3-2 | 2 | 0.690 | 0.469 | 0.503 |
| J-10-9 | 8 | 0.601 | 0.527 | 0.695 |
| J-10-8 | 8 | 0.618 | 0.476 | 0.652 |
| J-10-7 | 2 | 0.618 | 0.468 | 0.572 |
| J-10-6 | 8 | 0.540 | 0.476 | 0.623 |
| J-10-5 | 8 | 0.539 | 0.470 | 0.559 |
| J-10-4 | 8 | 0.474 | 0.469 | 0.534 |
| J-10-3 | 7 | 0.667 | 0.625 | 0.674 |
| J-10-2 | 4 | 0.685 | 0.565 | 0.627 |
| J-9-8 | 3 | 0.704 | 0.504 | 0.571 |
| J-9-7 | 2 | 0.719 | 0.455 | 0.510 |
| J-9-6 | 7 | 0.632 | 0.562 | 0.678 |
| J-9-5 | 3 | 0.650 | 0.501 | 0.635 |
| J-9-4 | 2 | 0.668 | 0.452 | 0.579 |
| J-9-3 | 7 | 0.576 | 0.502 | 0.607 |
| J-9-2 | 2 | 0.592 | 0.454 | 0.563 |
| J-8-7 | 7 | 0.517 | 0.456 | 0.539 |
| J | 6 | 0.651 | 0.598 | 0.662 |
| J-8-6 | 3 | 0.669 | 0.541 | 0.616 |
| J-8-5 | 2 | 0.685 | 0.482 | 0.561 |
| J-8-4 | 3 | 0.611 | 0.543 | 0.588 |
| J-8-3 | 2 | 0.629 | 0.483 | 0.546 |
| J-8-2 | 2 | 0.558 | 0.486 | 0.522 |
| J-7-6 | 3 | 0.640 | 0.588 | 0.566 |
| J | 2 | 0.658 | 0.533 | 0.521 |
| J-7-5 | 2 | 0.602 | 0.535 | 0.498 |
| J | 2 | 0.572 | 0.519 | 0.500 |
Three Singletons — Lowest Two of the Same Suit
The upcoming table presents the expected returns for each of the three potential discards when you have three singletons, specifically when the two lowest cards match in suit. In 60.5% of situations, the optimal move is to retain the suited cards and throw away the highest-ranked one. In the remaining instances, you would discard the lowest card. The subsequent table illustrates the expected returns for all three possible selections among the three cards.
Three Singletons — Lowest Two of the Same Suit
| J-7-4 | J-7-3 | J-7-2 J-6-5 J |
J-6-4 J J-6-3 |
J-6-2 J-5-4 J |
|---|---|---|---|---|
| J-5-3 | J | 1.404 | 1.296 | 1.480 |
| J-5-2 | J-4-3 | 1.407 | 1.175 | 1.379 |
| J | 10 | 1.408 | 1.082 | 1.304 |
| J-4-2 | 9 | 1.421 | 0.936 | 1.168 |
| J-3-2 | 8 | 1.419 | 0.884 | 1.068 |
| 10-9-8 | 7 | 1.419 | 0.840 | 1.037 |
| 10-9-7 | 6 | 1.419 | 0.808 | 1.015 |
| 10-9-6 | 5 | 1.421 | 0.853 | 0.995 |
| 10-9-5 | 4 | 1.416 | 0.829 | 0.976 |
| 10-9-4 | 3 | 1.409 | 0.805 | 0.953 |
| 10-9-3 | 2 | 1.396 | 0.770 | 0.934 |
| 10-9-2 | 10-8-7 | 1.255 | 1.175 | 1.317 |
| 10-8-6 | 10 | 1.257 | 1.081 | 1.255 |
| 10-8-5 | 9 | 1.269 | 0.933 | 1.129 |
| 10-8-4 | 8 | 1.268 | 0.884 | 1.030 |
| 10-8-3 | 7 | 1.268 | 0.845 | 0.953 |
| 10-8-2 | 6 | 1.269 | 0.809 | 0.939 |
| 10-7-6 | 5 | 1.271 | 0.856 | 0.923 |
| 10-7-5 | 4 | 1.269 | 0.833 | 0.904 |
| 10-7-4 | 3 | 1.262 | 0.809 | 0.886 |
| 10-7-3 | 2 | 1.252 | 0.773 | 0.868 |
| 10-7-2 | 10-6-5 | 1.140 | 1.082 | 1.238 |
| 10-6-4 | 9 | 1.156 | 0.936 | 1.122 |
| 10-6-3 | 8 | 1.155 | 0.883 | 1.024 |
| 10-6-2 | 7 | 1.157 | 0.845 | 0.945 |
| 10-5-4 | 6 | 1.154 | 0.814 | 0.879 |
| 10-5-3 | 5 | 1.160 | 0.857 | 0.866 |
| 10-5-2 | 4 | 1.156 | 0.833 | 0.848 |
| 10-4-3 | 3 | 1.150 | 0.809 | 0.831 |
| 10-4-2 | 2 | 1.143 | 0.775 | 0.818 |
| 10-3-2 | 9-8-7 | 1.068 | 0.935 | 1.131 |
| 9-8-6 | 8 | 1.070 | 0.881 | 1.041 |
| 9-8-5 | 7 | 1.067 | 0.843 | 0.962 |
| 9-8-4 | 6 | 1.069 | 0.812 | 0.888 |
| 9-8-3 | 5 | 1.074 | 0.861 | 0.824 |
| 9-8-2 | 4 | 1.071 | 0.834 | 0.811 |
| 9-7-6 | 3 | 1.068 | 0.809 | 0.796 |
| 9-7-5 | 2 | 1.061 | 0.775 | 0.782 |
| 9-7-4 | 9-7-3 | 0.904 | 0.875 | 1.034 |
| 9-7-2 | 9-6-5 | 0.906 | 0.836 | 0.975 |
| 9-6-4 | 6 | 0.908 | 0.807 | 0.905 |
| 9-6-3 | 5 | 0.912 | 0.856 | 0.838 |
| 9-6-2 | 4 | 0.911 | 0.834 | 0.773 |
| 9-5-4 | 3 | 0.906 | 0.805 | 0.760 |
| 9-5-3 | 2 | 0.902 | 0.772 | 0.751 |
| 9-5-2 | 9-4-3 | 0.855 | 0.835 | 0.987 |
| 9-4-2 | 9-3-2 | 0.856 | 0.805 | 0.939 |
| 8-7-6 | 8-7-5 | 0.862 | 0.853 | 0.873 |
| 8-7-4 | 4 | 0.862 | 0.832 | 0.799 |
| 8-7-3 | 3 | 0.857 | 0.810 | 0.734 |
| 8-7-2 | 2 | 0.854 | 0.772 | 0.726 |
| 8-6-5 | 8-6-4 | 0.820 | 0.802 | 0.958 |
| 8-6-3 | 8-6-2 | 0.821 | 0.849 | 0.908 |
| 8-5-4 | 8-5-3 | 0.821 | 0.828 | 0.839 |
| 8-5-2 | 3 | 0.821 | 0.807 | 0.764 |
| 8-4-3 | 2 | 0.819 | 0.778 | 0.705 |
| 8-4-2 | 8-3-2 | 0.791 | 0.853 | 0.937 |
| 7-6-5 | 7-6-4 | 0.789 | 0.827 | 0.880 |
| 7-6-3 | 7-6-2 | 0.789 | 0.807 | 0.814 |
| 7-5-4 | 2 | 0.790 | 0.779 | 0.742 |
| 7-5-3 | 7-5-2 | 0.824 | 0.810 | 0.906 |
| 7-4-3 | 7-4-2 | 0.822 | 0.787 | 0.849 |
| 7-3-2 | 2 | 0.823 | 0.760 | 0.784 |
| 6-5-4 | 6-5-3 | 0.799 | 0.786 | 0.818 |
| 6-5-2 | 2 | 0.801 | 0.758 | 0.764 |
| 6-4-3 | 2 | 0.778 | 0.753 | 0.735 |
| 6-4-2 | 6-3-2 | 1.148 | 1.082 | 1.300 |
| 5-4-3 | 5-4-2 | 1.148 | 1.005 | 1.238 |
| 5-3-2 | 9 | 1.164 | 0.862 | 1.114 |
| 4-3-2 | 8 | 1.177 | 0.776 | 1.032 |
| Three Unsuited Singletons | 7 | 1.175 | 0.748 | 0.953 |
| Three Unsuited Singletons | 6 | 1.178 | 0.723 | 0.938 |
| Hand | 5 | 1.177 | 0.705 | 0.923 |
| Discard | 4 | 1.171 | 0.680 | 0.906 |
| Expected | 3 | 1.171 | 0.664 | 0.885 |
| Return | 2 | 1.161 | 0.642 | 0.870 |
| Middle and High | Expected | 1.054 | 1.005 | 1.223 |
| Return | Low and High | 1.069 | 0.861 | 1.105 |
| Expected | 8 | 1.081 | 0.776 | 1.031 |
| Return | 7 | 1.084 | 0.749 | 0.944 |
| Low and Middle | 6 | 1.080 | 0.726 | 0.879 |
| A-K-Q | 5 | 1.083 | 0.705 | 0.867 |
| Q | 4 | 1.079 | 0.682 | 0.849 |
| A-K-J | 3 | 1.077 | 0.663 | 0.833 |
| J | 2 | 1.068 | 0.643 | 0.819 |
| A-K-10 | A-K-9 | 0.996 | 0.861 | 1.116 |
| A-K-8 | A-K-7 | 1.011 | 0.774 | 1.044 |
| A-K-6 | 7 | 1.011 | 0.748 | 0.960 |
| A-K-5 | 6 | 1.014 | 0.727 | 0.889 |
| A-K-4 | 5 | 1.011 | 0.707 | 0.828 |
| A-K-3 | 4 | 1.011 | 0.684 | 0.814 |
| A-K-2 | 3 | 1.007 | 0.663 | 0.798 |
| A-Q-J | 2 | 1.001 | 0.643 | 0.783 |
| J | A-Q-10 | 0.846 | 0.769 | 1.038 |
| A-Q-9 | A-Q-8 | 0.849 | 0.744 | 0.976 |
| A-Q-7 | A-Q-6 | 0.849 | 0.722 | 0.907 |
| A-Q-5 | 5 | 0.851 | 0.705 | 0.840 |
| A-Q-4 | 4 | 0.848 | 0.683 | 0.775 |
| A-Q-3 | 3 | 0.848 | 0.663 | 0.763 |
| A-Q-2 | 2 | 0.844 | 0.643 | 0.751 |
| A-J-10 | A-J-9 | 0.751 | 0.737 | 0.994 |
| A-J-8 | A-J-7 | 0.752 | 0.716 | 0.943 |
| A-J-6 | A-J-5 | 0.756 | 0.698 | 0.877 |
| A-J-4 | A-J-3 | 0.757 | 0.682 | 0.803 |
| A-J-2 | 3 | 0.753 | 0.662 | 0.741 |
| A-10-9 | 2 | 0.749 | 0.639 | 0.732 |
| A-10-8 | A-10-7 | 0.725 | 0.717 | 0.961 |
| A-10-6 | A-10-5 | 0.727 | 0.699 | 0.911 |
| A-10-4 | A-10-3 | 0.727 | 0.680 | 0.840 |
| A-10-2 | A-9-8 | 0.728 | 0.662 | 0.768 |
| A-9-7 | 2 | 0.727 | 0.645 | 0.709 |
| A-9-6 | A-9-5 | 0.704 | 0.695 | 0.940 |
| A-9-4 | A-9-3 | 0.703 | 0.676 | 0.883 |
| A-9-2 | A-8-7 | 0.703 | 0.659 | 0.815 |
| A-8-6 | A-8-5 | 0.703 | 0.641 | 0.745 |
| A-8-4 | A-8-3 | 0.683 | 0.671 | 0.925 |
| A-8-2 | A-7-6 | 0.684 | 0.653 | 0.868 |
| A-7-5 | A-7-4 | 0.683 | 0.636 | 0.801 |
| A-7-3 | A-7-2 | 0.664 | 0.651 | 0.837 |
| A-6-5 | A-6-4 | 0.663 | 0.635 | 0.782 |
| A-6-3 | A-6-2 | 0.645 | 0.633 | 0.750 |
| A-5-4 | A-5-3 | 0.994 | 0.956 | 1.205 |
| A-5-2 | A-4-3 | 1.011 | 0.822 | 1.089 |
| A-4-2 | 8 | 1.026 | 0.738 | 1.013 |
| A-3-2 | 7 | 1.041 | 0.674 | 0.948 |
| K-Q-J | 6 | 1.041 | 0.658 | 0.877 |
| J | 5 | 1.041 | 0.641 | 0.866 |
| K-Q-10 | 4 | 1.039 | 0.621 | 0.850 |
| K-Q-9 | 3 | 1.034 | 0.601 | 0.834 |
| K-Q-8 | 2 | 1.030 | 0.585 | 0.818 |
| K-Q-7 | K-Q-6 | 0.953 | 0.822 | 1.101 |
| K-Q-5 | K-Q-4 | 0.965 | 0.737 | 1.029 |
| K-Q-3 | 7 | 0.982 | 0.672 | 0.964 |
| K-Q-2 | 6 | 0.981 | 0.658 | 0.886 |
| K-J-10 | 5 | 0.982 | 0.645 | 0.825 |
| K-J-9 | 4 | 0.980 | 0.619 | 0.813 |
| K-J-8 | 3 | 0.977 | 0.603 | 0.796 |
| K-J-7 | 2 | 0.974 | 0.586 | 0.781 |
| K-J-6 | K-J-5 | 0.812 | 0.737 | 1.027 |
| K-J-4 | K-J-3 | 0.826 | 0.669 | 0.980 |
| K-J-2 | K-10-9 | 0.826 | 0.655 | 0.906 |
| K-10-8 | K-10-7 | 0.827 | 0.640 | 0.838 |
| K-10-6 | 4 | 0.828 | 0.622 | 0.774 |
| K-10-5 | 3 | 0.827 | 0.603 | 0.763 |
| K-10-4 | 2 | 0.823 | 0.587 | 0.750 |
| K-10-3 | K-10-2 | 0.729 | 0.665 | 0.999 |
| K-9-8 | K-9-7 | 0.732 | 0.651 | 0.943 |
| K-9-6 | K-9-5 | 0.732 | 0.637 | 0.873 |
| K-9-4 | K-9-3 | 0.733 | 0.620 | 0.803 |
| K-9-2 | K-8-7 | 0.734 | 0.605 | 0.741 |
| K | K-8-6 | 0.730 | 0.586 | 0.731 |
| K-8-5 | K-8-4 | 0.651 | 0.647 | 0.968 |
| K-8-3 | K-8-2 | 0.652 | 0.633 | 0.917 |
| K-7-6 | K-7-5 | 0.656 | 0.618 | 0.846 |
| K-7-4 | K-7-3 | 0.657 | 0.600 | 0.772 |
| K-7-2 | K-6-5 | 0.655 | 0.587 | 0.713 |
| K | K-6-4 | 0.639 | 0.633 | 0.938 |
| K-6-3 | K-6-2 | 0.638 | 0.615 | 0.882 |
| K-5-4 | K | 0.640 | 0.599 | 0.816 |
| K-5-3 | K-5-2 | 0.641 | 0.585 | 0.747 |
| K-4-3 | K-4-2 | 0.624 | 0.612 | 0.927 |
| K-3-2 | Q-J-10 | 0.622 | 0.595 | 0.870 |
| Q-J-9 | Q-J-8 | 0.624 | 0.582 | 0.804 |
| Q-J-7 | Q-J-6 | 0.605 | 0.594 | 0.838 |
| Q-J-5 | Q-J-4 | 0.605 | 0.580 | 0.783 |
| Q-J-3 | Q-J-2 | 0.590 | 0.579 | 0.751 |
| Q-10-9 | Q-10-8 | 0.930 | 0.808 | 1.084 |
| Q-10-7 | Q-10-6 | 0.946 | 0.729 | 1.014 |
| Q-10-5 | 7 | 0.964 | 0.660 | 0.951 |
| Q-10-4 | 6 | 0.981 | 0.606 | 0.893 |
| Q-10-3 | 5 | 0.979 | 0.594 | 0.827 |
| Q-10-2 | 4 | 0.979 | 0.572 | 0.811 |
| Q-9-8 | 3 | 0.975 | 0.554 | 0.795 |
| Q-9-7 | 2 | 0.972 | 0.541 | 0.782 |
| Q-9-6 | Q-9-5 | 0.803 | 0.729 | 1.012 |
| Q-9-4 | Q-9-3 | 0.818 | 0.658 | 0.966 |
| Q-9-2 | Q-8-7 | 0.834 | 0.603 | 0.911 |
| Q | Q-8-6 | 0.833 | 0.592 | 0.838 |
| Q-8-5 | 4 | 0.835 | 0.575 | 0.773 |
| Q-8-4 | 3 | 0.833 | 0.556 | 0.760 |
| Q-8-3 | 2 | 0.831 | 0.541 | 0.748 |
| Q-8-2 | Q-7-6 | 0.727 | 0.657 | 0.986 |
| Q | Q-7-5 | 0.743 | 0.602 | 0.948 |
| Q | Q-7-4 | 0.743 | 0.591 | 0.875 |
| Q-7-3 | Q-7-2 | 0.743 | 0.575 | 0.803 |
| Q-6-5 | 3 | 0.742 | 0.558 | 0.738 |
| Q | 2 | 0.743 | 0.544 | 0.731 |
| Q-6-4 | Q | 0.660 | 0.600 | 0.972 |
| Q-6-3 | Q-6-2 | 0.657 | 0.587 | 0.916 |
| Q-5-4 | Q | 0.659 | 0.571 | 0.843 |
| Q-5-3 | Q | 0.660 | 0.558 | 0.770 |
| Q-5-2 | Q-4-3 | 0.660 | 0.545 | 0.711 |
| Q | Q-4-2 | 0.588 | 0.584 | 0.946 |
| Q-3-2 | J-10-9 | 0.590 | 0.569 | 0.887 |
| J-10-8 | J-10-7 | 0.592 | 0.554 | 0.817 |
| J-10-6 | J-10-5 | 0.594 | 0.542 | 0.747 |
| J-10-4 | J-10-3 | 0.577 | 0.567 | 0.924 |
| J-10-2 | J-9-8 | 0.579 | 0.553 | 0.871 |
| J-9-7 | J-9-6 | 0.579 | 0.540 | 0.803 |
| J-9-5 | J-9-4 | 0.561 | 0.551 | 0.838 |
| J-9-3 | J-9-2 | 0.562 | 0.540 | 0.783 |
| J-8-7 | J | 0.545 | 0.538 | 0.752 |
| J-8-6 | 10 | 0.812 | 0.739 | 0.994 |
| J-8-5 | 10 | 0.826 | 0.671 | 0.948 |
| J-8-4 | 10 | 0.843 | 0.611 | 0.894 |
| J-8-3 | 5 | 0.861 | 0.559 | 0.842 |
| J-8-2 | 4 | 0.859 | 0.544 | 0.770 |
| J-7-6 | 3 | 0.859 | 0.528 | 0.757 |
| J | 2 | 0.857 | 0.513 | 0.748 |
| J-7-5 | 10 | 0.740 | 0.671 | 0.969 |
| J | 10 | 0.756 | 0.610 | 0.934 |
| J-7-4 | 10 | 0.772 | 0.557 | 0.879 |
| J-7-3 | 10 | 0.772 | 0.543 | 0.798 |
| J-7-2 | 3 | 0.773 | 0.531 | 0.737 |
| J-6-5 | 2 | 0.772 | 0.515 | 0.729 |
| J | 10 | 0.675 | 0.608 | 0.959 |
| J-6-4 | 10 | 0.689 | 0.555 | 0.920 |
| J | 10 | 0.690 | 0.543 | 0.844 |
| J-6-3 | 10 | 0.692 | 0.529 | 0.767 |
| J-6-2 | 10 | 0.690 | 0.517 | 0.709 |
| J-5-4 | 10 | 0.612 | 0.554 | 0.952 |
| J | 10 | 0.611 | 0.540 | 0.884 |
| J-5-3 | 10 | 0.615 | 0.528 | 0.818 |
| J | 10 | 0.616 | 0.517 | 0.747 |
| J-5-2 | 10 | 0.546 | 0.538 | 0.932 |
| J-4-3 | 10 | 0.548 | 0.525 | 0.873 |
| J | 10 | 0.549 | 0.515 | 0.804 |
| J-4-2 | 10 | 0.533 | 0.524 | 0.837 |
| J-3-2 | 10 | 0.533 | 0.513 | 0.785 |
| 10-9-8 | 10 | 0.521 | 0.513 | 0.753 |
| 10-9-7 | 9 | 0.719 | 0.674 | 0.952 |
| 10-9-6 | 9 | 0.731 | 0.617 | 0.914 |
| 10-9-5 | 9 | 0.751 | 0.559 | 0.863 |
| 10-9-4 | 9 | 0.768 | 0.504 | 0.805 |
| 10-9-3 | 3 | 0.765 | 0.495 | 0.734 |
| 10-9-2 | 2 | 0.763 | 0.480 | 0.726 |
| 10-8-7 | 9 | 0.674 | 0.614 | 0.941 |
| 10-8-6 | 9 | 0.691 | 0.558 | 0.904 |
| 10-8-5 | 9 | 0.711 | 0.503 | 0.847 |
| 10-8-4 | 9 | 0.711 | 0.493 | 0.765 |
| 10-8-3 | 2 | 0.709 | 0.484 | 0.708 |
| 10-8-2 | 9 | 0.620 | 0.557 | 0.935 |
| 10-7-6 | 9 | 0.636 | 0.501 | 0.891 |
| 10-7-5 | 9 | 0.639 | 0.491 | 0.814 |
| 10-7-4 | 9 | 0.639 | 0.480 | 0.743 |
| 10-7-3 | 9 | 0.563 | 0.497 | 0.934 |
| 10-7-2 | 9 | 0.563 | 0.489 | 0.872 |
| 10-6-5 | 9 | 0.566 | 0.480 | 0.802 |
| 10-6-4 | 9 | 0.494 | 0.488 | 0.843 |
| 10-6-3 | 9 | 0.497 | 0.479 | 0.788 |
| 10-6-2 | 9 | 0.487 | 0.480 | 0.753 |
| 10-5-4 | 8 | 0.685 | 0.645 | 0.924 |
| 10-5-3 | 8 | 0.699 | 0.590 | 0.888 |
| 10-5-2 | 8 | 0.717 | 0.526 | 0.829 |
| 10-4-3 | 8 | 0.735 | 0.476 | 0.771 |
| 10-4-2 | 2 | 0.733 | 0.468 | 0.708 |
| 10-3-2 | 8 | 0.648 | 0.585 | 0.919 |
| 9-8-7 | 8 | 0.667 | 0.526 | 0.874 |
| 9-8-6 | 8 | 0.684 | 0.473 | 0.820 |
| 9-8-5 | 8 | 0.684 | 0.467 | 0.741 |
| 9-8-4 | 8 | 0.594 | 0.523 | 0.922 |
| 9-8-3 | 8 | 0.615 | 0.471 | 0.877 |
| 9-8-2 | 8 | 0.613 | 0.466 | 0.800 |
| 9-7-6 | 8 | 0.535 | 0.471 | 0.846 |
| 9-7-5 | 8 | 0.535 | 0.467 | 0.783 |
| 9-7-4 | 8 | 0.470 | 0.467 | 0.761 |
| 9-7-3 | 7 | 0.662 | 0.622 | 0.903 |
| 9-7-2 | 7 | 0.679 | 0.560 | 0.856 |
| 9-6-5 | 7 | 0.696 | 0.500 | 0.804 |
| 9-6-4 | 7 | 0.713 | 0.452 | 0.745 |
| 9-6-3 | 7 | 0.627 | 0.559 | 0.905 |
| 9-6-2 | 7 | 0.646 | 0.498 | 0.860 |
| 9-5-4 | 7 | 0.663 | 0.450 | 0.807 |
| 9-5-3 | 7 | 0.570 | 0.498 | 0.833 |
| 9-5-2 | 7 | 0.591 | 0.453 | 0.790 |
| 9-4-3 | 7 | 0.512 | 0.452 | 0.765 |
| 9-4-2 | 6 | 0.646 | 0.594 | 0.884 |
| 9-3-2 | 6 | 0.664 | 0.538 | 0.844 |
| 8-7-6 | 6 | 0.681 | 0.480 | 0.787 |
| 8-7-5 | 6 | 0.605 | 0.538 | 0.814 |
| 8-7-4 | 6 | 0.625 | 0.481 | 0.771 |
| 8-7-3 | 6 | 0.556 | 0.483 | 0.747 |
| 8-7-2 | 5 | 0.638 | 0.584 | 0.793 |
| 8-6-5 | 5 | 0.654 | 0.529 | 0.752 |
| 8-6-4 | 5 | 0.599 | 0.532 | 0.728 |
| 8-6-3 | 4 | 0.566 | 0.517 | 0.726 |
Three Singletons — Flanking Suited Cards
This table reveals the expected returns for the three possible plays when you are dealt three singletons, particularly when the lowest and highest ones are suited. In 74.1% of cases, the best choice is to keep the suited cards while discarding the middle one. The following table showcases the expected returns for the various ways to choose two out of the three cards.
Three Singletons — Flanking Suited Cards
| 8-6-2 | 8-5-4 | 8-5-3 8-5-2 8-4-3 |
8-4-2 8-3-2 7-6-5 |
7-6-4 7-6-3 7-6-2 |
|---|---|---|---|---|
| 7-5-4 | 7-5-3 | 1.400 | 1.533 | 1.256 |
| 7-5-2 | 7-4-3 | 1.405 | 1.417 | 1.146 |
| 7-4-2 | 10 | 1.404 | 1.332 | 1.065 |
| 7-3-2 | 9 | 1.419 | 1.196 | 0.918 |
| 6-5-4 | 8 | 1.415 | 1.147 | 0.810 |
| 6-5-3 | 7 | 1.418 | 1.109 | 0.778 |
| 6-5-2 | 6 | 1.416 | 1.080 | 0.749 |
| 6-4-3 | 5 | 1.417 | 1.119 | 0.729 |
| 6-4-2 | 4 | 1.413 | 1.098 | 0.706 |
| 6-3-2 | 3 | 1.405 | 1.078 | 0.686 |
| 5-4-3 | 2 | 1.397 | 1.045 | 0.666 |
| 5-4-2 | 5-3-2 | 1.244 | 1.416 | 1.088 |
| 4-3-2 | Hand | 1.250 | 1.329 | 1.021 |
| Discard | 9 | 1.263 | 1.194 | 0.885 |
| Expected | 8 | 1.260 | 1.144 | 0.778 |
| Return | 7 | 1.260 | 1.111 | 0.696 |
| Middle and High | 6 | 1.260 | 1.078 | 0.678 |
| Expected | 5 | 1.263 | 1.124 | 0.660 |
| Return | 4 | 1.260 | 1.103 | 0.641 |
| Low and High | 3 | 1.253 | 1.081 | 0.620 |
| Expected | 2 | 1.248 | 1.048 | 0.605 |
| Return | Low and Middle | 1.133 | 1.331 | 1.011 |
| A-K-Q | A | 1.147 | 1.195 | 0.884 |
| A-K-J | J | 1.145 | 1.147 | 0.780 |
| A-K-10 | 7 | 1.144 | 1.112 | 0.694 |
| A-K-9 | 6 | 1.144 | 1.084 | 0.623 |
| A-K-8 | 5 | 1.146 | 1.125 | 0.606 |
| A-K-7 | 4 | 1.144 | 1.103 | 0.587 |
| A-K-6 | 3 | 1.139 | 1.082 | 0.572 |
| A-K-5 | 2 | 1.134 | 1.050 | 0.557 |
| A-K-4 | 10 | 1.055 | 1.194 | 0.899 |
| A-K-3 | 10 | 1.057 | 1.149 | 0.802 |
| A-K-2 | 10 | 1.054 | 1.109 | 0.718 |
| A-Q-J | 10 | 1.059 | 1.083 | 0.641 |
| A | 10 | 1.063 | 1.131 | 0.572 |
| A-Q-10 | 10 | 1.057 | 1.102 | 0.554 |
| A-Q-9 | 10 | 1.055 | 1.081 | 0.541 |
| A-Q-8 | 10 | 1.048 | 1.049 | 0.525 |
| A-Q-7 | 9 | 0.891 | 1.138 | 0.799 |
| A-Q-6 | 9 | 0.892 | 1.103 | 0.737 |
| A-Q-5 | 9 | 0.894 | 1.076 | 0.663 |
| A-Q-4 | 9 | 0.900 | 1.124 | 0.590 |
| A-Q-3 | 9 | 0.895 | 1.104 | 0.518 |
| A-Q-2 | 9 | 0.891 | 1.075 | 0.504 |
| A-J-10 | 9 | 0.890 | 1.046 | 0.495 |
| A | 8 | 0.839 | 1.102 | 0.751 |
| A-J-9 | 8 | 0.842 | 1.075 | 0.702 |
| A-J-8 | 8 | 0.843 | 1.119 | 0.630 |
| A-J-7 | 8 | 0.844 | 1.101 | 0.550 |
| A-J-6 | 8 | 0.844 | 1.083 | 0.485 |
| A-J-5 | 8 | 0.839 | 1.048 | 0.475 |
| A-J-4 | 7 | 0.802 | 1.070 | 0.726 |
| A-J-3 | 7 | 0.805 | 1.117 | 0.673 |
| A-J-2 | 7 | 0.807 | 1.099 | 0.600 |
| A-10-9 | 7 | 0.806 | 1.081 | 0.520 |
| A | 7 | 0.805 | 1.054 | 0.461 |
| A-10-8 | 6 | 0.775 | 1.120 | 0.707 |
| A-10-7 | 6 | 0.774 | 1.102 | 0.649 |
| A-10-6 | 6 | 0.773 | 1.080 | 0.578 |
| A-10-5 | 6 | 0.773 | 1.055 | 0.502 |
| A-10-4 | 5 | 0.805 | 1.078 | 0.678 |
| A-10-3 | 5 | 0.807 | 1.061 | 0.622 |
| A-10-2 | 5 | 0.805 | 1.034 | 0.553 |
| A-9-8 | 4 | 0.782 | 1.059 | 0.588 |
| A | 4 | 0.782 | 1.033 | 0.533 |
| A-9-7 | 3 | 0.760 | 1.030 | 0.504 |
| A | A-9-6 | 1.144 | 1.318 | 1.073 |
| A-9-5 | A-9-4 | 1.147 | 1.249 | 1.006 |
| A-9-3 | 9 | 1.162 | 1.116 | 0.867 |
| A-9-2 | 8 | 1.175 | 1.038 | 0.783 |
| A-8-7 | 7 | 1.171 | 1.009 | 0.694 |
| A | 6 | 1.173 | 0.985 | 0.679 |
| A-8-6 | 5 | 1.172 | 0.969 | 0.661 |
| A | 4 | 1.172 | 0.951 | 0.643 |
| A-8-5 | 3 | 1.166 | 0.935 | 0.623 |
| A | 2 | 1.159 | 0.914 | 0.607 |
| A-8-4 | A-8-3 | 1.047 | 1.246 | 0.994 |
| A-8-2 | A-7-6 | 1.063 | 1.115 | 0.865 |
| A | 8 | 1.078 | 1.037 | 0.783 |
| A-7-5 | 7 | 1.075 | 1.008 | 0.691 |
| A | 6 | 1.076 | 0.991 | 0.622 |
| A-7-4 | 5 | 1.078 | 0.973 | 0.608 |
| A | 4 | 1.073 | 0.952 | 0.589 |
| A-7-3 | 3 | 1.069 | 0.935 | 0.571 |
| A-7-2 | 2 | 1.061 | 0.914 | 0.556 |
| A-6-5 | 10 | 0.988 | 1.112 | 0.882 |
| A | 10 | 1.002 | 1.035 | 0.808 |
| A-6-4 | 10 | 1.003 | 1.008 | 0.715 |
| A | 6 | 1.005 | 0.991 | 0.638 |
| A-6-3 | 5 | 1.005 | 0.977 | 0.574 |
| A | 4 | 1.003 | 0.952 | 0.557 |
| A-6-2 | 3 | 0.998 | 0.934 | 0.541 |
| A-5-4 | 2 | 0.994 | 0.917 | 0.527 |
| A | 9 | 0.838 | 1.032 | 0.805 |
| A-5-3 | 9 | 0.838 | 1.005 | 0.737 |
| A | 9 | 0.841 | 0.986 | 0.664 |
| A-5-2 | 9 | 0.842 | 0.974 | 0.591 |
| A-4-3 | 9 | 0.841 | 0.954 | 0.522 |
| A | 9 | 0.838 | 0.933 | 0.508 |
| A-4-2 | 9 | 0.831 | 0.913 | 0.496 |
| A-3-2 | 8 | 0.743 | 1.001 | 0.763 |
| K-Q-J | 8 | 0.742 | 0.981 | 0.705 |
| K | 8 | 0.744 | 0.968 | 0.635 |
| K-Q-10 | 8 | 0.745 | 0.949 | 0.556 |
| K | 8 | 0.745 | 0.937 | 0.491 |
| K-Q-9 | 8 | 0.741 | 0.912 | 0.481 |
| K-Q-8 | 7 | 0.714 | 0.983 | 0.729 |
| K-Q-7 | 7 | 0.714 | 0.964 | 0.677 |
| K-Q-6 | 7 | 0.715 | 0.950 | 0.603 |
| K-Q-5 | 7 | 0.716 | 0.933 | 0.526 |
| K-Q-4 | 7 | 0.714 | 0.917 | 0.463 |
| K-Q-3 | 6 | 0.690 | 0.964 | 0.709 |
| K-Q-2 | 6 | 0.692 | 0.947 | 0.650 |
| K-J-10 | 6 | 0.692 | 0.928 | 0.580 |
| K | 6 | 0.693 | 0.913 | 0.505 |
| K-J-9 | 5 | 0.670 | 0.942 | 0.695 |
| K | 5 | 0.672 | 0.927 | 0.641 |
| K-J-8 | 5 | 0.672 | 0.909 | 0.570 |
| K-J-7 | 4 | 0.653 | 0.926 | 0.609 |
| K-J-6 | 4 | 0.652 | 0.908 | 0.553 |
| K-J-5 | 3 | 0.632 | 0.906 | 0.524 |
| K-J-4 | K-J-3 | 0.991 | 1.193 | 0.974 |
| K-J-2 | K-10-9 | 1.009 | 1.069 | 0.849 |
| K | 8 | 1.023 | 0.993 | 0.766 |
| K-10-8 | 7 | 1.038 | 0.933 | 0.697 |
| K | 6 | 1.037 | 0.920 | 0.622 |
| K-10-7 | 5 | 1.037 | 0.902 | 0.607 |
| K-10-6 | 4 | 1.036 | 0.885 | 0.589 |
| K-10-5 | 3 | 1.035 | 0.872 | 0.572 |
| K-10-4 | 2 | 1.026 | 0.851 | 0.555 |
| K-10-3 | 10 | 0.945 | 1.067 | 0.865 |
| K-10-2 | 10 | 0.965 | 0.991 | 0.792 |
| K-9-8 | 7 | 0.978 | 0.933 | 0.721 |
| K | 6 | 0.976 | 0.920 | 0.637 |
| K-9-7 | 5 | 0.977 | 0.904 | 0.572 |
| K | 4 | 0.976 | 0.884 | 0.554 |
| K-9-6 | 3 | 0.975 | 0.868 | 0.540 |
| K | 2 | 0.971 | 0.854 | 0.527 |
| K-9-5 | 9 | 0.807 | 0.989 | 0.790 |
| K-9-4 | 9 | 0.821 | 0.929 | 0.742 |
| K-9-3 | 9 | 0.820 | 0.915 | 0.662 |
| K-9-2 | 9 | 0.820 | 0.903 | 0.587 |
| K-8-7 | 9 | 0.821 | 0.888 | 0.518 |
| K | 9 | 0.824 | 0.870 | 0.509 |
| K-8-6 | 9 | 0.817 | 0.852 | 0.494 |
| K | 8 | 0.723 | 0.925 | 0.766 |
| K-8-5 | 8 | 0.724 | 0.912 | 0.704 |
| K | 8 | 0.724 | 0.901 | 0.633 |
| K-8-4 | 8 | 0.726 | 0.884 | 0.555 |
| K | 8 | 0.726 | 0.869 | 0.490 |
| K-8-3 | 8 | 0.725 | 0.853 | 0.482 |
| K-8-2 | 7 | 0.645 | 0.910 | 0.736 |
| K-7-6 | 7 | 0.646 | 0.897 | 0.681 |
| K | 7 | 0.647 | 0.884 | 0.604 |
| K-7-5 | 7 | 0.649 | 0.868 | 0.528 |
| K | 7 | 0.647 | 0.854 | 0.465 |
| K-7-4 | 6 | 0.630 | 0.898 | 0.710 |
| K | 6 | 0.629 | 0.880 | 0.650 |
| K-7-3 | 6 | 0.631 | 0.865 | 0.581 |
| K | 6 | 0.634 | 0.853 | 0.505 |
| K-7-2 | 5 | 0.613 | 0.877 | 0.697 |
| K-6-5 | 5 | 0.613 | 0.863 | 0.642 |
| K | 5 | 0.614 | 0.850 | 0.571 |
| K-6-4 | 4 | 0.596 | 0.863 | 0.610 |
| K | 4 | 0.595 | 0.848 | 0.554 |
| K-6-3 | 3 | 0.580 | 0.847 | 0.525 |
| K | 10 | 0.930 | 1.051 | 0.850 |
| K-6-2 | 10 | 0.946 | 0.977 | 0.774 |
| K | 7 | 0.964 | 0.915 | 0.707 |
| K-5-4 | 6 | 0.979 | 0.863 | 0.643 |
| K | 5 | 0.980 | 0.853 | 0.571 |
| K-5-3 | 4 | 0.978 | 0.834 | 0.555 |
| K | 3 | 0.975 | 0.817 | 0.539 |
| K-5-2 | 2 | 0.972 | 0.804 | 0.526 |
| K | 9 | 0.797 | 0.976 | 0.772 |
| K-4-3 | 9 | 0.814 | 0.913 | 0.725 |
| K | 9 | 0.831 | 0.863 | 0.669 |
| K-4-2 | 9 | 0.831 | 0.851 | 0.587 |
| K | 9 | 0.832 | 0.835 | 0.518 |
| K-3-2 | 3 | 0.828 | 0.819 | 0.505 |
| K | 2 | 0.827 | 0.804 | 0.493 |
| Q-J-10 | 8 | 0.721 | 0.910 | 0.750 |
| Q | 8 | 0.738 | 0.860 | 0.713 |
| Q-J-9 | 8 | 0.737 | 0.847 | 0.633 |
| Q | 8 | 0.739 | 0.836 | 0.554 |
| Q-J-8 | 8 | 0.740 | 0.819 | 0.488 |
| Q-J-7 | 8 | 0.739 | 0.808 | 0.479 |
| Q-J-6 | 7 | 0.653 | 0.858 | 0.742 |
| Q-J-5 | 7 | 0.652 | 0.847 | 0.680 |
| Q-J-4 | 7 | 0.653 | 0.833 | 0.604 |
| Q-J-3 | 7 | 0.655 | 0.819 | 0.528 |
| Q-J-2 | 7 | 0.654 | 0.808 | 0.466 |
| Q-10-9 | 6 | 0.583 | 0.845 | 0.716 |
| Q | 6 | 0.585 | 0.830 | 0.656 |
| Q-10-8 | 6 | 0.587 | 0.819 | 0.584 |
| Q | 6 | 0.586 | 0.807 | 0.507 |
| Q-10-7 | 5 | 0.571 | 0.829 | 0.698 |
| Q-10-6 | 5 | 0.572 | 0.816 | 0.641 |
| Q-10-5 | 5 | 0.573 | 0.803 | 0.571 |
| Q-10-4 | 4 | 0.553 | 0.815 | 0.609 |
| Q-10-3 | 4 | 0.554 | 0.803 | 0.554 |
| Q-10-2 | 3 | 0.538 | 0.801 | 0.524 |
| Q-9-8 | 9 | 0.810 | 0.981 | 0.756 |
| Q | 9 | 0.824 | 0.916 | 0.706 |
| Q-9-7 | 9 | 0.842 | 0.861 | 0.649 |
| Q | 5 | 0.859 | 0.815 | 0.592 |
| Q-9-6 | 4 | 0.856 | 0.802 | 0.515 |
| Q | 3 | 0.858 | 0.785 | 0.504 |
| Q-9-5 | 2 | 0.854 | 0.773 | 0.491 |
| Q | 8 | 0.737 | 0.918 | 0.732 |
| Q-9-4 | 8 | 0.752 | 0.860 | 0.694 |
| Q-9-3 | 8 | 0.770 | 0.815 | 0.639 |
| Q-9-2 | 8 | 0.769 | 0.801 | 0.553 |
| Q-8-7 | 8 | 0.770 | 0.788 | 0.485 |
| Q | 8 | 0.769 | 0.773 | 0.477 |
| Q-8-6 | 7 | 0.670 | 0.859 | 0.727 |
| Q | 7 | 0.686 | 0.811 | 0.683 |
| Q-8-5 | 7 | 0.687 | 0.800 | 0.602 |
| Q | 7 | 0.688 | 0.790 | 0.525 |
| Q-8-4 | 7 | 0.688 | 0.777 | 0.465 |
| Q | 6 | 0.609 | 0.813 | 0.722 |
| Q-8-3 | 6 | 0.608 | 0.801 | 0.653 |
| Q | 6 | 0.609 | 0.787 | 0.581 |
| Q-8-2 | 6 | 0.611 | 0.776 | 0.508 |
| Q | 5 | 0.541 | 0.795 | 0.705 |
| Q-7-6 | 5 | 0.543 | 0.783 | 0.645 |
| Q | 5 | 0.545 | 0.773 | 0.575 |
| Q-7-5 | 4 | 0.528 | 0.783 | 0.609 |
| Q | 4 | 0.530 | 0.773 | 0.555 |
| Q-7-4 | 3 | 0.516 | 0.774 | 0.525 |
| Q | 8 | 0.717 | 0.918 | 0.715 |
| Q-7-3 | 8 | 0.732 | 0.864 | 0.674 |
| Q | 8 | 0.748 | 0.810 | 0.619 |
| Q-7-2 | 4 | 0.765 | 0.759 | 0.556 |
| Q | 3 | 0.763 | 0.751 | 0.484 |
| Q-6-5 | 2 | 0.764 | 0.736 | 0.476 |
| Q | 7 | 0.674 | 0.862 | 0.707 |
| Q-6-4 | 7 | 0.690 | 0.808 | 0.666 |
| Q | 7 | 0.707 | 0.759 | 0.607 |
| Q-6-3 | 7 | 0.708 | 0.749 | 0.523 |
| Q | 7 | 0.706 | 0.737 | 0.462 |
| Q-6-2 | 6 | 0.618 | 0.808 | 0.706 |
| Q | 6 | 0.635 | 0.756 | 0.657 |
| Q-5-4 | 6 | 0.636 | 0.748 | 0.578 |
| Q | 6 | 0.637 | 0.738 | 0.504 |
| Q-5-3 | 5 | 0.562 | 0.756 | 0.710 |
| Q | 5 | 0.560 | 0.749 | 0.642 |
| Q-5-2 | 5 | 0.562 | 0.735 | 0.572 |
| Q | 4 | 0.491 | 0.746 | 0.616 |
| Q-4-3 | 4 | 0.494 | 0.738 | 0.557 |
| Q | 3 | 0.482 | 0.738 | 0.524 |
| Q-4-2 | 7 | 0.685 | 0.886 | 0.688 |
| Q | 7 | 0.700 | 0.835 | 0.648 |
| Q-3-2 | 7 | 0.717 | 0.777 | 0.588 |
| Q | 3 | 0.736 | 0.728 | 0.530 |
| J-10-9 | 2 | 0.735 | 0.722 | 0.463 |
| J | 6 | 0.649 | 0.834 | 0.687 |
| J-10-8 | 6 | 0.666 | 0.775 | 0.640 |
| J | 6 | 0.682 | 0.725 | 0.584 |
| J-10-7 | 6 | 0.682 | 0.719 | 0.501 |
| J-10-6 | 5 | 0.593 | 0.772 | 0.692 |
| J-10-5 | 5 | 0.611 | 0.724 | 0.648 |
| J-10-4 | 5 | 0.612 | 0.717 | 0.570 |
| J-10-3 | 4 | 0.534 | 0.727 | 0.619 |
| J-10-2 | 4 | 0.532 | 0.719 | 0.557 |
| J-9-8 | 3 | 0.468 | 0.719 | 0.531 |
| J | 6 | 0.662 | 0.860 | 0.669 |
| J-9-7 | 6 | 0.679 | 0.803 | 0.621 |
| J | 6 | 0.698 | 0.745 | 0.567 |
| J-9-6 | 2 | 0.712 | 0.700 | 0.505 |
| J | 5 | 0.626 | 0.800 | 0.675 |
| J-9-5 | 5 | 0.646 | 0.742 | 0.631 |
| J | 5 | 0.663 | 0.697 | 0.576 |
| J-9-4 | 4 | 0.571 | 0.746 | 0.603 |
| J-9-3 | 4 | 0.589 | 0.699 | 0.561 |
| J-9-2 | 3 | 0.510 | 0.701 | 0.536 |
| J-8-7 | 5 | 0.645 | 0.829 | 0.656 |
| J | 5 | 0.662 | 0.776 | 0.612 |
| J-8-6 | 5 | 0.681 | 0.721 | 0.557 |
| J | 4 | 0.605 | 0.778 | 0.587 |
| J-8-5 | 4 | 0.623 | 0.722 | 0.543 |
| J | 3 | 0.553 | 0.723 | 0.518 |
| J-8-4 | 4 | 0.635 | 0.816 | 0.562 |
| J | 4 | 0.654 | 0.762 | 0.519 |
| J-8-3 | 3 | 0.597 | 0.764 | 0.495 |
| J-8-2 | 3 | 0.567 | 0.748 | 0.494 |
Three Singletons — Two Highest Cards of the Same Suit
The subsequent table demonstrates the expected returns for all three potential actions when you hold three singletons, given that the lowest two are suited. In every instance, it is optimal to maintain the suited cards and dispose of the lowest. The remaining situation involves discarding the lowest card. The following table illustrates the expected return for all three selections among the three cards.
Three Singletons — Two Highest Cards of the Same Suit
| J-7-6 | J | J-7-5 J J-7-4 |
J J-7-3 J |
J-7-2 J J-6-5 |
|---|---|---|---|---|
| J | J-6-4 | 1.632 | 1.286 | 1.252 |
| J | J-6-3 | 1.638 | 1.162 | 1.143 |
| J | 10 | 1.638 | 1.066 | 1.060 |
| J-6-2 | 9 | 1.651 | 0.920 | 0.912 |
| J | 8 | 1.646 | 0.865 | 0.803 |
| J-5-4 | 7 | 1.651 | 0.823 | 0.769 |
| J | 6 | 1.645 | 0.789 | 0.743 |
| J-5-3 | 5 | 1.652 | 0.837 | 0.720 |
| J | 4 | 1.646 | 0.810 | 0.699 |
| J-5-2 | 3 | 1.636 | 0.784 | 0.678 |
| J | 2 | 1.629 | 0.752 | 0.657 |
| J-4-3 | J | 1.493 | 1.160 | 1.088 |
| J-4-2 | 10 | 1.498 | 1.067 | 1.019 |
| J | 9 | 1.512 | 0.921 | 0.881 |
| J-3-2 | 8 | 1.506 | 0.865 | 0.773 |
| J | 7 | 1.506 | 0.827 | 0.691 |
| 10-9-8 | 6 | 1.506 | 0.791 | 0.674 |
| 10-9-7 | 5 | 1.510 | 0.837 | 0.654 |
| 10-9-6 | 4 | 1.507 | 0.812 | 0.633 |
| 10-9-5 | 3 | 1.499 | 0.786 | 0.613 |
| 10-9-4 | 2 | 1.491 | 0.753 | 0.597 |
| 10-9-3 | 10 | 1.387 | 1.066 | 1.009 |
| 10-9-2 | 9 | 1.402 | 0.919 | 0.882 |
| 10-8-7 | 8 | 1.400 | 0.864 | 0.777 |
| 10-8-6 | 7 | 1.401 | 0.827 | 0.689 |
| 10-8-5 | 6 | 1.399 | 0.796 | 0.617 |
| 10-8-4 | 5 | 1.404 | 0.839 | 0.603 |
| 10-8-3 | 4 | 1.401 | 0.813 | 0.585 |
| 10-8-2 | 3 | 1.395 | 0.790 | 0.567 |
| 10-7-6 | 2 | 1.388 | 0.754 | 0.550 |
| 10-7-5 | 9 | 1.321 | 0.920 | 0.900 |
| 10-7-4 | 8 | 1.321 | 0.865 | 0.799 |
| 10-7-3 | 7 | 1.320 | 0.826 | 0.716 |
| 10-7-2 | 6 | 1.322 | 0.795 | 0.635 |
| 10-6-5 | 5 | 1.326 | 0.842 | 0.570 |
| 10-6-4 | 4 | 1.324 | 0.816 | 0.552 |
| 10-6-3 | 3 | 1.318 | 0.791 | 0.536 |
| 10-6-2 | 2 | 1.315 | 0.757 | 0.523 |
| 10-5-4 | 8 | 1.168 | 0.856 | 0.799 |
| 10-5-3 | 7 | 1.171 | 0.819 | 0.736 |
| 10-5-2 | 6 | 1.170 | 0.787 | 0.660 |
| 10-4-3 | 5 | 1.174 | 0.835 | 0.584 |
| 10-4-2 | 4 | 1.174 | 0.815 | 0.517 |
| 10-3-2 | 3 | 1.170 | 0.786 | 0.505 |
| 9-8-7 | 2 | 1.164 | 0.752 | 0.489 |
| 9-8-6 | 7 | 1.123 | 0.816 | 0.753 |
| 9-8-5 | 6 | 1.122 | 0.786 | 0.700 |
| 9-8-4 | 5 | 1.126 | 0.835 | 0.628 |
| 9-8-3 | 4 | 1.127 | 0.812 | 0.549 |
| 9-8-2 | 3 | 1.123 | 0.791 | 0.483 |
| 9-7-6 | 2 | 1.118 | 0.752 | 0.474 |
| 9-7-5 | 6 | 1.087 | 0.783 | 0.726 |
| 9-7-4 | 5 | 1.091 | 0.831 | 0.672 |
| 9-7-3 | 4 | 1.091 | 0.809 | 0.599 |
| 9-7-2 | 3 | 1.090 | 0.788 | 0.520 |
| 9-6-5 | 2 | 1.088 | 0.758 | 0.458 |
| 9-6-4 | 5 | 1.063 | 0.834 | 0.707 |
| 9-6-3 | 4 | 1.064 | 0.812 | 0.649 |
| 9-6-2 | 3 | 1.063 | 0.789 | 0.576 |
| 9-5-4 | 2 | 1.062 | 0.761 | 0.502 |
| 9-5-3 | 4 | 1.090 | 0.789 | 0.677 |
| 9-5-2 | 3 | 1.094 | 0.771 | 0.622 |
| 9-4-3 | 2 | 1.091 | 0.738 | 0.552 |
| 9-4-2 | 3 | 1.072 | 0.768 | 0.589 |
| 9-3-2 | 2 | 1.069 | 0.735 | 0.532 |
| 8-7-6 | 2 | 1.050 | 0.736 | 0.504 |
| 8-7-5 | 8-7-4 | 1.384 | 1.072 | 1.071 |
| 8-7-3 | 10 | 1.387 | 0.995 | 1.002 |
| 8-7-2 | 9 | 1.398 | 0.849 | 0.862 |
| 8-6-5 | 8 | 1.414 | 0.764 | 0.779 |
| 8-6-4 | 7 | 1.412 | 0.733 | 0.689 |
| 8-6-3 | 6 | 1.414 | 0.709 | 0.672 |
| 8-6-2 | 5 | 1.411 | 0.689 | 0.655 |
| 8-5-4 | 4 | 1.408 | 0.668 | 0.635 |
| 8-5-3 | 3 | 1.402 | 0.647 | 0.617 |
| 8-5-2 | 2 | 1.393 | 0.625 | 0.599 |
| 8-4-3 | 10 | 1.291 | 0.992 | 0.991 |
| 8-4-2 | 9 | 1.311 | 0.849 | 0.864 |
| 8-3-2 | 8 | 1.323 | 0.765 | 0.783 |
| 7-6-5 | 7 | 1.323 | 0.735 | 0.688 |
| 7-6-4 | 6 | 1.321 | 0.712 | 0.619 |
| 7-6-3 | 5 | 1.322 | 0.689 | 0.604 |
| 7-6-2 | 4 | 1.322 | 0.669 | 0.587 |
| 7-5-4 | 3 | 1.316 | 0.649 | 0.569 |
| 7-5-3 | 2 | 1.309 | 0.629 | 0.552 |
| 7-5-2 | 9 | 1.242 | 0.850 | 0.885 |
| 7-4-3 | 8 | 1.258 | 0.762 | 0.806 |
| 7-4-2 | 7 | 1.258 | 0.734 | 0.714 |
| 7-3-2 | 6 | 1.258 | 0.713 | 0.637 |
| 6-5-4 | 5 | 1.254 | 0.691 | 0.570 |
| 6-5-3 | 4 | 1.254 | 0.670 | 0.553 |
| 6-5-2 | 3 | 1.252 | 0.649 | 0.538 |
| 6-4-3 | 2 | 1.246 | 0.629 | 0.522 |
| 6-4-2 | 8 | 1.104 | 0.758 | 0.805 |
| 6-3-2 | 7 | 1.104 | 0.730 | 0.736 |
| 5-4-3 | 6 | 1.106 | 0.707 | 0.662 |
| 5-4-2 | 5 | 1.107 | 0.688 | 0.586 |
| 5-3-2 | 4 | 1.105 | 0.670 | 0.519 |
| 4-3-2 | 3 | 1.103 | 0.647 | 0.504 |
| Hand | 2 | 1.097 | 0.627 | 0.494 |
| Discard | 7 | 1.016 | 0.726 | 0.762 |
| Expected | 6 | 1.016 | 0.701 | 0.706 |
| Return | 5 | 1.019 | 0.686 | 0.633 |
| Middle and High | 4 | 1.019 | 0.666 | 0.555 |
| Expected | 3 | 1.017 | 0.647 | 0.488 |
| Return | 2 | 1.013 | 0.624 | 0.478 |
| Low and High | 6 | 0.992 | 0.702 | 0.727 |
| Expected | 5 | 0.993 | 0.685 | 0.679 |
| Return | 4 | 0.992 | 0.664 | 0.601 |
| Low and Middle | 3 | 0.993 | 0.647 | 0.524 |
| A-K-Q | 2 | 0.992 | 0.631 | 0.464 |
| K | 5 | 0.970 | 0.681 | 0.710 |
| A-K-J | 4 | 0.970 | 0.662 | 0.649 |
| K | 3 | 0.970 | 0.643 | 0.577 |
| A-K-10 | 2 | 0.972 | 0.627 | 0.503 |
| A-K-9 | 4 | 0.954 | 0.658 | 0.697 |
| A-K-8 | 3 | 0.951 | 0.641 | 0.642 |
| A-K-7 | 2 | 0.953 | 0.623 | 0.571 |
| A-K-6 | 3 | 0.935 | 0.638 | 0.610 |
| A-K-5 | 2 | 0.934 | 0.621 | 0.553 |
| A-K-4 | 2 | 0.916 | 0.620 | 0.523 |
| A-K-3 | 10 | 1.228 | 0.948 | 0.974 |
| A-K-2 | 9 | 1.245 | 0.814 | 0.846 |
| A-Q-J | 8 | 1.262 | 0.732 | 0.765 |
| Q | 7 | 1.273 | 0.662 | 0.692 |
| A-Q-10 | 6 | 1.274 | 0.648 | 0.618 |
| Q | 5 | 1.275 | 0.628 | 0.602 |
| A-Q-9 | 4 | 1.274 | 0.608 | 0.584 |
| A-Q-8 | 3 | 1.269 | 0.591 | 0.567 |
| A-Q-7 | 2 | 1.265 | 0.573 | 0.550 |
| A-Q-6 | 9 | 1.192 | 0.814 | 0.867 |
| A-Q-5 | 8 | 1.204 | 0.730 | 0.788 |
| A-Q-4 | 7 | 1.224 | 0.665 | 0.720 |
| A-Q-3 | 6 | 1.219 | 0.648 | 0.633 |
| A-Q-2 | 5 | 1.221 | 0.631 | 0.568 |
| A-J-10 | 4 | 1.219 | 0.608 | 0.551 |
| J | 3 | 1.216 | 0.590 | 0.537 |
| A-J-9 | 2 | 1.213 | 0.576 | 0.523 |
| J | 8 | 1.062 | 0.724 | 0.789 |
| A-J-8 | 7 | 1.076 | 0.658 | 0.739 |
| J | 6 | 1.078 | 0.645 | 0.661 |
| A-J-7 | 5 | 1.077 | 0.630 | 0.587 |
| A-J-6 | 4 | 1.078 | 0.611 | 0.517 |
| A-J-5 | 3 | 1.074 | 0.590 | 0.504 |
| A-J-4 | 2 | 1.072 | 0.573 | 0.491 |
| A-J-3 | 7 | 0.986 | 0.655 | 0.766 |
| A-J-2 | 6 | 0.988 | 0.641 | 0.705 |
| A-10-9 | 5 | 0.987 | 0.626 | 0.632 |
| A-10-8 | 4 | 0.991 | 0.610 | 0.555 |
| A-10-7 | 3 | 0.990 | 0.593 | 0.488 |
| A-10-6 | 2 | 0.986 | 0.574 | 0.478 |
| A-10-5 | 6 | 0.916 | 0.639 | 0.736 |
| A-10-4 | 5 | 0.916 | 0.625 | 0.681 |
| A-10-3 | 4 | 0.917 | 0.605 | 0.604 |
| A-10-2 | 3 | 0.916 | 0.589 | 0.526 |
| A-9-8 | 2 | 0.916 | 0.574 | 0.465 |
| A-9-7 | 5 | 0.902 | 0.625 | 0.710 |
| A-9-6 | 4 | 0.902 | 0.604 | 0.651 |
| A-9-5 | 3 | 0.903 | 0.589 | 0.579 |
| A-9-4 | 2 | 0.904 | 0.573 | 0.504 |
| A-9-3 | 4 | 0.887 | 0.599 | 0.698 |
| A-9-2 | 3 | 0.885 | 0.583 | 0.643 |
| A-8-7 | 2 | 0.889 | 0.571 | 0.573 |
| A-8-6 | 3 | 0.872 | 0.584 | 0.608 |
| A-8-5 | 2 | 0.870 | 0.568 | 0.555 |
| A-8-4 | 2 | 0.855 | 0.568 | 0.525 |
| A-8-3 | 9 | 1.165 | 0.803 | 0.850 |
| A-8-2 | 8 | 1.183 | 0.723 | 0.773 |
| A-7-6 | 7 | 1.197 | 0.654 | 0.704 |
| A-7-5 | 6 | 1.214 | 0.599 | 0.641 |
| A-7-4 | 5 | 1.213 | 0.585 | 0.566 |
| A-7-3 | 4 | 1.210 | 0.564 | 0.551 |
| A-7-2 | 3 | 1.209 | 0.547 | 0.535 |
| A-6-5 | 2 | 1.206 | 0.533 | 0.521 |
| A-6-4 | 8 | 1.046 | 0.721 | 0.772 |
| A-6-3 | 7 | 1.062 | 0.650 | 0.725 |
| A-6-2 | 6 | 1.077 | 0.596 | 0.666 |
| A-5-4 | 5 | 1.078 | 0.585 | 0.586 |
| A-5-3 | 4 | 1.075 | 0.566 | 0.516 |
| A-5-2 | 3 | 1.077 | 0.548 | 0.504 |
| A-4-3 | 2 | 1.075 | 0.534 | 0.491 |
| A-4-2 | 7 | 0.976 | 0.650 | 0.753 |
| A-3-2 | 6 | 0.992 | 0.593 | 0.710 |
| K-Q-J | 5 | 0.990 | 0.581 | 0.632 |
| Q | 4 | 0.994 | 0.566 | 0.553 |
| K-Q-10 | 3 | 0.990 | 0.549 | 0.485 |
| Q | 2 | 0.989 | 0.533 | 0.476 |
| K-Q-9 | 6 | 0.914 | 0.591 | 0.740 |
| K-Q-8 | 5 | 0.914 | 0.581 | 0.681 |
| K-Q-7 | 4 | 0.916 | 0.563 | 0.603 |
| K-Q-6 | 3 | 0.915 | 0.548 | 0.526 |
| K-Q-5 | 2 | 0.915 | 0.536 | 0.465 |
| K-Q-4 | 5 | 0.848 | 0.577 | 0.716 |
| K-Q-3 | 4 | 0.851 | 0.562 | 0.655 |
| K-Q-2 | 3 | 0.850 | 0.546 | 0.582 |
| K-J-10 | 2 | 0.853 | 0.534 | 0.507 |
| J | 4 | 0.839 | 0.559 | 0.698 |
| K-J-9 | 3 | 0.839 | 0.541 | 0.641 |
| J | 2 | 0.840 | 0.531 | 0.572 |
| K-J-8 | 3 | 0.822 | 0.542 | 0.609 |
| K-J-7 | 2 | 0.823 | 0.530 | 0.555 |
| K-J-6 | 2 | 0.810 | 0.530 | 0.524 |
| K-J-5 | 8 | 1.050 | 0.735 | 0.756 |
| K-J-4 | 7 | 1.066 | 0.667 | 0.706 |
| K-J-3 | 6 | 1.083 | 0.604 | 0.649 |
| K-J-2 | 5 | 1.099 | 0.553 | 0.592 |
| K-10-9 | 4 | 1.096 | 0.538 | 0.513 |
| K-10-8 | 3 | 1.097 | 0.521 | 0.501 |
| K-10-7 | 2 | 1.093 | 0.508 | 0.488 |
| K-10-6 | 7 | 0.983 | 0.665 | 0.733 |
| K-10-5 | 6 | 0.999 | 0.604 | 0.693 |
| K-10-4 | 5 | 1.016 | 0.553 | 0.638 |
| K-10-3 | 4 | 1.014 | 0.538 | 0.549 |
| K-10-2 | 3 | 1.016 | 0.524 | 0.486 |
| K-9-8 | 2 | 1.014 | 0.507 | 0.474 |
| K-9-7 | 6 | 0.922 | 0.602 | 0.724 |
| K-9-6 | 5 | 0.937 | 0.551 | 0.685 |
| K-9-5 | 4 | 0.937 | 0.536 | 0.599 |
| K-9-4 | 3 | 0.937 | 0.523 | 0.523 |
| K-9-3 | 2 | 0.939 | 0.511 | 0.462 |
| K-9-2 | 5 | 0.866 | 0.549 | 0.721 |
| K-8-7 | 4 | 0.864 | 0.533 | 0.653 |
| K-8-6 | 3 | 0.866 | 0.520 | 0.581 |
| K-8-5 | 2 | 0.868 | 0.510 | 0.505 |
| K-8-4 | 4 | 0.803 | 0.531 | 0.705 |
| K-8-3 | 3 | 0.804 | 0.519 | 0.645 |
| K-8-2 | 2 | 0.807 | 0.508 | 0.575 |
| K-7-6 | 3 | 0.792 | 0.518 | 0.609 |
| K-7-5 | 2 | 0.794 | 0.506 | 0.555 |
| K-7-4 | 2 | 0.779 | 0.506 | 0.525 |
| K-7-3 | 7 | 0.959 | 0.671 | 0.715 |
| K-7-2 | 6 | 0.975 | 0.614 | 0.673 |
| K-6-5 | 5 | 0.990 | 0.556 | 0.619 |
| K-6-4 | 4 | 1.006 | 0.500 | 0.554 |
| K-6-3 | 3 | 1.006 | 0.488 | 0.481 |
| K-6-2 | 2 | 1.003 | 0.474 | 0.471 |
| K-5-4 | 6 | 0.918 | 0.611 | 0.707 |
| K-5-3 | 5 | 0.937 | 0.554 | 0.668 |
| K-5-2 | 4 | 0.951 | 0.497 | 0.605 |
| K-4-3 | 3 | 0.953 | 0.486 | 0.520 |
| K-4-2 | 2 | 0.952 | 0.478 | 0.458 |
| K-3-2 | 5 | 0.869 | 0.553 | 0.704 |
| Q-J-10 | 4 | 0.883 | 0.497 | 0.656 |
| J | 3 | 0.886 | 0.486 | 0.578 |
| Q-J-9 | 2 | 0.887 | 0.475 | 0.503 |
| J | 4 | 0.817 | 0.495 | 0.707 |
| Q-J-8 | 3 | 0.817 | 0.485 | 0.645 |
| Q-J-7 | 2 | 0.818 | 0.472 | 0.571 |
| Q-J-6 | 3 | 0.754 | 0.485 | 0.616 |
| Q-J-5 | 2 | 0.755 | 0.476 | 0.556 |
| Q-J-4 | 2 | 0.744 | 0.476 | 0.524 |
| Q-J-3 | 6 | 0.927 | 0.643 | 0.690 |
| Q-J-2 | 5 | 0.941 | 0.587 | 0.649 |
| Q-10-9 | 4 | 0.957 | 0.525 | 0.589 |
| Q-10-8 | 3 | 0.973 | 0.472 | 0.525 |
| Q-10-7 | 2 | 0.973 | 0.464 | 0.456 |
| Q-10-6 | 5 | 0.892 | 0.587 | 0.688 |
| Q-10-5 | 4 | 0.907 | 0.522 | 0.639 |
| Q-10-4 | 3 | 0.923 | 0.468 | 0.582 |
| Q-10-3 | 2 | 0.925 | 0.463 | 0.502 |
| Q-10-2 | 4 | 0.841 | 0.520 | 0.692 |
| Q-9-8 | 3 | 0.859 | 0.467 | 0.647 |
| Q-9-7 | 2 | 0.860 | 0.462 | 0.569 |
| Q-9-6 | 3 | 0.786 | 0.468 | 0.621 |
| Q-9-5 | 2 | 0.787 | 0.463 | 0.556 |
| Q-9-4 | 2 | 0.724 | 0.463 | 0.531 |
| Q-9-3 | 5 | 0.899 | 0.618 | 0.668 |
| Q-9-2 | 4 | 0.915 | 0.559 | 0.622 |
| Q-8-7 | 3 | 0.933 | 0.498 | 0.565 |
| Q-8-6 | 2 | 0.947 | 0.449 | 0.505 |
| Q-8-5 | 4 | 0.868 | 0.557 | 0.675 |
| Q-8-4 | 3 | 0.885 | 0.493 | 0.630 |
| Q-8-3 | 2 | 0.902 | 0.447 | 0.574 |
| Q-8-2 | 3 | 0.814 | 0.495 | 0.603 |
| Q-7-6 | 2 | 0.831 | 0.449 | 0.561 |
| Q-7-5 | 2 | 0.758 | 0.448 | 0.533 |
| Q-7-4 | 4 | 0.881 | 0.591 | 0.658 |
| Q-7-3 | 3 | 0.897 | 0.536 | 0.611 |
| Q-7-2 | 2 | 0.916 | 0.477 | 0.557 |
| Q-6-5 | 3 | 0.841 | 0.537 | 0.585 |
| Q-6-4 | 2 | 0.860 | 0.479 | 0.543 |
| Q-6-3 | 2 | 0.793 | 0.480 | 0.518 |
| Q-6-2 | 3 | 0.866 | 0.582 | 0.562 |
| Q-5-4 | 2 | 0.884 | 0.528 | 0.519 |
| Q-5-3 | 2 | 0.829 | 0.530 | 0.497 |
Q-5-2 Q-4-3
10-8-4
The tables below detail my power ratings for all possible hands a player might utilize, based on the assumption that they always maintain the two cards with the highest expected value, as outlined in the preceding tables. Certain combinations will never be played, such as unsuited K-6, where the discard is suited with either the K or 6. I adjusted the expected values upwards by 36.9 so that the highest possible hand, A-A with a non-ace discard, carries a value of 100. Of course, actual power ratings will vary slightly depending on the rank of the discarded card, so the values presented here represent a weighted average.
The upcoming table shows the power rating associated with holding a pair. The columns are organized based on whether there is a rank penalty (a scenario where you are dealt a three of a kind), a suit penalty (a singleton matching a card in the pair, hindering flush potential), or no penalty card at all.
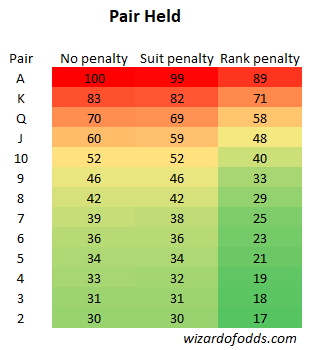
The following table outlines the power ratings for any pairing of two suited cards, where the card being discarded shares the same suit, reflecting a three-card flush situation.
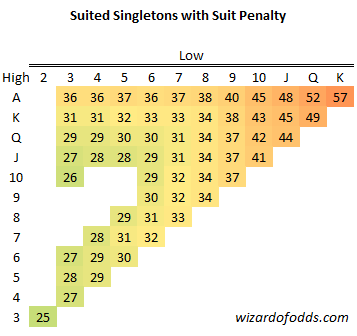
This table presents the power ratings for various combinations of two suited cards when the discarded card belongs to a different suit.
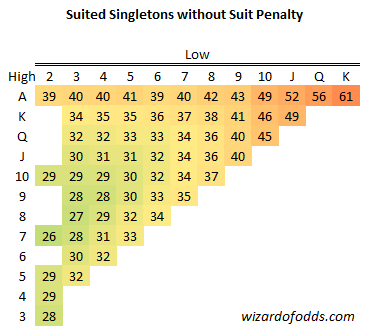
The next table displays the power ratings for combinations of two off-suit cards where the discard is suited to one of the cards, diminishing the chance of achieving a flush.

In the following table, you'll find the power ratings for any combination of two off-suit cards during which the discarded card belongs to a different suit than both, often described as a 'rainbow'—to indicate three different suits.
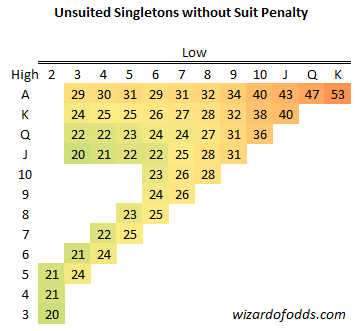
10-7-6
The expected values and strategies outlined on this page emerged from a random simulation methodology. To establish the strategies, I initially crafted a fundamental approach for playing against five 'psychic' opponents—who always play the two cards that maximize the value of the final hand. I then had all five opponents adopt this anti-psychic strategy and developed a revised optimal approach to counter it. This process was repeated four more times, ultimately seeking a Nash equilibrium that could not be enhanced further. The final statistics resulted from a simulation encompassing 6,610,500,000 rounds.









