On this page
Bonus Craps
Introduction
Bonus Craps includes three additional bets that can be placed during a game of craps, detailed below:
- The Small bet wins if the shooter rolls totals between 2 and 6 before rolling a 7, with winning odds typically at 30 to 1.
- The Tall bet wins if the shooter rolls totals from 8 to 12 before hitting a 7, with winnings also generally at 30 to 1.
- The All bet wins if the shooter covers every total from 2 to 12, excluding a roll of 7, before rolling a 7, offering much higher winnings at 150 to 1.
In 2021, I started noticing these bets referred to as 'Diceology' at the Venetian.
Analysis
The table below outlines my findings on the Small and Tall bets, displaying a house edge of 18.30% in the lower right corner.
Small and Tall
| Event | Pays | Probability | Return |
|---|---|---|---|
| Win | 30 | 0.026354 | 0.790617 |
| Loss | -1 | 0.973646 | -0.973646 |
| Total | 1.000000 | -0.183029 |
Historically, some betting tables offered payouts of 34 to 1 for the Small and Tall bets, which have a more favorable house edge of 7.76%.
The table presented below illustrates my analysis of the All bet at a payout of 150 to 1, revealing a house edge of 20.61%.
All
| Event | Pays | Probability | Return |
|---|---|---|---|
| Win | 150 | 0.005258 | 0.788655 |
| Loss | -1 | 0.994742 | -0.994742 |
| Total | 1.000000 | -0.206087 |
I have come across other payout options for the All bet, including odds of 155 and 175 to 1. To translate from 'for one' to 'to one' odds, just subtract one. The table outlines the house edge for payouts divisible by 5 ranging from 150 to 175.
House Edge Summary on All Bet
| Pays | House Edge |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
Methodology
Here are three different methods I've used to analyze Bonus Craps:
- Simulation — This is likely the most straightforward approach, but for someone who appreciates mathematical rigor, simulations sometimes lack intellectual satisfaction.
- Markov Chain — This technique can be somewhat tedious and requires a significant amount of time. Analyzing the Small and Tall bets would need a 6x6 transition matrix, while the All bet demands a 12x12 matrix.
- Integral Calculus — Surprisingly, this method is relatively simple with the aid of an integral calculator, which I will discuss in greater detail shortly.
Instead of thinking of important game events as individual dice rolls, consider them as occurring instantaneously. Assume that the time between events does not affect future occurrences, averaging out to one time unit. This can be conceptualized as an exponential distribution with a mean of 1, although it won't impact the way we evaluate the bet since events still happen sequentially.
The formula below represents the probability that a specific total has not been rolled at least once within a given time span of x:
- 2 or 12: exp(-x/36)
- 3 or 11: exp(-x/18)
- 4 or 10: exp(-x/12)
- 5 or 9: exp(-x/9)
- 6 or 8: exp(-5x/36)
- 7: exp(-x/6)
Let's first analyze the Small bet, keeping in mind that the odds for the Tall bet are identical.
In a timeframe of x units, the probability that the totals 2, 3, 4, 5, and 6 have all been rolled while 7 has not is: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6). The probability of rolling a 7 at time x, given that the player has rolled every total from 2 through 6 previously, is:
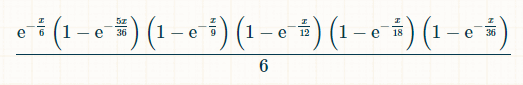
For the integration, I used this integral calculator .
Since a winning 7 could theoretically be rolled at any moment, the probability of winning encompasses the integral of this probability across the interval from 0 to infinity. For those keeping track, the integral, prior to applying the integration limits, is: (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^(-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(-(7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^(-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
Inserting the integration limits yields a result of 20049 divided by 760760, which approximates to 0.02635390924864609.
Next, let's look at the All bet.
In a span of x units, the probability that the totals 2, 3, 4, 5, 6, 8, 9, 10, 11, and 12 have been rolled without a 7 appearing is: (1-exp(-x/36))*exp(-x/6). The chance that, at point x, a player rolls a 7, following previous rolls of every total from 2 to 6, is:2*(1-exp(-x/16))2*(1-exp(-x/12))2*(1-exp(-x/9))2*(1-exp(-5x/36))2As a winning 7 could happen at any point, the probability of winning involves integrating this probability over the interval from 0 to infinity. Again, the integral, before applying the limits, is: (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/18))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10*e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+(54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^(-(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9))/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
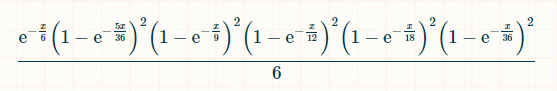
Applying the integration limits results in approximately 126538525259 divided by 24067258815600, equating to 0.0052577040961964420049.
Accurate strategies and insights for casino games such as blackjack, craps, and roulette, among many others, are available.



