On this page
Three Point Molly
Introduction
The Three Point Molly is a unique betting strategy derived from craps. It may be challenging to apply it to other games. The fundamental idea is straightforward: the player places pass or come bets continuously until at least three numbers are secured, enhancing these bets with full odds.
Utilizing the Three Point Molly strategy can give players an impressive house edge of less than 0.5%. This achievement is not necessarily due to the betting technique itself, but rather because the player is making judicious initial bets. I previously utilized this method without knowing it had a specific name.
Rules
The rules that follow assume the player is already familiar with the game mechanics of craps. craps If you’re not acquainted with them, it’s advisable to review the rules regarding pass, come, and odds bets in craps before proceeding any further.
Here’s a brief overview of how to approach the Three Point Molly. Place a pass or come bet for every roll until you have a total of three numbers covered. Additionally, support every pass and come bet with odds, ideally at the maximum multiple permissible.
Now, let’s discuss a more detailed explanation of playing the Three Point Molly.
The player must determine the value of a betting unit, for instance, $10, which should be at least the minimum required for a pass line bet. Each pass or come bet will represent one unit.
- During a come out roll, if the player has fewer than three numbers covered, they should place a pass line bet.
- If it's not a come out roll and there are still fewer than three numbers covered, the player should opt for a come bet.
- Once three numbers are covered, the player should refrain from making any additional bets.
- If a pass or come bet was placed on the previous roll resulting in a point number (4, 5, 6, 8, 9, or 10), it's crucial to back that bet with the odds, ideally at the maximum allowed.
- For any come bets still outstanding during a coming out roll, ensure to turn off the odds.
- Continue this cycle of four steps until a seven occurs, signaling the conclusion of the session.
Analysis
In order to evaluate the effectiveness of the Three Point Molly, I conducted over 32 billion simulated sessions, assuming the player consistently utilized the maximum 3-4-5x odds. Below are some statistics representing what can be anticipated per session, which is defined as playing until the shooter rolls a seven.
- Average units bet: 21.318409
- Average units won: -0.086295
- Ratio money won to money bet = -0.004048
- Average dice rolls = 8.525470
- Probability session win = 0.304783
- Average units won, given a win = 15.880052
- Probability session loss = 0.673288
- Average units lost, given a loss = 7.316730
- Probability session push = 0.021929
- Net points won (excluding come bets during a come out roll) = -0.688804
- Probability of losing three points (excluding come bets during a come out roll) = 0.114039
The spoiler box below contains the raw data displaying the count of net wins from the simulation.
Simulation Results — Net Units Won
| Net Win | Count | Probability |
|---|---|---|
| -28 | 2 | 0.000000 |
| -27 | 7 | 0.000000 |
| -26 | 63 | 0.000000 |
| -25 | 412 | 0.000000 |
| -24 | 2,867 | 0.000000 |
| -23 | 20,077 | 0.000001 |
| -22 | 134,791 | 0.000004 |
| -21 | 869,965 | 0.000027 |
| -20 | 5,283,822 | 0.000163 |
| -19 | 29,276,571 | 0.000905 |
| -18 | 140,054,558 | 0.004330 |
| -17 | 505,734,437 | 0.015637 |
| -16 | 847,665,043 | 0.026209 |
| -15 | 1,070,934,993 | 0.033112 |
| -14 | 670,280,254 | 0.020724 |
| -13 | 352,443,711 | 0.010897 |
| -12 | 278,945,010 | 0.008625 |
| -11 | 739,681,501 | 0.022870 |
| -10 | 1,595,074,146 | 0.049318 |
| -9 | 1,923,363,355 | 0.059469 |
| -8 | 1,717,525,038 | 0.053104 |
| -7 | 1,009,831,502 | 0.031223 |
| -6 | 860,061,437 | 0.026592 |
| -5 | 2,273,628,075 | 0.070298 |
| -4 | 2,532,516,176 | 0.078303 |
| -3 | 2,453,703,762 | 0.075866 |
| -2 | 1,590,852,863 | 0.049188 |
| -1 | 1,177,924,337 | 0.036420 |
| 0 | 709,247,041 | 0.021929 |
| 1 | 418,005,746 | 0.012924 |
| 2 | 348,914,435 | 0.010788 |
| 3 | 474,520,818 | 0.014672 |
| 4 | 659,962,642 | 0.020405 |
| 5 | 746,209,688 | 0.023072 |
| 6 | 670,131,253 | 0.020720 |
| 7 | 453,417,199 | 0.014019 |
| 8 | 281,844,697 | 0.008714 |
| 9 | 217,130,866 | 0.006713 |
| 10 | 261,596,855 | 0.008088 |
| 11 | 365,365,278 | 0.011297 |
| 12 | 431,269,636 | 0.013334 |
| 13 | 402,459,901 | 0.012444 |
| 14 | 290,068,463 | 0.008969 |
| 15 | 190,356,909 | 0.005886 |
| 16 | 148,875,109 | 0.004603 |
| 17 | 168,971,362 | 0.005224 |
| 18 | 222,536,389 | 0.006881 |
| 19 | 258,730,303 | 0.008000 |
| 20 | 243,848,069 | 0.007540 |
| 21 | 183,847,545 | 0.005684 |
| 22 | 126,712,604 | 0.003918 |
| 23 | 100,938,946 | 0.003121 |
| 24 | 109,853,273 | 0.003397 |
| 25 | 137,408,404 | 0.004249 |
| 26 | 156,412,528 | 0.004836 |
| 27 | 148,145,000 | 0.004581 |
| 28 | 115,654,061 | 0.003576 |
| 29 | 83,203,562 | 0.002573 |
| 30 | 67,504,800 | 0.002087 |
| 31 | 71,149,502 | 0.002200 |
| 32 | 85,219,705 | 0.002635 |
| 33 | 94,997,541 | 0.002937 |
| 34 | 90,199,021 | 0.002789 |
| 35 | 72,437,048 | 0.002240 |
| 36 | 54,084,552 | 0.001672 |
| 37 | 44,653,965 | 0.001381 |
| 38 | 45,923,694 | 0.001420 |
| 39 | 53,009,464 | 0.001639 |
| 40 | 57,913,108 | 0.001791 |
| 41 | 55,062,481 | 0.001702 |
| 42 | 45,282,109 | 0.001400 |
| 43 | 34,900,804 | 0.001079 |
| 44 | 29,257,203 | 0.000905 |
| 45 | 29,511,169 | 0.000912 |
| 46 | 33,021,850 | 0.001021 |
| 47 | 35,422,854 | 0.001095 |
| 48 | 33,711,968 | 0.001042 |
| 49 | 28,262,050 | 0.000874 |
| 50 | 22,384,612 | 0.000692 |
| 51 | 19,029,160 | 0.000588 |
| 52 | 18,910,013 | 0.000585 |
| 53 | 20,611,313 | 0.000637 |
| 54 | 21,741,065 | 0.000672 |
| 55 | 20,686,720 | 0.000640 |
| 56 | 17,631,119 | 0.000545 |
| 57 | 14,301,005 | 0.000442 |
| 58 | 12,314,655 | 0.000381 |
| 59 | 12,080,858 | 0.000374 |
| 60 | 12,871,214 | 0.000398 |
| 61 | 13,380,196 | 0.000414 |
| 62 | 12,720,728 | 0.000393 |
| 63 | 10,996,692 | 0.000340 |
| 64 | 9,105,439 | 0.000282 |
| 65 | 7,922,403 | 0.000245 |
| 66 | 7,700,089 | 0.000238 |
| 67 | 8,043,796 | 0.000249 |
| 68 | 8,255,742 | 0.000255 |
| 69 | 7,848,058 | 0.000243 |
| 70 | 6,865,255 | 0.000212 |
| 71 | 5,783,499 | 0.000179 |
| 72 | 5,078,376 | 0.000157 |
| 73 | 4,898,927 | 0.000151 |
| 74 | 5,034,619 | 0.000156 |
| 75 | 5,103,691 | 0.000158 |
| 76 | 4,847,033 | 0.000150 |
| 77 | 4,283,029 | 0.000132 |
| 78 | 3,660,754 | 0.000113 |
| 79 | 3,238,821 | 0.000100 |
| 80 | 3,108,409 | 0.000096 |
| 81 | 3,150,362 | 0.000097 |
| 82 | 3,165,959 | 0.000098 |
| 83 | 2,999,627 | 0.000093 |
| 84 | 2,674,553 | 0.000083 |
| 85 | 2,311,446 | 0.000071 |
| 86 | 2,062,521 | 0.000064 |
| 87 | 1,970,926 | 0.000061 |
| 88 | 1,973,623 | 0.000061 |
| 89 | 1,965,000 | 0.000061 |
| 90 | 1,861,453 | 0.000058 |
| 91 | 1,670,294 | 0.000052 |
| 92 | 1,461,087 | 0.000045 |
| 93 | 1,310,897 | 0.000041 |
| 94 | 1,247,190 | 0.000039 |
| 95 | 1,234,522 | 0.000038 |
| 96 | 1,220,060 | 0.000038 |
| 97 | 1,154,054 | 0.000036 |
| 98 | 1,044,137 | 0.000032 |
| 99 | 920,394 | 0.000028 |
| 100 | 832,175 | 0.000026 |
| 101 | 787,011 | 0.000024 |
| 102 | 773,880 | 0.000024 |
| 103 | 757,517 | 0.000023 |
| 104 | 718,633 | 0.000022 |
| 105 | 653,186 | 0.000020 |
| 106 | 580,952 | 0.000018 |
| 107 | 525,360 | 0.000016 |
| 108 | 497,143 | 0.000015 |
| 109 | 484,725 | 0.000015 |
| 110 | 472,951 | 0.000015 |
| 111 | 445,616 | 0.000014 |
| 112 | 407,531 | 0.000013 |
| 113 | 365,717 | 0.000011 |
| 114 | 332,604 | 0.000010 |
| 115 | 313,971 | 0.000010 |
| 116 | 304,434 | 0.000009 |
| 117 | 295,887 | 0.000009 |
| 118 | 278,744 | 0.000009 |
| 119 | 255,852 | 0.000008 |
| 120 | 230,156 | 0.000007 |
| 121 | 210,020 | 0.000006 |
| 122 | 198,054 | 0.000006 |
| 123 | 189,933 | 0.000006 |
| 124 | 183,510 | 0.000006 |
| 125 | 173,189 | 0.000005 |
| 126 | 159,974 | 0.000005 |
| 127 | 144,554 | 0.000004 |
| 128 | 132,215 | 0.000004 |
| 129 | 124,269 | 0.000004 |
| 130 | 119,071 | 0.000004 |
| 131 | 114,510 | 0.000004 |
| 132 | 108,716 | 0.000003 |
| 133 | 100,078 | 0.000003 |
| 134 | 91,216 | 0.000003 |
| 135 | 83,570 | 0.000003 |
| 136 | 78,006 | 0.000002 |
| 137 | 74,593 | 0.000002 |
| 138 | 72,325 | 0.000002 |
| 139 | 67,766 | 0.000002 |
| 140 | 62,234 | 0.000002 |
| 141 | 57,088 | 0.000002 |
| 142 | 52,607 | 0.000002 |
| 143 | 48,854 | 0.000002 |
| 144 | 46,992 | 0.000001 |
| 145 | 44,948 | 0.000001 |
| 146 | 42,257 | 0.000001 |
| 147 | 39,063 | 0.000001 |
| 148 | 35,878 | 0.000001 |
| 149 | 32,842 | 0.000001 |
| 150 | 30,842 | 0.000001 |
| 151 | 29,896 | 0.000001 |
| 152 | 27,741 | 0.000001 |
| 153 | 26,310 | 0.000001 |
| 154 | 24,503 | 0.000001 |
| 155 | 22,429 | 0.000001 |
| 156 | 20,836 | 0.000001 |
| 157 | 19,530 | 0.000001 |
| 158 | 18,360 | 0.000001 |
| 159 | 17,527 | 0.000001 |
| 160 | 16,597 | 0.000001 |
| 161 | 15,348 | 0.000000 |
| 162 | 13,773 | 0.000000 |
| 163 | 13,047 | 0.000000 |
| 164 | 12,509 | 0.000000 |
| 165 | 11,737 | 0.000000 |
| 166 | 10,958 | 0.000000 |
| 167 | 10,199 | 0.000000 |
| 168 | 9,501 | 0.000000 |
| 169 | 8,880 | 0.000000 |
| 170 | 8,396 | 0.000000 |
| 171 | 7,634 | 0.000000 |
| 172 | 7,399 | 0.000000 |
| 173 | 6,839 | 0.000000 |
| 174 | 6,566 | 0.000000 |
| 175 | 6,050 | 0.000000 |
| 176 | 5,745 | 0.000000 |
| 177 | 5,277 | 0.000000 |
| 178 | 4,783 | 0.000000 |
| 179 | 4,447 | 0.000000 |
| 180 | 4,378 | 0.000000 |
| 181 | 4,001 | 0.000000 |
| 182 | 3,696 | 0.000000 |
| 183 | 3,570 | 0.000000 |
| 184 | 3,243 | 0.000000 |
| 185 | 3,031 | 0.000000 |
| 186 | 2,820 | 0.000000 |
| 187 | 2,688 | 0.000000 |
| 188 | 2,599 | 0.000000 |
| 189 | 2,405 | 0.000000 |
| 190 | 2,228 | 0.000000 |
| 191 | 2,161 | 0.000000 |
| 192 | 1,867 | 0.000000 |
| 193 | 1,756 | 0.000000 |
| 194 | 1,704 | 0.000000 |
| 195 | 1,568 | 0.000000 |
| 196 | 1,439 | 0.000000 |
| 197 | 1,383 | 0.000000 |
| 198 | 1,288 | 0.000000 |
| 199 | 1,210 | 0.000000 |
| 200 | 1,117 | 0.000000 |
| 201 | 1,007 | 0.000000 |
| 202 | 942 | 0.000000 |
| 203 | 917 | 0.000000 |
| 204 | 883 | 0.000000 |
| 205 | 821 | 0.000000 |
| 206 | 719 | 0.000000 |
| 207 | 688 | 0.000000 |
| 208 | 653 | 0.000000 |
| 209 | 612 | 0.000000 |
| 210 | 559 | 0.000000 |
| 211 | 525 | 0.000000 |
| 212 | 511 | 0.000000 |
| 213 | 506 | 0.000000 |
| 214 | 435 | 0.000000 |
| 215 | 395 | 0.000000 |
| 216 | 386 | 0.000000 |
| 217 | 340 | 0.000000 |
| 218 | 336 | 0.000000 |
| 219 | 301 | 0.000000 |
| 220 | 286 | 0.000000 |
| 221 | 277 | 0.000000 |
| 222 | 251 | 0.000000 |
| 223 | 243 | 0.000000 |
| 224 | 228 | 0.000000 |
| 225 | 227 | 0.000000 |
| 226 | 179 | 0.000000 |
| 227 | 180 | 0.000000 |
| 228 | 156 | 0.000000 |
| 229 | 153 | 0.000000 |
| 230 | 142 | 0.000000 |
| 231 | 136 | 0.000000 |
| 232 | 136 | 0.000000 |
| 233 | 130 | 0.000000 |
| 234 | 127 | 0.000000 |
| 235 | 117 | 0.000000 |
| 236 | 113 | 0.000000 |
| 237 | 111 | 0.000000 |
| 238 | 77 | 0.000000 |
| 239 | 99 | 0.000000 |
| 240 | 90 | 0.000000 |
| 241 | 69 | 0.000000 |
| 242 | 74 | 0.000000 |
| 243 | 68 | 0.000000 |
| 244 | 67 | 0.000000 |
| 245 | 55 | 0.000000 |
| 246 | 56 | 0.000000 |
| 247 | 49 | 0.000000 |
| 248 | 50 | 0.000000 |
| 249 | 48 | 0.000000 |
| 250 | 38 | 0.000000 |
| 251 | 37 | 0.000000 |
| 252 | 38 | 0.000000 |
| 253 | 30 | 0.000000 |
| 254 | 23 | 0.000000 |
| 255 | 42 | 0.000000 |
| 256 | 30 | 0.000000 |
| 257 | 16 | 0.000000 |
| 258 | 24 | 0.000000 |
| 259 | 22 | 0.000000 |
| 260 | 15 | 0.000000 |
| 261 | 21 | 0.000000 |
| 262 | 20 | 0.000000 |
| 263 | 16 | 0.000000 |
| 264 | 19 | 0.000000 |
| 265 | 16 | 0.000000 |
| 266 | 10 | 0.000000 |
| 267 | 21 | 0.000000 |
| 268 | 8 | 0.000000 |
| 269 | 16 | 0.000000 |
| 270 | 9 | 0.000000 |
| 271 | 13 | 0.000000 |
| 272 | 8 | 0.000000 |
| 273 | 13 | 0.000000 |
| 274 | 7 | 0.000000 |
| 275 | 4 | 0.000000 |
| 276 | 13 | 0.000000 |
| 277 | 9 | 0.000000 |
| 278 | 5 | 0.000000 |
| 279 | 13 | 0.000000 |
| 280 | 4 | 0.000000 |
| 281 | 4 | 0.000000 |
| 282 | 3 | 0.000000 |
| 283 | 12 | 0.000000 |
| 284 | 6 | 0.000000 |
| 285 | 2 | 0.000000 |
| 286 | 7 | 0.000000 |
| 287 | 2 | 0.000000 |
| 288 | 3 | 0.000000 |
| 290 | 4 | 0.000000 |
| 291 | 1 | 0.000000 |
| 292 | 5 | 0.000000 |
| 294 | 1 | 0.000000 |
| 295 | 2 | 0.000000 |
| 296 | 5 | 0.000000 |
| 297 | 1 | 0.000000 |
| 298 | 1 | 0.000000 |
| 299 | 4 | 0.000000 |
| 300 | 2 | 0.000000 |
| 302 | 4 | 0.000000 |
| 303 | 1 | 0.000000 |
| 305 | 1 | 0.000000 |
| 307 | 1 | 0.000000 |
| 309 | 1 | 0.000000 |
| 310 | 1 | 0.000000 |
| 311 | 1 | 0.000000 |
| 312 | 1 | 0.000000 |
| 313 | 1 | 0.000000 |
| 316 | 1 | 0.000000 |
| 317 | 1 | 0.000000 |
| 318 | 1 | 0.000000 |
| 322 | 1 | 0.000000 |
| 345 | 1 | 0.000000 |
| Total | 32,342,500,000 | 1.000000 |
The chart below illustrates the likelihood of experiencing a net win ranging from -25 to +100 units.
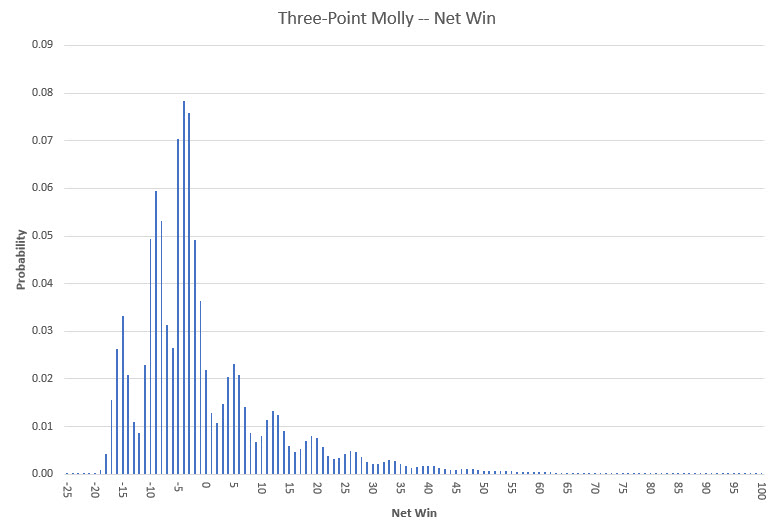
I also performed a separate simulation involving 7.6 billion sessions that focused on net points won, not considering wins on a come out roll (as the odds were turned off). The spoiler button below reveals the findings.
Simulation Results — Net Points Won
| Net Points Won |
Count | Probability |
|---|---|---|
| -3 | 866,696,937 | 0.114039 |
| -2 | 1,799,063,609 | 0.236719 |
| -1 | 2,707,830,104 | 0.356293 |
| 0 | 859,942,908 | 0.113150 |
| 1 | 509,181,625 | 0.066998 |
| 2 | 318,786,035 | 0.041946 |
| 3 | 200,282,777 | 0.026353 |
| 4 | 125,828,052 | 0.016556 |
| 5 | 79,035,018 | 0.010399 |
| 6 | 49,629,205 | 0.006530 |
| 7 | 31,167,223 | 0.004101 |
| 8 | 19,559,543 | 0.002574 |
| 9 | 12,280,517 | 0.001616 |
| 10 | 7,710,235 | 0.001015 |
| 11 | 4,842,391 | 0.000637 |
| 12 | 3,039,626 | 0.000400 |
| 13 | 1,907,701 | 0.000251 |
| 14 | 1,197,193 | 0.000158 |
| 15 | 751,657 | 0.000099 |
| 16 | 471,330 | 0.000062 |
| 17 | 296,874 | 0.000039 |
| 18 | 186,123 | 0.000024 |
| 19 | 116,693 | 0.000015 |
| 20 | 73,449 | 0.000010 |
| 21 | 45,690 | 0.000006 |
| 22 | 28,787 | 0.000004 |
| 23 | 18,141 | 0.000002 |
| 24 | 11,410 | 0.000002 |
| 25 | 7,248 | 0.000001 |
| 26 | 4,395 | 0.000001 |
| 27 | 2,775 | 0.000000 |
| 28 | 1,759 | 0.000000 |
| 29 | 1,081 | 0.000000 |
| 30 | 714 | 0.000000 |
| 31 | 426 | 0.000000 |
| 32 | 276 | 0.000000 |
| 33 | 182 | 0.000000 |
| 34 | 98 | 0.000000 |
| 35 | 69 | 0.000000 |
| 36 | 40 | 0.000000 |
| 37 | 31 | 0.000000 |
| 38 | 20 | 0.000000 |
| 39 | 17 | 0.000000 |
| 40 | 8 | 0.000000 |
| 41 | 2 | 0.000000 |
| 42 | 4 | 0.000000 |
| 43 | 1 | 0.000000 |
| 45 | 1 | 0.000000 |
| Total | 7,600,000,000 | 1.000000 |
Video
Feel free to watch my video discussing the Three Point Molly.
Improving on the Three Point Molly
A player can reduce the overall house edge from 0.405% to 0.374% by activating the odds on a come bet during a come out roll.
Conclusion
In gambling, what truly matters are the games you choose, the bets you place, and sometimes your skill in decision-making, while the motivations behind your bets are often irrelevant. Therefore, betting systems are not some kind of mathematical magic that shifts the odds in the player's favor. In reality, not only do they fail to reduce the house edge, but they don’t even affect it significantly.
The most appealing aspect of the Three Point Molly is not the strategy itself, but rather that it involves bets that carry a very low house edge. Pass and come bets have a house edge of 1.41%, while all odds bets hold a house edge of 0.00%. When averaged together, the overall house edge stands at 0.40%, which is quite difficult to surpass in a casino setting.
Internal Links
Three Point Dolly — An alternative strategy to the Three Point Molly involves placing don't pass, don't come bets, and laying odds. This approach has even better odds than the Three Point Molly, but anticipate some disapproving looks at the tables.
External Links
Let's discuss the Three Point Molly in more depth. in my forum at Wizard of Vegas.


