On this page
Oscar's Grind Betting System
Introduction
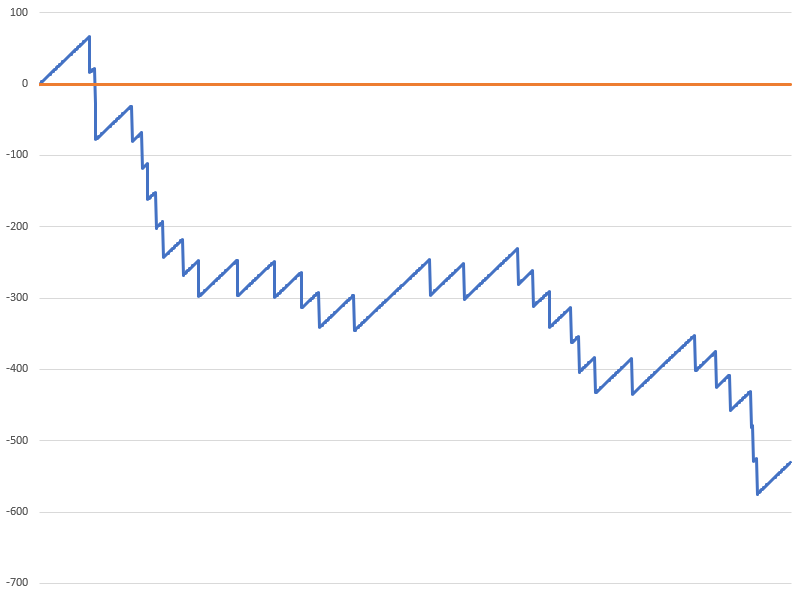
Oscar's Grind is a well-known betting strategy that focuses on achieving a predetermined winning target using even money wagers. While this approach can reach its objective, it often leads to significant losses when it fails. As with all betting systems, its effectiveness diminishes over time and typically results in an overall financial setback.
In contrast to many betting strategies, such as the Martingale, Labouchere or Fibonacci a player strategically increases their bets after securing a win rather than after a loss. Additionally, this method does not escalate the bet amount as rapidly as other systems, resulting in a more measured approach to reaching the desired profit. While this less aggressive strategy may make it harder to hit the winning target, it allows for longer play sessions with a lower average stake.
In general, Oscar's Grind tends to perform well during streaks while struggling in more unpredictable gaming scenarios.
Rules
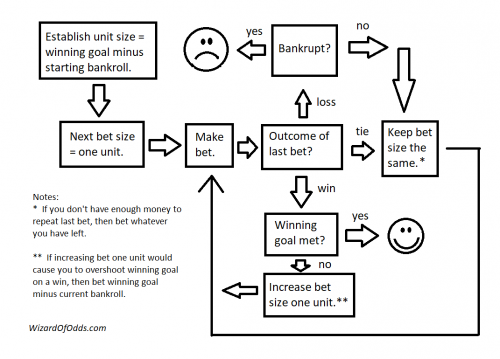
Here’s how to effectively implement Oscar's Grind when placing even money bets.
- The player must establish a target win and set aside a bankroll.
- A one-unit wager is defined to match the predetermined winning target.
- The player makes a one-unit bet.
- If the player encounters a loss or a tie, they will make the same wager again*.
- Upon winning, the player will then increase their subsequent bet by one unit**.
- This process continues until the player either achieves their target win or depletes their entire bankroll.
Footnotes:
*: If the player lacks sufficient funds to repeat the same wager, they will bet whatever amount they have available.
**: If the next win would surpass the target, the player adjusts their bet to equal the winning goal minus their current bankroll.
Take a look at my flowchart for playing the game. Begin at the upper left box. Click on the image for a larger view.
Simulation Results
To illustrate what one can expect from using Oscar's Grind, I created a simulation that adhered to the aforementioned rules across different bets and games. The simulation was executed using a Mersenne Twister random number generator. For each run, the target profit was set to ten units, and I conducted tests using various bankrolls of 10, 25, 50, 100, 250, and 500 units.
The first simulation involved betting on the Player wager in baccarat . This simulation encompassed over 37 billion sessions. Note that the theoretical house edge for the Player wager stands at 1.235%.
Baccarat Simulation — Player Bet
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.17% | 95.65% | 97.69% | 98.77% | 99.46% |
| Average number of bets | 4.736 | 5.697 | 6.230 | 6.646 | 7.067 |
| Average units bet | 6.626 | 10.609 | 14.557 | 19.609 | 28.650 |
| Expected win per session | -0.082 | -0.131 | -0.180 | -0.242 | -0.354 |
| Ratio money lost to Money bet | 1.234% | 1.235% | 1.236% | 1.235% | 1.235% |
The second simulation focused on betting the pass wager in craps . This run included over 45 billion sessions, with the pass bet having a theoretical house edge of 1.41%.
Craps Simulation — Pass Bet
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.14% | 95.63% | 97.67% | 98.76% | 99.45% |
| Average number of bets | 4.289 | 5.161 | 5.645 | 6.024 | 6.409 |
| Average units bet | 6.001 | 9.616 | 13.205 | 17.804 | 26.051 |
| Expected win per session | -0.085 | -0.136 | -0.187 | -0.252 | -0.368 |
| Ratio money lost to Money bet | 1.413% | 1.414% | 1.414% | 1.414% | 1.413% |
Next, the simulation explored the don’t pass wager in craps . This scenario operated over 43 billion sessions, with the house edge for the don’t pass bet being 1.364%.
Craps Simulation — Don't Pass
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.14% | 95.64% | 97.68% | 98.76% | 99.46% |
| Average number of bets | 4.410 | 5.307 | 5.805 | 6.193 | 6.589 |
| Average units bet | 6.171 | 9.887 | 13.574 | 18.296 | 26.768 |
| Expected win per session | -0.084 | -0.135 | -0.185 | -0.250 | -0.365 |
| Ratio money lost to Money bet | 1.364% | 1.364% | 1.364% | 1.364% | 1.364% |
Another simulation was conducted for any even money bet in single-zero roulette, comprising over 43 billion sessions. The theoretical house edge, in this case, is 1/37, which equals 2.703%.
Roulette Simulation — Single Zero
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 89.40% | 95.11% | 97.29% | 98.49% | 99.28% |
| Average number of bets | 4.381 | 5.327 | 5.871 | 6.314 | 6.789 |
| Average units bet | 6.156 | 10.059 | 14.074 | 19.418 | 29.545 |
| Expected win per session | -0.166 | -0.272 | -0.380 | -0.525 | -0.799 |
| Ratio money lost to Money bet | 2.703% | 2.702% | 2.703% | 2.702% | 2.703% |
Yet another simulation covered any even money bet in double-zero roulette, totaling more than 45 billion sessions. The theoretical house edge here is 2/38, or 5.263%.
Roulette Simulation — Double Zero
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 87.81% | 93.93% | 96.39% | 97.81% | 98.81% |
| Average number of bets | 4.567 | 5.670 | 6.350 | 6.944 | 7.646 |
| Average units bet | 6.468 | 10.982 | 15.945 | 23.026 | 37.824 |
| Expected win per session | -0.340 | -0.578 | -0.839 | -1.212 | -1.991 |
| Ratio money lost to Money bet | 5.263% | 5.264% | 5.262% | 5.264% | 5.264% |
Video
Here is my video on Oscar's Grind.
Internal Links
- Labouchere betting system .
- Fibonacci betting system .
- Martingale betting system .
- Anti-Martingale betting system .
- D'Alembert betting system .
- Keefer roulette system .
External Links
Discussion Join the discussion about Oscar's Grind on my forum at Wizard of Vegas.