On this page
Dice Probability
On this page
Introduction
Before engaging in any dice games, it’s beneficial to understand the probability of rolling specific totals. Let's first analyze what happens when rolling two dice. The chart below outlines all six outcomes for the first die in the left column and six outcomes for the second die across the top. The center of the chart displays the combined totals of both dice.
Two Dice Totals
| Die 1 | Die 2 | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The colors in the chart represent how many different combinations can result in each total. To calculate the probability of achieving a specific total, you need to take the number of combinations that result in that total and divide it by the overall total combinations, which is 36. The subsequent table details the exact number of combinations for each total alongside their respective probabilities.
| Total | Number of Combinations |
Probability |
|---|---|---|
| 2 | 1 | 2.78% |
| 3 | 2 | 5.56% |
| 4 | 3 | 8.33% |
| 5 | 4 | 11.11% |
| 6 | 5 | 13.89% |
| 7 | 6 | 16.67% |
| 8 | 5 | 13.89% |
| 9 | 4 | 11.11% |
| 10 | 3 | 8.33% |
| 11 | 2 | 5.56% |
| 12 | 1 | 2.78% |
| Total | 36 | 100% |
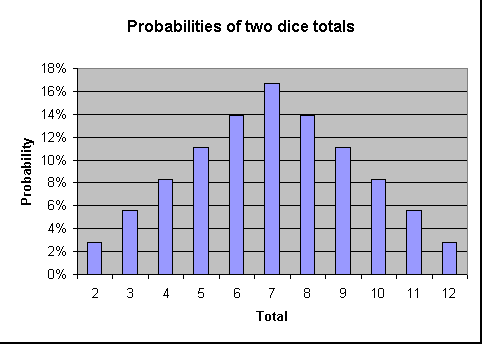
The probability of rolling each possible total is illustrated in the following chart. As you can see, the likelihood of rolling a total increases as it approaches 7.
Online Craps Casino Bonuses View All
The Field Bet Example
With a solid understanding of the probabilities involved in dice throws, we can use this knowledge to analyze the house edge in casino dice games. Take, for example, the field bet in the game. This bet pays out at even money (1:1) if the outcome is a 3, 4, 9, 10, or 11; it offers double the bet (2:1) for rolling a 2 and triples (3:1) for a 12. It’s interesting to note that there are 7 winning totals versus just 4 losing ones, which might mislead someone unfamiliar with the odds into viewing it as a favorable bet. craps A player’s return can be calculated by taking the sum of the products of the probabilities of each event and the net returns associated with those events. The table below lists each possible total with its corresponding net return, probability of occurrence, and average return. Average return is computed by multiplying net return by probability, and the total player return is simply the sum of these average returns.
The final row indicates that the player’s return is -0.0278, meaning that for every dollar wagered, the player can expect to lose approximately 2.78 cents. Consequently, the loss experienced by the player is profit for the house, making the house edge equal to the inverse of the player’s return, which is 0.0278, or 2.78%.
| Total | Net Return | Probability | Average Return |
|---|---|---|---|
| 2 | 2 | 0.0278 | 0.0556 |
| 3 | 1 | 0.0556 | 0.0556 |
| 4 | 1 | 0.0833 | 0.0833 |
| 5 | -1 | 0.1111 | -0.1111 |
| 6 | -1 | 0.1389 | -0.1389 |
| 7 | -1 | 0.1667 | -0.1667 |
| 8 | -1 | 0.1389 | -0.1389 |
| 9 | 1 | 0.1111 | 0.1111 |
| 10 | 1 | 0.0833 | 0.0833 |
| 11 | 1 | 0.0556 | 0.0556 |
| 12 | 3 | 0.0278 | 0.0834 |
| Total | 1 | -0.0278 |
For information on the probabilities involving sums from rolling more than two dice, please refer to my...
Participate in slot tournaments featuring substantial prize pools. probabilities for 1 to 25 dice section.
Poland Recommended Online Casinos
100 % up to
2250zł
+200 spins
Massive gaming platform
Crypto-friendly
Loyalty program
100 % up to
400zł
+100 spins
Bitcoin-friendly
Extra spins
Regular freebies
120 % up to
1200zł
+50 spins
Welcome bonus package
Loyalty Program
The required minimum for deposits and withdrawals is relatively low.
100 % up to
400zł
+120 spins
We accept both traditional currencies and major cryptocurrencies.
Discover mathematically sound strategies and insights applicable to casino games like blackjack, craps, roulette, and countless others you can enjoy.
Live games