On this page
The Truth about Betting Systems
On this page
Introduction
Betting systems not only fail to provide an edge over casino games with an established house advantage, but they don't even manage to reduce it. The behaviors of roulette balls and dice are completely random; each spin or roll occurs independent of previous outcomes. Initially, one may convince themselves that a betting strategy is effective by wagering significant amounts to recoup small gains. However, over time, no system can stand the scrutiny of reality . As you continue to play, the ratio of your losses to your bets will align closely with the expected outcome of that particular game. roulette and every toss in craps Throughout my years managing this website, countless individuals who firmly believe in betting systems have reached out to me via email. Their conviction rivals that of fervent religious believers. Yet, it seems that the more ludicrous a belief, the more tenaciously it is clung to. For centuries, gamblers have sought systems that actually work, yet casinos remain operational and profitable.
not only fall short in outperforming casino games with a built-in advantage, they cannot even make a dent in it
Grand slot tournaments featuring substantial prize pools
 Poland Recommended Online Casinos
Poland Recommended Online Casinos
120 % up to
1200zł
+50 spins
Welcome bonus package
Loyalty Program
Very reasonable minimum amounts for deposits and withdrawals
100 % up to
400zł
+120 spins
Acceptance of both traditional and major cryptocurrencies
A prevalent misconception among gamblers, known as the 'doctrine of the maturity of chances' or 'Monte Carlo fallacy', incorrectly believes that outcomes in games of chance aren't independent and that a sequence of similar results should be offset by contrasting results in the short term. Various 'systems' have emerged based primarily on this misconception, with casinos often encouraging their use and taking advantage of gamblers' ignorance of basic probability and independence principles.
Live games
Gambler's Fallacy
 The biggest gambling myth is that an event that has not happened recently becomes overdue and more likely to occur . This is known as the “gambler’s fallacy.” Thousands of gamblers have devised betting systems that attempt to exploit the gambler’s fallacy by betting the opposite way of recent outcomes. For example, waiting for three reds in roulette and then betting on black. Hucksters sell “guaranteed” get-rich-quick betting systems that are ultimately based on the gambler’s fallacy. None of them work . If you don’t believe me here is what some other sources say on the topic:
The biggest gambling myth is that an event that has not happened recently becomes overdue and more likely to occur . This is known as the “gambler’s fallacy.” Thousands of gamblers have devised betting systems that attempt to exploit the gambler’s fallacy by betting the opposite way of recent outcomes. For example, waiting for three reds in roulette and then betting on black. Hucksters sell “guaranteed” get-rich-quick betting systems that are ultimately based on the gambler’s fallacy. None of them work . If you don’t believe me here is what some other sources say on the topic:
No betting system can transform an unfair game into a lucrative venture. — Encyclopedia Britannica (look under “gambling”)
(second edition, page 94) by Patrick Billingsley Probability and Measure The multitude of so-called 'guaranteed' betting strategies and the spread of myths and misbeliefs surrounding them is overwhelming. There are numerous individuals who adamantly believe in, promote, and defend these systems. Betting strategies represent one of the longest-standing misconceptions in gambling lore, similar to the supporters of perpetual motion machines relentlessly challenging the laws of physics.
The Theory of Gambling and Statistical Logic A thorough analysis of the gambler's fallacy (page 53) by Richard A. Epstein
The Martingale
To illustrate this point, I developed a simulation program that compared the Martingale method against flat betting, both of which were applied to pass line bets in craps (where the winning probability is 49.29%). The Martingale player began with a $1 bet and a bankroll of $255, which could cover up to 8 consecutive losses. Meanwhile, the flat bettor consistently placed $1 bets. The Martingale bettor played for a total of 100 bets or until they could no longer afford the next wager. If the 100th bet ended in a loss, they would keep betting until winning or running out of funds. The flat bettor completed 100 bets each time. I replicated this experiment across 1,000,000 sessions for both strategies and compiled the results. The graph below presents the findings:
From the results, it is evident that the flat bettor’s losses formed a bell curve around a peak loss of $1 without significant deviation. Typically, the Martingale bettor tends to show profits indicated by a bell curve on the far right peaking at $51. However, we also observe occurrences where they couldn’t cover their bets, leading to substantial losses. This scenario occurred in 19.65% of sessions. Many Martingale advocates mistakenly believe that their frequent wins will compensate for the occasional losses.
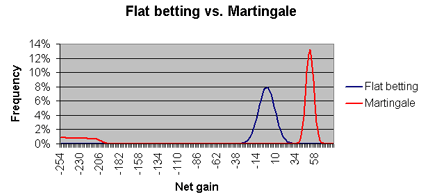
In this study, the average loss per session for the flat bettor was $1.12, while the Martingale bettor experienced an average loss of $4.20. In both scenarios, the ratios of money lost to money won were very similar, being close to 7/495, which corresponds to the
on the pass line bet in craps. This consistency isn’t coincidental. Regardless of the system applied, over time, this ratio will invariably trend toward the house edge. To clarify this, consider a Martingale bettor aiming to win $1 with an initial bet of $1 and possessing a bankroll of $2,047, which can cover up to ten losses in a row. The table below outlines all potential outcomes, along with respective probabilities, expected bets, and returns. house edge The expected bet is calculated by multiplying the total bets by their probabilities, and similarly, the expected return results from multiplying total returns by their respective probabilities. The final row indicates that this Martingale player had an average total bet of 11.81172639 with an average loss of 0.16703451. When we divide the average loss by the average bet, we get .01414141. Dividing 7 by 495 (the house edge on the pass line) yields the same result of 0.01414141! This illustrates that the Martingale strategy offers no advantages or disadvantages compared to flat betting when looking at the expected loss versus expected bet ratio. In essence, all betting methods are equivalent in value when assessed in this manner, reinforcing the notion that none have any real worth.
Previously, I conducted another experiment that supports the findings of the earlier study by testing three different strategies in roulette. The first player adhered to a flat betting strategy of $1 each time, while the second began with $1 and increased the bet by $1 after each win, reverting to $1 if they lost. The third player employed a Martingale approach by doubling their bet after any loss, but like player two, they reverted to a $1 bet after a win. To make the simulation realistic, I capped player three’s maximum bet at $200. Below are the results of this experimentation:
The data reveals that the ratio of money lost relative to money staked closely aligns with the typical house advantage of approximately 1/19, or 0.052632. In summary, altering bet sizes based on recent outcomes has no long-term impact on the results and is equivalent to consistently betting the same amount.
Player 1
- Total amount wagered = $1,000,000,000
- Average wager = $1.00
- Total loss = $52,667,912
- Expected loss = $52,631,579
- Ratio of loss to money wagered = 0.052668
Player 2
- Total amount wagered = $1,899,943,349
- Average wager = $1.90
- Total loss = $100,056,549
- Expected loss = $99,997,018
- Ratio of loss to money wagered = 0.052663
Player 3
- Total amount wagered = $5,744,751,450
- Average wager = $5.74
- Total loss = $302,679,372
- Expected loss = $302,355,340
- Ratio of loss to money wagered = 0.052688
An Old Timer’s Guide to Beating the Craps Table was a betting strategy promising to transform craps games into a reliable source of income. I offered to test this system at no cost. Here are
A Third Experiment
Despite my repeated cautionary messages regarding betting systems, I am frequently approached by readers asking for my recommendations on effective systems. To appease those interested in such methods, I’ve prepared a comprehensive breakdown and analysis of the the results .
The Cancellation Betting System
Betting systems have existed for as long as gambling itself. No system has demonstrated effectiveness . According to sources I've encountered, those selling systems tend to transition swiftly from one strategy to another, often engaging in questionable practices such as copying from one another and attempting to pass off old strategies as new. cancellation betting system .
Don\"t Waste Your Money
 The Internet is full of people selling betting systems with promises of beating the casino at games of luck. Those who sell these systems are the present day equivalent of the 19th century snake oil salesmen. Under no circumstances should you waste one penny on any gambling system. Every time one has been put to a computer simulation it failed and showed the same ratio of losses to money bet as flat betting. If you ask a system salesman about this you likely will get a reply such as, “In real life nobody plays millions of trials in the casino.” You’re likely to also hear that his/her system works in real life, but not when used against a computer simulation. It is interesting that professionals use computers to model real-life problems in just about every field of study, yet when it comes to betting systems computer analysis becomes “worthless and unreliable,” as the salesman of one system put it. In any event, such an excuse misses the point; the computer runs billions of trials simply to prove that a system is unsound. If it won’t work on a computer, it won’t work in the casino.
The Internet is full of people selling betting systems with promises of beating the casino at games of luck. Those who sell these systems are the present day equivalent of the 19th century snake oil salesmen. Under no circumstances should you waste one penny on any gambling system. Every time one has been put to a computer simulation it failed and showed the same ratio of losses to money bet as flat betting. If you ask a system salesman about this you likely will get a reply such as, “In real life nobody plays millions of trials in the casino.” You’re likely to also hear that his/her system works in real life, but not when used against a computer simulation. It is interesting that professionals use computers to model real-life problems in just about every field of study, yet when it comes to betting systems computer analysis becomes “worthless and unreliable,” as the salesman of one system put it. In any event, such an excuse misses the point; the computer runs billions of trials simply to prove that a system is unsound. If it won’t work on a computer, it won’t work in the casino.
System vendors often make outrageous claims about the advantages their products offer. For instance, even a mere 1% edge on an even-money wager could supposedly allow a person to turn $100 into $1,000,000 by betting proportionally to their bankroll. Upon request to substantiate this statement, I created a computer simulation based on the flip of a biased coin showing a 50.5% chance of winning. Throughout this simulation, the player consistently wagered 1% of their bankroll, rounding down to the nearest dollar. If a winning bet pushed their funds over $1,000,000, they only wagered the amount necessary to reach that precise total. I also ran variations with a 2% edge and a starting bankroll of $1,000, detailing the outcomes from all four tests.
Average number of bets required to achieve $1,000,000 = 174,972 (or about 364.5 days, assuming 8 hours of play per day at 60 bets per hour)
$100 Bankroll, 1% Advantage
- Bets won = 7,182,811,698 (50.4999%)
- Bets lost = 7,040,599,544 (49.5001%)
- Player achieved $1,000,000 first = 79,438 (83.019%)
- Player went bust first = 16,249 (16.981%)
- Average number of bets required to achieve $1,000,000 = 63,775 (or approximately 132.9 days, assuming 8 hours of play per day at 60 bets per hour)
$100 Bankroll, 2% Advantage
- Bets won = 7,027,117,205 (51.0000%)
- Bets lost = 6,751,539,769 (49.0000%)
- Player achieved $1,000,000 first = 215,702 (98.099%)
- Player went bust first = 4,180 (1.901%)
- Average number of bets required to achieve $1,000,000 = 137,208 (or roughly 285.8 days, assuming 8 hours of play per day at 60 bets per hour)
$1,000 Bankroll, 1% Advantage
- Bets won = 5,213,026,190 (50.4999%)
- Bets lost = 5,109,817,544 (49.5001%)
- Player achieved $1,000,000 first = 74,818 (99.0285%)
- Player went bust first = 734 (0.9715%)
- Average number of bets required to achieve $1,000,000 = 46,428 (or nearly 96.7 days, assuming 8 hours of play per day at 60 bets per hour)
$1,000 Bankroll, 2% Advantage
- Bets won = 6,332,837,070 (50.9996%)
- Bets lost = 6,084,596,671 (49.0004%)
- Player achieved $1,000,000 first = 267,445 (99.9996%)
- Player went bust first = 1 (0.0004%)
- The results from these simulations indicate that with a minimum advantage of just 1% and a starting bankroll of $100, one could theoretically work their way to a million dollars, akin to compounding interest in finance. Yet, this scenario has never been reported in practice. Could it be that these gambling systems are flawed?
Below are examples of system promoters who seek to exploit those lacking mathematical understanding. Numerous websites of this nature exist online, and this compilation is merely a snapshot. Often, these sites vanish unexpectedly or redirect users to unrelated content. Please inform me if any of these links malfunction or lead to inappropriate destinations.
Uncovering the Reality of Betting Strategies - Wizard of Odds
Find the Top Online Casinos Available in Your Region
The Wizard of Odds Challenge
Calculate Your Lottery Jackpot Ticket Sales with Precision rules of the challenge Betting strategies don’t just fail to overcome the inherent advantage of casino games; they can’t even make a noticeable impact. The outcomes in games like roulette or dice are entirely random and have no connection to previous results. Each spin or roll stands alone in its outcome.
While you might trick yourself into believing a betting strategy is effective in the short term by risking substantial amounts for minimal gains, over time, no strategy holds up against the realities of probability . The longer you engage in play, the closer your losses will align with the expected outcomes set by the odds of the game. VegasClick.com Throughout my years managing this website, I've received countless messages from those who are firm believers in betting strategies. Their conviction often resembles religious zeal. Yet, the more absurd a belief is, the more fiercely it tends to be held onto. For centuries, gamblers have searched for a successful betting strategy, yet casinos continue to thrive.
A Fourth Experiment
cannot surpass casino games that are designed with a house edge, and they can’t even make a small dent challenge Exciting slot competitions with enormous prize pools Rainsong Challenge page for all the details.
Please, Don\"t Write
Minimum deposit and withdrawal amounts are quite reasonable Gambling FAQ .
Both traditional and popular cryptocurrencies are accepted Wizard of Vegas A well-known misconception among gamblers, referred to as the doctrine of the maturity of chances (or Monte Carlo fallacy), falsely believes that each outcome in a game of chance is influenced by previous results. This belief leads gamblers to create various “systems” based on this flawed thinking; casino owners are more than happy to encourage the use of these systems and take advantage of any oversight regarding the fundamental rules of probability and the independence of each play.
No betting strategy can transform a game with a built-in disadvantage into a winning venture..
| Jackpot | Value | Break-even | RTP | Software | |
|---|---|---|---|---|---|
| Rocket Jacks | $140,863 | $9,426 | 165.4% | Saucify | Play |
| Triple Sevens Blackjack | $258,634 | $109,862 | 151.4% | Microgaming | Play |
| SupaJax | $163,266 | $52,417 | 120.2% | Microgaming | Play |
| Poker Ride | $283,627 | $218,047 | 119.2% | Microgaming | Play |
| Jackpot Deuces | $186,793 | $53,982 | 115% | Microgaming | Play |
| Jackpot Joker Poker | €161,518 | €185,903 | 98.7% | Proprietary | Play |
| Caribbean Stud Poker | $75,003 | $201,245 | 97.4% | Real Time Gaming | Play |
| Progressive Jacks or Better | £4,396 | £17,477 | 96.7% | Gamesys |
Internal Links
- Oscar's Grind betting system .
- Labouchere betting system .
- Fibonacci betting system .
- Martingale betting system .
- Anti-Martingale betting system .
- D'Alembert betting system .
- Keefer roulette system .
- 1-3-2-6 Betting System .
- 2-1-2 (Manhattan) Betting System .
- Three Point Molly Betting System .
- Three Point Dolly Betting System .
- Rothstein Betting System .
Related Reading
- (second edition, page 94) by Patrick Billingsley
- The sheer number of 'surefire' betting systems, combined with the abundance of myths and misunderstandings surrounding them, leads to a vast community of supporters who staunchly believe in these systems. Betting systems represent one of the oldest misconceptions prevalent in gambling culture. Those who endorse these systems are akin to believers in perpetual motion machines, ignoring the fundamental laws of physics.
- The Statistical Logic Behind Gambling and Its Theory
- Real Casinos, Real Money
- Guide to No-Deposit Bonuses
External Links
- Betting Systems and the House Edge a thorough examination of the gambler's fallacy
- Betting Systems Each week, I receive a few inquiries from individuals curious about a betting strategy where a player doubles their wager following a loss. This approach is typically used in games with even odds, such as betting on red or black in roulette or the pass/don't pass in craps, and it is known as the Martingale. The premise is that by doubling the bet after losing, you will eventually win enough to cover previous losses and make a profit of one unit. For instance, if someone starts with a bet of $1 and loses four consecutive times but wins on the fifth, they will have lost a total of $15 but won $16 in the end, thus recovering their losses and achieving a $1 profit. However, it’s crucial to note that losing multiple bets in succession is easier than one might think, often leading to depleting the betting funds.
- Debunking To illustrate this, I developed a simulation program that tested two strategies: the Martingale and flat betting, both applied to the pass line in craps (with a winning probability of 49.29%). The Martingale strategist began with a $1 bet and had an initial bankroll of $255, sufficient to endure up to eight consecutive losses. The flat bettor consistently wagered $1 each time. The Martingale player aimed for 100 bets, or would continue until unable to place further bets. In instances where the 100th bet was a loss, they would persist until winning or could no longer afford the next wager. Meanwhile, the flat bettor would complete a set of 100 bets every time. I repeated this process over 1,000,000 sessions for both betting types and compiled the results. The graph below illustrates these findings:



