Video Poker - Other Games
Hi Michael, I've recently tried a variant of video poker called \"Triple Play.\" This particular machine allows players to engage with three hands simultaneously, carrying over the cards from the first hand into the other two. For instance, if you hit four of a kind on the initial five-card draw, you'd receive payouts for all three hands. I feel like this variant offers a better chance of winning compared to traditional jacks-or-better. Is that just my perception? I appreciate your insights.
The expected returns on a triple play machine are equivalent to those on a single-hand machine, provided that the payout tables remain the same.
What are the odds of receiving a royal flush on a Triple Play video poker machine? It happened to me last week, and I was absolutely shocked!
In any 52-card video poker game, the likelihood of being dealt a natural royal flush is 1 in 649,740.
Where can I find a guide related to strategies for playing Pick 'em poker?
You can buy the video poker strategy master This guide can provide effective strategies for this game and for most other variations of video poker.
Do you have any tips or opinions on Spin Poker? The developers suggest using a strategy similar to that of jacks-or-better (if playing jacks-or-better SP). I've played it at the Claridge, and it seems that the arrangement of your held cards influences the game, particularly if they're clustered or spread out. Additionally, I think expanding your coverage of multi-play machines would be beneficial since their popularity is rapidly increasing, and some players are experiencing significant losses. I've also encountered some triple play draw poker machines with unfavorable odds like 6/5 at places such as the Tropicana in Atlantic City, which is truly not recommended for video poker! Thanks for your valuable site!
IGT's advice to apply the same strategy for Spin Poker as you would for single line video poker is accurate. Statistically, the odds remain consistent. However, Spin Poker does possess higher volatility owing to the fact that nine different lines often share many of the same cards. This volatility also applies to multi-play video poker; the strategies and returns mirror those of a single line game. I delve into the volatility aspects of multi-play video poker in my resources. video poker appendix 3 .
Whenever I'm in Las Vegas, I often play video Double-Down Stud. I'm curious how the total return of these machines stacks up against various video poker formats. The machines located at the Riviera (one of the limited venues I've encountered that offers these machines) feature the following payouts:
One-coin pay table
--------------------
Pair, 6-10’s 1
Pair, J-A’s 2
2 Pair 3
3 of a Kind 4
Straight 6
Flush 9
Full House 12
4 of a Kind 50
Straight-Flush 200
Royal Flush 1,000
2-5 coins, multiply 1-coin payout
5-coin Royal pays 20,000 coins
What would the return be for these machines with optimal play?
As a side note, these machines accumulate slot points at the same rate as video poker (which is half the rate of standard slots), but I find that I gather points more rapidly due to the clear double-down opportunities. Does this have an indirect positive effect on returns?
I really appreciate your website! Thank you!
With this payout structure, the house edge stands at 2.10%, while the player’s return is 1.68%. The strategy remains consistent with what I've detailed in my resources. element of risk For instance, consider being dealt four cards that are relevant to a flush (like four spades). In triple play video poker, you can potentially receive the same card three times, one for each line (imagine drawing the 2 of spades to complete three flushes). However, in Spin Poker, you can't 'replace' cards — meaning, I couldn’t receive the 2 of spades across all three lines. Does this alter the strategic approach, or is it balanced out by the multiple lines available for winning? Double Down Stud No, the strategic approach remains unchanged. The odds and strategies are identical whether replacement cards come from a single deck or from different decks for each hand. However, a game like Spin Poker may have less volatility since all replacement cards originate from the same deck.
My spouse and I regularly play Aces and Faces in Tunica, MS. We have adopted the basic Jacks or Better strategy recommended on your site. Is this the most effective strategy for this game? If not, could you guide us toward the optimal strategy for it? Thank you.
Certainly! You can utilize nearly optimal strategies for almost any game with tools like Video Poker Strategy Master or Frugal Video Poker.
The Fremont Street in downtown Vegas offers a video poker option called Treasure Chest. It’s essentially Jacks or Better with a full payout table, except there’s a twist — if you bet the maximum coins and land four of a kind, you access a bonus screen where you can choose from five treasure chests, which have coins worth 120, 160, 320, 640, or 1,000. How does this impact the theoretical return, and does it modify the optimum strategy? From my experience, I find that the lower denominations seem to appear frequently, while the more valuable ones are harder to come by. I suspect the value of the chest may depend on the speed at which you select it once reaching that screen.
I've encountered this game. To my understanding of gaming regulations, it’s allowed to have the minor prizes appear more frequently than the major ones. The best strategy would be to calculate the average payout for a four of a kind and then use an appropriate program to determine the optimal return. For strategy recommendations, you could use Video Poker Strategy Master or Frugal Video Poker and input the specific pay table.
Should I steer clear of the 50-play (or even the 100-play) video poker machines? I find myself drawn to them, but they really drain my finances. What insights can you offer?
In general, 50 and 100-play machines tend to have poor payout tables which makes them less desirable. However, if you happen to find a decent pay table, consider what you'd play at a single-play machine and adapt that figure by dividing it by 50 or 100. For example, if you typically play the single-line machines at $1, you should opt for 2-cent games on the 50-play or 1-cent games on the 100-play.
I recently read your article on Anything’s Wild. I’m curious — how can a player achieve a Natural Royal Flush if they opt for a 10, Jack, Queen, King, or Ace as their wild card? If T, J, Q, K, or A are set as wild, how does a 'natural' royal differ from a 'wild' royal?
I don’t specifically recall this in the rules, but I would assume it's similar to One Eyed Jacks wherein a wildcard is not automatically forced to behave as wild if the player can naturally form a royal flush.
I was reviewing your video poker section and noted the 'Full Pay' Deuces Wild game, touted to have a 100.76% return with optimal strategy. However, I’ve also come across the 'Sevens Wild' game from RTG that I played on Inet-Bet and Bodog. This particular pay table matches that of the 'Full Pay' Deuces Wild, except for the Straight Flush, which pays 10 for 1 instead of 9 for 1. Shouldn't this logically lead to an expected return exceeding 100.76%, rather than the 99.11% stated previously? Am I missing a vital piece of information here?
The reason the Deuces Wild variant offers a better payout is that a deuce is generally not as high in value as a seven. This is due to the greater number of ways to construct straights and straight flushes around a seven. Therefore, designating deuces as wild creates a more significant change compared to making sevens wild. As I explain in my sections, with identical pay tables, making deuces wild yields a return of 96.76%, while the return for sevens wild is only 94.13%.
There's a machine with a $10,100 royal jackpot. It’s a dollar machine, and with a payout percentage of only 94%, it could severely impact my bankroll. I know that as jackpots rise, so too does the payout percentage. Yet, without the jackpot, I wouldn’t even consider playing this machine. Is it worthwhile to give it a try? The floor manager mentioned that it's spiked as high as $12,000 in the past. Should I take the chance or stick to safer bets?
The return for the 6/5 double double bonus is exactly 0.946569. According to my table, the probability of hitting a royal is 0.000025. I prefer to utilize more precise figures, so let’s calculate the return by dividing the win rate, which is 0.020297/800 = 0.00002537. The return for all wins excluding the royal totals 0.926273. Let’s denote the break-even jackpot amount as j. Solving for j: Anything’s Wild The 2,906 is measured in betting units. For a dollar machine ($5 total bet), the break-even point would translate to $5*2,906 = $14,530. Therefore, the $12,000 is still significantly far from the break-even point. For those perfectionists wanting to know, as the progressive amount increases, the optimal strategy shifts to play more aggressively for royals, though my answer assumes the player maintains the same 6/5 optimal approach continuously.
There is 6/5 Double Double Bonus Poker A useful generalization for any 52-card video poker game is to add 0.5% for every additional 1,000 coins on the meter. In this case, with a $10,100 meter, that's $6,100 more than a non-progressive. Since it's a dollar game, that's equated to 6,100 coins, which means we would add 0.5% × (6,100/1,000) = 3.05% to the base return. The base return being 92.63% indicates that the total return might be approximated at 94.66% + 3.05% = 97.71%. For the actual return on a $10,100 meter, it stands at 97.75%, which is quite close.
double double bonus poker strategy section
1 = 0.926273 + 0.00002537*j
j = (1-0.926273)/ 0.00002537 = 2,906.
In double-double bonus, the payout for a straight flush is 50, for a flush it's 6, and for a straight, it’s 4. The chances of achieving the straight flush are 2/47, for a flush it's 7/47, and for a straight, it’s 5/47. Consequently, the expected return when discarding the 9
while there's a promotion that adds $250 to each taxable jackpot. The machines also feature a double-up option, which I’m using for each full house or better until I either lose or surpass $1200. Can you help in calculating the expected value for this setup? Thanks.
On your video poker Great find! You didn’t mention what denomination you are playing, which is crucial, so I’ll assume they’re dollars. For a maximum bet of five coins, the number of doubles needed to achieve a win of w (where w < 1200) would be 1 + int(log(1200) - log(w)) / log(2). , you state that if you are dealt 5 6
6 7
7 8
8 9
9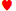 , that it is correct to hold the straight. It just seems counter-intuitive to me, but if you could explain in a little more detail about why going for the straight flush is poor strategy, I would be grateful.
, that it is correct to hold the straight. It just seems counter-intuitive to me, but if you could explain in a little more detail about why going for the straight flush is poor strategy, I would be grateful.
The following table illustrates, for each opening hand, the initial win before doubling, the pre-double probability, the number of doubles necessary, the winning amount post-double, and the likelihood of achieving this post-double win, including the $250 bonus. The final cell indicates a return of 115.5%. Hence, on average, you can expect to hit a jackpot every 297 hands, with an average jackpot value of $1,717.46. is (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468. The expected return of the straight at 4 is much more.
is (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468. The expected return of the straight at 4 is much more.
I am playing 8-5 triple bonus plus 8-5 Triple Bonus Return Table that includes a $250 Bonus for Wins of $1,200 or More
What is considered the loosest video poker game currently available in Vegas?
Video Poker - Alternative Games - Wizard of Odds
Explore the Top Online Casinos Available in Your Region
| Pre-Double Win | Pays | Pre-Double Probability | Doubles Required | Post-Double Win | Post-Double Probability | Return |
| Royal flush | $4000 | 0.000026 | 0 | $4250 | 0.000026 | 0.02193 |
| Peter from Ottawa, Canada | $500 | 0.000118 | 2 | $2250 | 0.00003 | 0.013322 |
| David B. from El Cajon, California | $1200 | 0.000235 | 0 | $1450 | 0.000235 | 0.068227 |
| Frank | $600 | 0.000542 | 1 | $1450 | 0.000271 | 0.078557 |
| You can buy the | $250 | 0.001629 | 3 | $2250 | 0.000204 | 0.091637 |
| video poker strategy master | $40 | 0.010546 | 5 | $1530 | 0.00033 | 0.100842 |
| Jef from Atlantic City, US | $25 | 0.011055 | 6 | $1850 | 0.000173 | 0.063913 |
| video poker appendix 3 | $20 | 0.012738 | 6 | $1530 | 0.000199 | 0.060902 |
| One-coin pay table | $15 | 0.075542 | 7 | $2170 | 0.00059 | 0.256136 |
| -------------------- | $5 | 0.123065 | 8 | $1530 | 0.000481 | 0.147101 |
| Pair, 6-10’s 1 | $5 | 0.211575 | 8 | $1530 | 0.000826 | 0.252898 |
| Pair, J-A’s 2 | 0.447071 | 0 | 0 | 0.003364 | 1.155465 |
Calculator for Evaluating Lottery Jackpot Ticket Sales

Attend exciting slot tournaments featuring substantial prize pools 3 of a Kind 4 Hi, Michael. I recently tried a video poker variant known as 'Triple Play'. This machine permits players to engage with three hands simultaneously, carrying forward the cards from the first hand to the next two. For instance, if you draw four of a kind in the first hand, you earn payouts across all three hands. I have a feeling that the chances of winning might be better on this type of machine compared to the classic jacks-or-better format. Is this perception accurate, or just a mirage? I appreciate any insights you can provide.
The expected returns on the triple play machines are equivalent to those of single-hand machines, provided the pay tables are the same. Straight 6 What are the probabilities of receiving a royal flush while playing on a Triple Play video poker machine? This happened to me recently, and I was stunned!
In a standard 52-card video poker game, the likelihood of being dealt a natural royal flush is approximately 1 in 649,740.
Could you direct me to a strategy guide for Pick 'em poker? Full House 12 which can craft an excellent strategic approach for this specific game, along with many other variations of video poker. 4 of a Kind 50 Straight-Flush 200
Do you have any insights or tips regarding Spin Poker? The game developers suggest that players follow the same strategy as for jacks or better when playing the jacks or better version of Spin Poker. I tried it at the Claridge, and it seems that how the cards are grouped or spread can significantly impact the outcomes. Additionally, I believe it would be beneficial if you expanded your coverage of n-play machines, as they're becoming increasingly popular and some players are incurring significant losses on them. I've noticed some triple play draw poker machines at 6/5 payouts that can be quite detrimental, especially at the Tropicana in Atlantic City, which I'd advise against for video poker. Appreciate the fantastic resource you provide!
| Royal Flush 1,000 | 2-5 coins, multiply 1-coin payout | 5-coin Royal pays 20,000 coins |
| Tim from Newburgh, New York | 0.990675 | 0.503768 |
| element of risk | 0.991390 | 0.494518 |
| Double Down Stud | 0.991660 | 0.455145 |
| Tim from Chicago, Illinois | 0.995439 | 0.454565 |
| Vance & Ashley Dennis | 0.989808 | 0.447163 |
| anonymous | 0.994179 | 0.442807 |
| anonymous | 0.984425 | 0.441435 |
| anonymous | 0.991065 | 0.431893 |
| Ken from Tallahassee, Florida | 0.989562 | 0.370122 |
| Anything’s Wild | 0.991981 | 0.300874 |
IGT's stance on employing the same strategy for Spin Poker as for single-line video poker is correct. Statistically, the odds remain the same. However, Spin Poker exhibits increased volatility due to nine different lines sharing many of the same cards. The same principle applies to multi-play video poker, where the strategy and return align with single-line games. I delve into the volatility associated with multi-play video poker in my work.
When I’m in Las Vegas, I often try out the video Double-Down Stud. I'm interested in how the overall return of these machines stacks up against the various types of video poker available. The machines at the Riviera (one of the few venues where I’ve encountered them) offer the following payouts:
Double Double Bonus Poker
| Nathan from Edina, MN | 1 = 0.926273 + 0.00002537*j | j = (1-0.926273)/ 0.00002537 = 2,906. | On your video poker | , you state that if you are dealt 5 |
|---|---|---|---|---|
| David from Montego Bay | 800 | 490,090,668 | 0.000025 | 0.019669 |
| I am playing 8-5 | 100 | 2,417,714,292 | 0.000121 | 0.012129 |
| triple bonus plus | 800 | 4,936,967,256 | 0.000248 | 0.198140 |
| Robert from Biloxi, MS | 80 | 10,579,511,880 | 0.000531 | 0.042460 |
| Pre-Double Win | 50 | 31,662,193,440 | 0.001588 | 0.079421 |
| Pays | 10 | 213,464,864,880 | 0.010709 | 0.107090 |
| Pre-Double Probability | 5 | 280,594,323,000 | 0.014077 | 0.070384 |
| Doubles Required | 4 | 276,071,121,072 | 0.013850 | 0.055399 |
| Post-Double Win | 3 | 1,470,711,394,284 | 0.073782 | 0.221346 |
| Post-Double Probability | 1 | 2,398,705,865,028 | 0.120337 | 0.120337 |
| Return | 1 | 1,307,753,371,584 | 0.065607 | 0.065607 |
| Royal flush | 0 | 13,935,843,099,816 | 0.699126 | 0.000000 |
| Peter from Ottawa, Canada | 19,933,230,517,200 | 1.000000 | 0.991982 |
What’s the return rate for these machines when played correctly?
By the way, these machines generate slot points at the same rate as video poker (which is half that of regular slot machines), but I notice that I accumulate points quicker due to the frequent double-down scenarios. Does this have any indirect effect on the return?
David B. from El Cajon, California
| Frank | You can buy the | video poker strategy master | Jef from Atlantic City, US | video poker appendix 3 |
|---|---|---|---|---|
| One-coin pay table | 800 | 439,463,508 | 0.000022 | 0.017637 |
| -------------------- | 50 | 2,348,724,720 | 0.000118 | 0.005891 |
| Pair, 6-10’s 1 | 800 | 1,402,364,496 | 0.000070 | 0.056282 |
| Pair, J-A’s 2 | 400 | 3,440,009,028 | 0.000173 | 0.069031 |
| 2 Pair 3 | 160 | 2,952,442,272 | 0.000148 | 0.023699 |
| 3 of a Kind 4 | 80 | 6,376,626,780 | 0.000320 | 0.025592 |
| Straight 6 | 50 | 31,673,324,076 | 0.001589 | 0.079449 |
| Flush 9 | 9 | 206,321,656,284 | 0.010351 | 0.093156 |
| Full House 12 | 7 | 311,320,443,672 | 0.015618 | 0.109327 |
| 4 of a Kind 50 | 4 | 252,218,322,636 | 0.012653 | 0.050613 |
| Straight-Flush 200 | 2 | 1,468,173,074,448 | 0.073655 | 0.147309 |
| Royal Flush 1,000 | 1 | 2,390,581,734,264 | 0.119929 | 0.119929 |
| 2-5 coins, multiply 1-coin payout | 1 | 3,944,045,609,748 | 0.197863 | 0.197863 |
| 5-coin Royal pays 20,000 coins | 0 | 11,311,936,721,268 | 0.567491 | 0.000000 |
| Tim from Newburgh, New York | 19,933,230,517,200 | 1.000000 | 0.995778 |
I truly enjoy your website! Thank you! element of risk .
According to this pay table, the house edge is 2.10%, and the
- Double Down Stud
- Tim from Chicago, Illinois
- Vance & Ashley Dennis
anonymous
- anonymous
- is set at 1.68%. The optimal strategy is as detailed in my
- section. Factoring in the raise towards cash back is equivalent to receiving an additional 25% on cash back based on the initial wager alone.
Suppose you receive 4 cards to a flush (like 4 spades). In triple play video poker, you’re able to draw the same card up to three times, once for each hand (like pulling the 2 of spades across three flushes). However, in Spin Poker, there isn't a 'replacement' mechanism – you can't end up with the 2 of spades on all three lines. Does this alter the strategy, or is the potential number of winning lines a counterbalance?
No, the strategy remains unchanged. The odds are linked to the strategy, whether all replacement cards originate from the same deck or each hand utilizes a different deck. However, games like Spin Poker, utilizing a single deck for all replacement cards, may result in less volatility.
My wife and I frequently play Aces and Faces at Tunica, MS. We’ve been using the basic Jacks or Better strategy as suggested on your website. Is this indeed the best approach for this specific game? If it’s not, could you share what the optimal strategy would be?
Absolutely not! You can find nearly optimal strategies for just about any game through Video Poker Strategy Master or Frugal Video Poker. The Fremont in downtown Las Vegas features a video poker variant called Treasure Chest. Essentially, it's Jacks or Better but with a full pay table, plus one significant twist – if you wager the maximum coins and hit four of a kind, you are taken to a bonus selection screen where you can choose from five treasure chests. These chests contain prizes of 120, 160, 320, 640, or 1,000 coins. How does this influence the theoretical return, and does it necessitate a change in the optimal strategy? Based on my gameplay, I usually receive 120 coins most of the time, with 160 being somewhat rare. It seems the chest's value might depend on how swiftly you choose your chest after reaching that bonus screen. I’m familiar with this game. From what I understand about gaming regulations, it’s acceptable for lower prizes to have a higher probability than the larger ones. To determine your best bet, you could estimate the average payout for a four of a kind and process that through an appropriate program for the optimal return. To develop a strategy, you can utilize Video Poker Strategy Master or Frugal Video Poker by entering any pay table.


