Video Poker - Deuces Wild
I reviewed the expected returns for the different payout structures in Deuces Wild, yet I couldn't find the specific payout structure I was interested in. Could you provide the anticipated payout for a Deuces Wild setup with the following parameters:
Royal flush - 840
Four deuces - 200
Wild Royal - 20
Five of a kind - 12
Straight flush - 9
Four of a kind - 5
Full house - 3
Flush - 2
Straight - 2
Three of a kind - 1
I would handle this task myself, but I'm not able to access the required software since I don't use Windows.
The return is 99.0251%.
I observed that in your comprehensive strategy guide for Full Pay Deuces Wild, having one pair (without a deuce) is prioritized over having two pairs. Does this imply that when dealt two pairs, I should consistently discard three cards and retain only one of the pairs? If so, how do I determine which pair to keep?
Yes, you should indeed retain only one of the two pairs. The sole exception to this rule regarding two pairs is when you also have three cards that could form a royal flush. It doesn't matter which pair you decide to keep. This is one of the few scenarios in skill-based games where the player has some flexibility in their choice. Personally, I tend to keep the higher pair to avoid wasting time making a decision.
How should I approach these particular hands in Deuces Wild video poker when both a flush and four of a kind offer a payout of 4 to 1? (1) two pair, (2) a deuce along with two suited high cards.
I’ll assume the rest of the payout structure matches that of. full pay deuces wild In this scenario, for (1) you should keep the two pair, and for (2) retain the deuce and both high cards.
Are there any online casinos that feature looser Deuces Wild rules, and which ones offer the best payouts for this variant? Thank you.
Atlantic Interbet provides full pay Deuces Wild with a return of 100.77%. Their maximum coin denomination for this game is 50 cents.
While running your Deuces Wild video poker program, I ended up with these cards: QJ8 of spades and T7 of diamonds. I chose the four-card inside straight draw, keeping the QJT8. However, the advice feature suggested I retain the JT87 and discard the Q. This situation seems to present two viable plays with equal expected value, similar to the case when deciding which of two pairs to keep.
You are correct. There are indeed two possible routes to pursue an inside straight, both yielding the same expected value. I apologize if my program indicated otherwise; I will make sure to fix that.
This website is fantastic and packed with useful information. While reviewing the plays in Deuces Wild video poker, I came across the term 'penalty card' and didn’t quite grasp its meaning. Could you clarify this for me?
I appreciate your kind words! I've just updated my explanation regarding penalty cards. I believe that novice players should avoid strategies that take penalty cards into account. However, for those aiming to play nearly flawlessly, here’s my definition: 'A penalty card is a potentially beneficial card that is discarded. For instance, if a player has three cards towards a royal flush and four cards towards a flush, the correct move is to maintain the three towards the royal while discarding the extra suited card. This discarded suited card is considered a flush penalty card since it could have completed a flush. By letting it go, the player's chances of making a flush are 'penalized.' Sometimes, penalty cards can influence marginal plays. For example, if a player holds a suited 10 and king with no additional suited cards, nor a 9, jack, queen, or ace, they should keep the two toward a royal flush. However, keeping these is only slightly better than discarding everything. If the player has just one suited card or any card that could aid in creating a straight, then the odds of forming a flush or straight decrease, making the overall expected return lower than that of discarding all cards. Thus in such cases, players need to be cautious about the impact of penalty cards.'
I went to play Deuces Wild video poker and noticed a considerable difference in payout odds across various machines. None of the odds matched what you've analyzed as favorable for the player. Did the casinos possibly alter the odds because they noticed your winning strategies? If that’s true, I sincerely appreciate your insight!
I don't think I can be held directly accountable, but it could be suggested that gambling experts, particularly Bob Dancer, have influenced the state of video poker. Nevertheless, if it weren't for experts sharing proper strategies, only a select few would ever learn how to play effectively.
I have an intriguing calculation to share. During a session of Deuces Wild Video Poker, I was dealt what can be described as 'Garbage.' After discarding all five cards, I was dealt 4 deuces on the draw, earning 1,000 coins! What are the odds of 4 deuces appearing after discarding all 5 cards? Thanks for your assistance, and keep up the great work on your site! P.S. On the same machine, I switched to Deuces Wild Bonus Poker and was dealt 3 wilds with 4 and 5 of diamonds (which made a straight flush). I got rid of the 4 and 5 and ended up with 4 deuces plus an Ace for another 2,000! Lucky day at Soboba Casino in Southern California.
Absolutely! There are combin(47,5)=1533939 possible ways to draw 5 cards from the remaining 47 in the deck. Out of these, 43 scenarios will yield four deuces (since the 5th card has 43 possibilities, excluding the four deuces). Therefore, the likelihood of drawing four deuces is 43/1533939 = 1/35673 = 0.000028032. The probability of drawing a fourth deuce after having kept 3 is calculated as (47-1)/combin(47,2) = 46/1081 = 0.0426. In my examples, you can observe how the probability distribution works in Deuces Wild concerning the number of cards drawn for any given hand. For instance, about 2.62% of all four deuces will come from drawing all four. The odds of this occurring in any specific hand are 0.000005. For more about the combin function, check out my section on it. video poker appendix 5 In Deuces Wild, if I currently hold three deuces, what is my chance of obtaining four deuces on the draw? And what are the odds if I hold two deuces instead? probabilities in poker .
Holding three deuces allows 46 different combinations to draw one additional deuce and another card. There are combin(47,2)=1081 possible ways to choose two cards from the remaining 47 in the deck. Hence, your chances of drawing four deuces with three held is 46/1081 = 4.26% = 1 in roughly 23.5. If you start with two deuces, there are 45 combinations that would yield two more deuces along with a different card. The number of ways to choose three cards from 47 is combin(47,3)=16215. Therefore, the probability of drawing four deuces while holding two is 45/16215 = 0.28% = about 1 in 360.33.
Is it ever advisable to attempt a 'double-up' in video poker?
Definitely. The double up option is among the few bets that carry no house edge. For this reason, I endorse the odds in craps and the double-up feature in video poker. However, if you're engaged in a game with a return exceeding 100%, I would advise against it. Also, if you find that your nerves can't handle the heightened volatility linked to the double up feature, then it's best to avoid it. It's noteworthy that at land-based casinos, cash back is not applicable to double-up bets, while at Playtech online casinos, you receive 0.1% cash back on all bets, including double-ups.
I'm aware that the payout for a full pay Deuces Wild video poker machine stands at 100.76 percent when following the strategies detailed on your site. This is obviously under the assumption of unlimited play. I’m curious to know how many hands one would have to play to achieve that return with a certainty of about 90 percent.
P.S. Where can I find full pay Deuces Wild games in Las Vegas?
There isn't a specific number that guarantees a 90% chance of hitting or exceeding that payout percentage. While the more hands you play, the closer your return approaches 100.76%, it's important to remember that about half the time, it will be above that number and half below. A more relevant question might be how many hands are needed to ensure a 90% chance of reaching at least 100.66%.
The standard deviation for full pay Deuces Wild is estimated at 5.08. The standard deviation of the sample mean is 5.08 divided by the square root of n, where n represents the total number of hands played. Rather than delving into the rest of the computations, I’ll get to the conclusion: it equates to an impressive 42,383,720 hands—quite a lot! If your objective is simply to come out on top with a 90% likelihood, you'd only need to play 733,790 hands. Still, that's a considerable amount of gameplay, underscoring how unpredictable your bankroll can be in the short term. The general formula to find your sample return (at least x) with a probability p uses Excel as (normsinv(1-p)*5.08/(1.0076-x))^2. For my first example, you would enter the following formula in any cell:
This equation can be applied to any game by replacing it with the corresponding standard deviation per hand.
=(NORMSINV(1-0.9)*5.08/(1.0076-1.0066))^2
I believe all Stations and Fiesta casinos offer full pay Deuces Wild in quarter denominations. Green Valley Ranch does too. It was much easier to locate these when I moved to Vegas three years ago.
I think I came across a statement suggesting that if someone devised a system providing just a 1% edge for players, turning $1,000 into $1,000,000 would be relatively straightforward. Yet, in the case of video poker, where the player edge is merely 0.77%, why isn’t wealth multiplying in the same manner? Is it perhaps due to the betting cap of $5 at a time, which significantly prolongs the process? Thank you, and I must say again, I greatly appreciate your site!
Thanks a lot! Yes, as I mentioned earlier, if I had a betting strategy with even a 1% advantage, it could potentially convert $1,000 into $1,000,000 simply by capitalizing on that edge. This concept applies to video poker as well, but the journey would be much longer since the 0.77% advantage version (full pay Deuces Wild) is typically found at the quarter level. Assuming you manage to play 1,000 hands in an hour—an impressive rate hardly anyone achieves—and played flawlessly, you'd likely see an average profit of $9.63 per hour. To reach the $1,000,000 mark would entail nearly 11.86 years of constant play. Moreover, beginning with just $1,000 is quite underfunded for quarter video poker, resulting in a high risk of going bust. It would be considerably faster to attain the $1,000,000 mark with the same advantage in table games since higher bets can be placed.
What are the odds of playing 14,000 hands of Deuces Wild without encountering four deuces?
The chance of drawing four deuces in a single hand is 0.000204. Therefore, the likelihood of not drawing four deuces in any given hand is 1-0.000204 = 0.999796. Consequently, the probability of playing through 14,000 hands without drawing four deuces is equal to 0.999796.
We can see from my deuces wild section Video Poker - Deuces Wild - Wizard of Odds14000= 5.75%.
Find the Top Online Casinos Available in Your Region
Calculator for Estimating Lottery Jackpot Ticket Sales
Participate in Slot Tournaments Offering Huge Prize Pools
I reviewed the anticipated payouts for different deuces wild pay structures, but I couldn't locate the specific schedule I needed. Could you provide me with the expected payout for a deuces wild game that follows this particular schedule: Anything’s Wild I'd attempt this myself, but I don't have the right software since I'm not on Windows.
In full pay deuces wild I observed that in your complete Deuces Wild strategy guide, the payout for one pair (without a deuce) ranks higher than for two pairs. Does this imply that if I draw two pairs, I should opt to discard three cards and retain just one of the pairs? If that’s the case, how do I determine which pair to keep?
Indeed, you should keep just one of the pairs. The only instance where this rule about two pairs can be overlooked is when you also have three cards towards a royal flush. It doesn't matter which pair you decide to keep. This represents one of the rare moments in various skill-based games where the player can have some discretion in strategy. Personally, I like to hold onto the higher pair to avoid wasting time choosing.
What approach should I take for the following hands in deuces wild video poker when both a flush and four of a kind pay out 4 to 1? (1) two pair, (2) a deuce paired with two suited high cards.
I’ll assume that the rest of the payout structure remains the same as before.
| Card Held | Probability on deal | Probability on draw | Total probability |
| 0 | 0.19066396 | 0.0000014 | 0.00000027 |
| 1 | 0 | 0.00000561 | 0 |
| 2 | 0.01969711 | 0.00006167 | 0.00000121 |
| 3 | 0.01299751 | 0.00092507 | 0.00001202 |
| 4 | 0.0003309 | 0.0212766 | 0.00000704 |
| 5 | 0.00000154 | 1 | 0.00000154 |
| Total | 0.22369101 | 0 | 0.00002208 |
In this scenario, (1) keep the two pair, (2) retain the deuce along with both high cards.
Are there any online casinos that feature looser deuces wild games, and which ones provide the best payouts for such games? Thank you.
Atlantic Interbet offers a full pay deuces wild option with a return rate of 100.77%. I believe they allow a maximum bet of 50 cents for this game.
| Card Held | Probability on deal | Probability on draw | Total probability |
| 0 | 0.19066396 | 0.00000698 | 0.00000133 |
| 1 | 0 | 0.00002803 | 0 |
| 2 | 0.01969711 | 0.00030832 | 0.00000607 |
| 3 | 0.01299751 | 0.0046168 | 0.00006001 |
| 4 | 0.0003309 | 0.10195134 | 0.00003374 |
| 5 | 0.00000154 | 1 | 0.00000154 |
| Total | 0.22369101 | 0 | 0.00010268 |
While using your deuces wild video poker software, I was dealt the following cards: QJ8 of spades, T7 of diamonds. I decided to go for the four-card inside straight draw while retaining QJT8. However, the advice feature suggested to keep JT87 and discard the Q. This seems like one of those instances where two different plays could result in the same expected value, similar to when you have two pairs and need to choose just one.5= 0.101951341, which is about 4.79 times as high.
You're correct. There are indeed two viable ways to pursue an inside straight, each yielding the same expected value. I apologize if my program criticized your choice; I should revise that. "optimal\" strategy in Deuces Wild This is a fantastic website, interesting and packed with information. While reviewing the plays for deuces wild video poker, I became confused about the concept of a penalty card. Could you clarify this for me?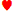 ,
, 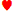 ,
,  ,
,  . In this case everything should be discarded. Now if you get the same hand with an 8d as last card (instead of the 7d),then you should keep the suited Kh and Qh. My question is what difference does it make? Whatever you discard (3c,4d,7
. In this case everything should be discarded. Now if you get the same hand with an 8d as last card (instead of the 7d),then you should keep the suited Kh and Qh. My question is what difference does it make? Whatever you discard (3c,4d,7 or 3c,4
or 3c,4 ,8
,8 ) the odds for getting a royal flush (or straight flush or even anything else) seem the same for me. Since you already have two cards for the Royal Flush why not keep them whatever you have to discard?
) the odds for getting a royal flush (or straight flush or even anything else) seem the same for me. Since you already have two cards for the Royal Flush why not keep them whatever you have to discard?
I appreciate your kind words. I've just revised my explanation regarding penalty cards. In my view, beginner players shouldn't adopt strategies that involve penalty cards. However, for those aiming to play almost flawlessly, here’s my definition: 'A penalty card is a card that, while potentially useful, is discarded. For instance, if a player has three cards towards a royal flush but also has four cards for a flush, the optimal move is to retain the three cards towards the royal and discard the fourth suited card. That discarded card becomes a flush penalty card since it could have contributed to completing a flush; thus, by letting it go, the player's chances of making a flush are "penalized." Sometimes, penalty cards can influence borderline decisions. For example, if a player holds a suited 10 and king, without any other cards from that suit or a 9, jack, queen, or ace, they should keep the two cards toward a royal flush. However, this choice is only marginally superior to discarding everything. If the player holds a single suited card or any cards that could form a straight, the odds of making a flush or straight would be diminished, lowering the overall expected return beneath that of discarding everything. Therefore, players should be attentive to how penalty cards impact their choices.' there are 1,606 ways to make a straight, and with the 8d there are only 1,591. The more spread apart your discards are, the harder it will be to make a straight on the draw. This particular case is very borderline. Those 15 extra ways to make a straight by tossing the 7
there are 1,606 ways to make a straight, and with the 8d there are only 1,591. The more spread apart your discards are, the harder it will be to make a straight on the draw. This particular case is very borderline. Those 15 extra ways to make a straight by tossing the 7 pushes the value of tossing everything over that of keeping two to a royal. For the same reason, in a six-deck game of blackjack you double A2 against a 5 but not a 4. The value of doubling is the same in both cases, but the value of hitting is more against the 4, pushing it above the value of doubling.
pushes the value of tossing everything over that of keeping two to a royal. For the same reason, in a six-deck game of blackjack you double A2 against a 5 but not a 4. The value of doubling is the same in both cases, but the value of hitting is more against the 4, pushing it above the value of doubling.
I went to play deuces wild video poker and noticed quite a varied set of payout odds across different machines. None of those matched the favorable odds you previously analyzed for players. Could it be that casinos have modified the odds after observing your winning tactics? If that’s the case, I really appreciate it, Wizard!
I doubt that I directly influenced the changes, but there’s a case to be made that gambling analysts like myself (especially Bob Dancer) contributed to the degradation of video poker games. Nonetheless, if it weren’t for experts teaching effective strategies, only a select few would know the correct way to play.
I have a rather intriguing computation to explore. While playing Deuces Wild Video Poker, I ended up with an undesirable hand. After discarding all five cards, I drew four deuces, yielding 1,000 coins! What are the odds of drawing four deuces after discarding my original five cards? Thank you for your assistance, and keep up the fantastic work on your site! P.S. While on the same machine, I switched to Deuces Wild Bonus Poker and was dealt three wild cards along with the 4 and 5 of diamonds (creating a straight flush), then discarded the 4 and 5 only to draw four deuces with an Ace, winning 2,000! What a lucky streak I had! This happened at Soboba Casino in Southern California.
No problem. There are combin(47,5)=1533939 different combinations to make 5 cards from the remaining 47 in the deck. Out of those combinations, 43 would give you four deuces (since the fifth card can be any one of the 43 other cards). Hence, the probability of drawing four deuces from the draw is 43/1533939 = 1/35673 = 0.000028032. If you already have three deuces and you draw one more, the odds become (47-1)/combin(47,2) = 46/1081 = 0.0426. In my. VPfree.com you can observe the likelihood distribution in deuces wild concerning how many cards are drawn for any specific hand. For instance, 2.62% of all four deuces will occur through the draw. The chance of this occurring on any single hand is 0.000005. For more detailed insights into the combin function, please refer to my section on.
Given that the odds of a Royal in full pay deuces wild When playing deuces wild, if I have three deuces, what are my chances of drawing a fourth one? What if I only have two?
Holding onto three deuces gives you 46 possible ways to draw the final deuce and another card. The number of ways to select two cards from the 47 remaining in the deck is combin(47,2)=1081. Therefore, your chances of achieving four deuces should you hold three is 46/1081 = 4.26% or approximately 1 in every 23.5 hands. On the contrary, if you possess two deuces, your chances of drawing two more deuces plus another card are 45. The total number of combinations for selecting three cards out of the 47 available is combin(47,3)=16215. Consequently, if you already have two deuces, the probability of acquiring four deuces from the draw drops to 45/16215 = 0.28% which translates to about 1 in 360.33. combin (6000,2)×(1/45282)2×(45281/45282)5998= 0.007688177, or 1 in 130.
Is it ever a smart strategy to attempt a \"double-up\" in video poker?
Absolutely! The double-up feature stands out as one of the few wagers lacking a house edge. As I advocate for odds in craps, I am equally supportive of the double-up option in video poker. Nevertheless, if you’re playing a game with a return exceeding 100%, I would advise against it. Additionally, if you are not prepared to handle the extra volatility introduced by the double-up, it’s best to avoid that option altogether. It's also interesting to note that, in brick-and-mortar casinos, cash-back does not apply to double-up bets, but at Playtech Internet casinos, you earn 0.1% cash back on all bets, including doubles.
I noticed that the rate of return on a full pay deuces wild video poker machine stands at 100.76% with the strategy outlined on your site. This figure is based on continuous play. My question is, how many hands must one play to achieve that return, let's say with a 90% level of confidence?
P.S. Where can I find full pay deuces wild machines in Las Vegas?
There isn’t a definitive number of hands that guarantees a 90% probability of hitting or exceeding that return. While the longer you play, the closer your actual return will align with 100.76%, results will typically fall above or below that mark. Perhaps a more relevant question might be how many hands would one need to play to confidently reach a return of 100.66% with that level of certainty?
The standard deviation for full pay deuces wild sits at 5.08. The standard deviation of the sample mean is calculated as 5.08/sqr(n), where n represents the hands played. I’ll skip over the intricate details of the math and lead to the conclusion: 42,383,720 hands are needed, which is quite a lot! If your aim is to simply break even with a 90% confidence level, you would only need to play 733,790 hands. That is still a substantial number, clearly showing how volatile bankrolls can be over short periods. The general formula used in Excel for determining a sample return of at least x, with a probability of p is (normsinv(1-p)*5.08/(1.0076-x))^2. In the case of my initial example, you would enter the following in any cell: video poker calculator This formula is adaptable for any game by ensuring you substitute in the correct standard deviation for each hand.
I believe all the Stations and Fiesta casinos offer full pay deuces wild, but only in quarter coin denominations. Green Valley Ranch as well. Since relocating to Vegas three years ago, it was noticeably easier to find.
I believe I read somewhere that if someone could devise a system that provided even just a 1% advantage for the player, you could quickly turn $1,000 into $1,000,000. However, some video pokers only give a 0.77% player edge; why aren’t you achieving something like $770,000 instead? Is it because the maximum bet is capped at $5 and escalating winnings would take an impractical amount of time? Thanks! And let me reiterate, I absolutely LOVE your site!! Kelly bet Thank you! As previously mentioned, if I possessed a betting system yielding merely a 1% edge, I could feasibly convert $1,000 into $1,000,000 just by maximizing that advantage. This is likewise achievable in video poker, but it would take considerably longer, given that the 0.77% advantage (in full pay deuces wild) is typically only available at the quarter betting level. Assuming one could average 1,000 hands per hour (a pace that few can realistically maintain) while playing flawlessly, it would yield an average earning of $9.63 per hour. To accumulate $1,000,000 would necessitate nearly 11.86 years of nonstop play. On top of this, starting with just $1,000 would be limited for quarter video poker stakes, thus significantly raising the risk of going bankrupt. It would be quicker to reach the $1,000,000 milestone by finding the same edge in a table game, as higher bets can be used.
What are the chances of playing 14,000 hands of deuces wild and not hitting four deuces? full pay deuces wild Video Poker - Deuces Wild - Wizard of Odds


