Non-Casino Games - FAQ
I enjoy playing a game called liars poker using dollar bills. What are the chances of drawing 1, 2, 3, 4, or 5 of the same number on a bill? Thank you. Also, if I'm playing with 3 people, what's the likelihood of any one number appearing?
To begin with, let me address the unspoken query regarding how often a particular digit can appear n times on a randomly drawn bill. Since each bill contains 8 digits, the formula for the occurrence of n of a specific digit is combin(8,n) multiplied by 0.1.n*0.98-n/108The following table outlines the probabilities ranging from 0 to 8 occurrences of a chosen digit.
Specific Number Odds in Liar's Poker
| Number | Probability |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Total | 1.00000000 |
The subsequent table illustrates the chances associated with different types of bills, sorted by the number of n-of-a-kind. For instance, a serial number like 66847680 possesses one triplet, one pair, and three unique digits, translating to a probability of 0.1693440.
General Probabilities in Liar's Poker
| 8 o.a.k. | 7 o.a.k. | 6 o.a.k. | 5 o.a.k. | 4 o.a.k. | 3 o.a.k. | 2 o.a.k. | 1 o.a.k. | Probability |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Total | 1.0000000 | |||||||
o.a.k. = 'of a kind'
For more information, see my page on liars poker .
Bank of America is hosting a contest where a selected deposit made at an ATM is tripled. This contest will run for approximately two months. Should I make three separate deposits of $100 or just one deposit of $300 to improve my chances? Or is the difference negligible considering the overall odds?
Your potential winnings remain the same, regardless of whether you split your total deposits into multiple parts or not. A sound strategy would be to repeatedly deposit and withdraw the same amount as often as possible. Nevertheless, if the odds are particularly unfavorable, you might find it isn't worth the hassle.
I have a question concerning an Asian dice game where players bet on which number from 1 to 6 will appear. Players place their wagers like they do in roulette, and then the dealer rolls three dice at once. If a chosen number appears once, payouts are at 1:1; if it appears twice, it's 2:1; and if it shows up on all three dice, the payout is 3:1. What do you think would be the ideal number of bets to place, assuming all bets are of equal value?
The probability of rolling three matching numbers is 1/216. For two matching numbers, it's 3*5/216. One match has a probability of 25*5/216, while rolling zero matches stands at 5*5*5/216. Therefore, the expected return can be calculated as 3*(1/216) + 2*(15/216) + 1*(75/216) - 1*(125/216) = -17/216 = -7.87%. There is no best number of bets to place, as you will always expect to lose approximately 7.87% of your total bets, no matter what strategy you employ.
These bets can be made in both sic bo and chuck a luck .
What are the chances of winning a standard game of Klondike Solitaire, especially the version in Windows?
This is a question I receive quite frequently, but unfortunately, I don't have a definitive answer. An exhaustive study of Klondike Solitaire has never been undertaken. Perhaps in the distant future when computers are significantly faster, someone will finally accomplish this. However, it's been said that Las Vegas casinos offered Klondike at least back in the 1950s. I've inquired with various Vegas veterans for confirmation, but none have verified it yet.
During a recent game of backgammon, I rolled double sixes four times in a row. What are the odds of that occurrence happening again?
With each new roll, the chance that the next four rolls will all result in double sixes is 1/36.4= 1 in 1679616.
Hi, at www.transience.com.au/pearl.html There’s a game called Pearls for Swine where pearls are arranged in three rows (5+4+3) and on your turn, you can remove any number of pearls from a single row. The goal is to leave the final pearl or pearls for your opponent to take. I always start the game, yet I end up losing every time. What’s the secret that enables my opponent to win consistently?
To ensure victory, start by removing two pearls from the row containing three, which will leave the configuration as 1+4+5. No matter how your opponent responds, in your next turn, position the game to leave them with one of these combinations: 1+1+1, 1+2+3, or 4+4. This strategy will allow you to force your opponent into a situation with two piles of two or more or an odd number of one-pile configurations.
What set in monopoly is the best?
My favorite color set is orange because it yields the highest return on investment. For instance, owning a hotel on the orange set costs $500, while the average rent from it is $966.67, giving a rent to cost ratio of 1.93. The only set with a better ratio is the light blue set, which stands at 2.27. Nevertheless, the maximum rent from the light blues is only $600. With three houses on the orange properties, the rent equals the hotel rents on the light blue properties, but they cost 20% less and allow for further development. Plus, oranges are frequently landed on after just being released from jail. Thus, I advise you to prioritize acquiring the orange set when trading.
What tips do you have for playing rock/paper/scissors?
Perhaps the most valuable advice on this site is to always begin with paper in the first round. This is based on the tendency of novice players to select rock initially. If you extend your hand to form each gesture one after the other, you’ll notice that rock feels the most natural and instinctual. In repeated rounds, you might choose the option that counters whatever your opponent played in the previous round with a probability of less than one-third, as I believe newbies rarely repeat their choices more than a third of the time. If you're up against an experienced opponent who may read your mind, randomize your choices by looking at the second hand of your watch, dividing the number of seconds by three, and using the remainder to determine your move: 0 for rock, 1 for scissors, and 2 for paper (or any other predetermined mapping). Therefore, at your next meal split check decision, I suggest you place a single round bet and start with paper. I look forward to you sharing your gratitude after.
Who holds the upper hand in Risk when the attacker uses three dice against the defender's two?
For those who might not be acquainted with it, Risk is considered one of the best board games ever created. If you haven't played it, you have yet to experience life. In typical gameplay, where a battle scenario includes three attacking versus two defending dice, there are various outcomes to consider.
- Defender loses both: 37.17%
- Each loses one: 33.58%
- Attacker loses both: 29.26%
In the game of Yahtzee, if the only thing remaining on your scorecard is the Yahtzee itself, what are the chances of achieving that?
The next table details the chances of successfully rolling a Yahtzee on your final roll, depending on how many additional dice you require.
Last Roll Yahtzee Probabilities
| Needed | Probability of Success |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
The subsequent table lists the probabilities for various improvements. The left column indicates how many more dice are needed before any roll, while the top row shows how many are required after rolling. The table body reveals the likelihood of achieving the specified improvement.
Probabilities of Improvement
| Need Before Roll | 0 | 1 | 2 | 3 | 4 | Total |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
The following table displays the probabilities regarding the initial roll where you may need anywhere from 0 to 4 additional dice to obtain a Yahtzee.
First Roll Yahtzee Probabilities
| Needed | Probability |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
The next table outlines the probabilities of enhancement leading to eventual success based on the number of additional dice you'll need after the first roll. For instance, if a player requires three additional dice to make a Yahtzee, the chance of improving to needing two more after the second roll and achieving the Yahtzee on the third roll is 0.010288066.
The probabilities related to achieving a Yahtzee after the first roll, according to how many dice are needed before and after the second roll.
| Need Before Roll | 0 | 1 | 2 | 3 | 4 | Total |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
To arrive at the final answer, multiply the probability from the earlier table of needing a specific number of dice after the first roll by the probability of eventual success found in the last column of the previous table. This yields 0.092593*0.012631 + 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643%. To validate this, I conducted a simulation of 100 million games and the simulated probability came to 4.60562%.
If we introduce dynamite as an alternative in rock/paper/scissors, where dynamite defeats both rock and paper, but is overcome by scissors, what optimal strategy should two perfectly logical players employ against each other?
Initially, it's clear that you should never choose paper. Regardless of what your opponent throws, opting for dynamite will yield equal or better odds than selecting paper. When paper is no longer an option, dynamite effectively replaces it as it beats rock and falls to scissors. Thus, the best approach is to randomly and equally choose between rock, scissors, and dynamite.
What techniques yield the best results in those booths where cash flutters around, and you must gather as much as possible within a strict time limit?
I posed this inquiry to Randy Hill, who said that a winning strategy is to extend your arms out straight with palms facing down, allowing the money to blow against your hands and arms. Once sufficient has gathered, push it through the slot to collect your winnings. Fun Industries Inc. Imagine we have a gambling scenario involving a fair coin flipped multiple times. You must pay 1 rupee for every flip, and the outcomes can either be heads or tails. If the difference between heads and tails reaches 3, you will earn 8 rupees. Should we engage in this game, and why? How do we calculate our chances of winning? Additionally, how would the winning probability change if we were to receive 7 or 9 rupees?
Let’s denote x as the expected amount of flips from the starting point.
We can designate y as the expected flips remaining when one side is slightly ahead by one flip.
We will call z the expected number of flips left if one side leads by two flips.
Using straightforward matrix algebra, we can determine that E(x) = 9, E(y) = 8, and E(z) = 5. Hence, it would take approximately 9 flips for the difference between heads and tails to reach 3. At a payout of 8 rupees, this presents a viable wager for the individual collecting 1 rupee per flip, as they can expect to receive 9 rupees on average while only paying back 8. The gambler's house edge stands at 11.11%. At a payout of 9 rupees, the bet breaks even, while at 7 rupees, the house advantage increases to 22.22%.
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
You referenced the appropriate tactics for approaching the game.
In your Nov 28, 2002 In the column dated 11/28/02, I outlined gameplay strategy for scenarios where only three rows remain. Now, here’s my approach for managing four rows. When taking your turn, reference the left column for the configuration and execute the corresponding action from the right column. For example, with a starting configuration of 3456, as indicated last, you should take away 4 pearls from the row of 5, resulting in a configuration of 1346. If the left column indicates 'Lose,' you'll find it impossible to win if your opponent employs optimal strategy, which they do consistently in the game at Transcience. Pearls Before Swine . They also have a sequel called Pearls Before Swine II . How do I beat this version?
Non-Gambling Game Insights - Common Questions - Wizard of Odds
Find the Top Online Casinos Available in Your Region
Pearls Before Swine II Strategy
| You Have | Leave |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | Lose |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | Lose |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | Lose |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | Lose |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | Lose |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | Lose |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | Lose |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | Lose |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | Lose |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | Lose |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | Lose |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | Lose |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | Lose |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | 3 = 2+1 |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Calculator for Lottery Jackpot Ticket Sales
- 4 = 4
- 5 = 4+1
- 6 = 4+2
- Try this strategy on the
Enter into exciting slot tournaments that boast huge prize pools
Pearl 3 Je ne pas compre your I enjoy playing liars poker using dollar bills. Can you help me understand the odds of rolling 1, 2, 3, 4, or 5 of the same number on a bill? Additionally, if I'm playing with three participants, what are the chances of any single number appearing?
NIM Needed To begin with, I will clarify an important aspect regarding the likelihood of a certain number appearing n times on a random bill. Since there are eight digits on a bill, the chance of n occurrences of a specific digit can be calculated with the formula combin(8,n)*0.1.
Below, you will find a table that displays the probabilities for seeing between 0 and 8 instances of a specific digit.
The following table illustrates the probability of each possible bill type, arranged by the count of each n-of-a-kind combination. For instance, the serial number 66847680 features one set of three identical digits, one pair, and three unique digits, resulting in a probability of 0.1693440.
General Statistics in Liar's Poker
of Success
| Probabilities of Improvement | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Need Before Roll | 3 | 1 | 3 | 2 | 1 |
Bank of America is currently running a promotion that triples certain deposits made at ATMs. This contest will last approximately two months. Should I deposit $300 as a single transaction or split it into three deposits of $100 each? Or are the odds so minimal that dividing the deposit is not worthwhile?
Total
| First Roll Yahtzee Probabilities | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Needed | 2 | 2 | 4 | 2 | 0 |
Your potential winnings remain unchanged irrespective of how you partition your deposits. A wise tactic would involve repeatedly depositing and withdrawing the same amount as often as feasible. However, if the odds are as poor as anticipated, it may not be worth the hassle.
Probability
Need Before Roll
| Total | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| anonymous | 2 | 3 | 3 | 2 | 0 |
I have a question regarding an Asian dice game where players predict which face will land up after a roll. Participants place bets on numbers 1 to 6 (similar to roulette), and then the dealer rolls three dice at once. If your number appears once on any die, the payout is 1:1; twice, it’s 2:1; and if it appears on all three, the payout is 3:1. Given that players can bet as much as they want, what would be the best number of bets to make, assuming each bet is of equal value?
anonymous
| Fun Industries Inc. | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Utpal from Lucknow | 2 | 2 | 2 | 2 | 0 |
Your potential winnings remain unchanged irrespective of how you partition your deposits. A wise tactic would involve repeatedly depositing and withdrawing the same amount as often as feasible. However, if the odds are as poor as anticipated, it may not be worth the hassle.
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
| E(z) = 1 + 0.5*E(y) | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| In your | 1 | 2 | 3 | 1 | 0 |
The chance of all three dice matching is 1/216. The likelihood of two matching is calculated as 3*5/216. If just one matches, the probability is 25*5/216. If none match, it’s 5*5*5/216. Hence, the expected return is computed as 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87%. There is no perfect strategy for the number of bets you should place; you are likely to lose an expected 7.87% of the total money wagered regardless of your actions.
Nov 28, 2002
| Pearls Before Swine | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| . They also have a sequel called | 2 | 2 | 4 | 0 | 0 |
Your potential winnings remain unchanged irrespective of how you partition your deposits. A wise tactic would involve repeatedly depositing and withdrawing the same amount as often as feasible. However, if the odds are as poor as anticipated, it may not be worth the hassle.
Pearls Before Swine II
. How do I beat this version?
| anonymous | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Pearls Before Swine II Strategy | 2 | 3 | 3 | 0 | 0 |
You Have
Leave
| Lose | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Lose | 2 | 2 | 2 | 0 | 0 |
Your potential winnings remain unchanged irrespective of how you partition your deposits. A wise tactic would involve repeatedly depositing and withdrawing the same amount as often as feasible. However, if the odds are as poor as anticipated, it may not be worth the hassle.
Lose
Lose
| Lose | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Lose | 2 | 3 | 1 | 0 | 0 |
What are the chances of winning a classic game of Klondike Solitaire as seen in the Windows version?
Lose
| Lose | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Lose | 2 | 4 | 0 | 0 | 0 |
This is one of the most common inquiries I receive, and unfortunately, I don't have a definitive answer. A comprehensive analysis of Klondike Solitaire has yet to be accomplished. Perhaps in the future, with advancements in computing speed, someone may take on this task. It's said that Las Vegas casinos used to offer the game back in the 1950s, but despite my inquiries to some older Vegas players, none have been able to confirm this.

Recently, during a game of backgammon, I rolled double sixes four times in a row. What are the chances of this occurring again?
Each time you roll, the probability that the next four rolls will again yield double sixes stands at (1/36).

There's a game known as Pearls for Swine where pearls are arranged in three rows (5+4+3). During your turn, you can take any number of pearls from a single row. The goal is to leave the last pearls for your adversary. As the first player (and invariably the loser), can you explain why I consistently fail? My opponent seems to employ a clever strategy that guarantees his victory—could you reveal this tactic?

Lose
To start, remove 2 pearls from the row containing 3 pearls, resulting in a configuration of 1+4+5. Regardless of what your opponent does next, you can guide him to end up with one of these setups: 1+1+1, 1+2+3, or 4+4. From any of these arrangements, maneuver your opponent into a condition where he faces two piles with two or more pearls each or an odd number of singleton piles.
I find the orange property set to be the most appealing due to its strong return on investment. For instance, a hotel on the orange set costs $500, while the average rent is $966.67, resulting in a rent-to-expense ratio of 1.93. The only set with a more favorable ratio is the light blue set, which has a ratio of 2.27; however, its maximum rent caps at only $600. Notably, the rent for three houses on the orange set matches that of light blue hotels but incurs 20% less cost and allows for further development. The orange spaces are also strategically advantageous for landing just after being released from jail. Thus, my suggestion is to prioritize acquiring the orange set when trading.
What would you recommend for playing rock/paper/scissors?
The most valuable piece of advice on this site may be to always choose paper during the first round. This is because inexperienced players typically opt for rock initially. Just extend your hand in each of the three positions and you'll notice that rock tends to be the easiest and most natural selection. In subsequent rounds, select whatever would beat your opponent's last move with a probability of less than a third since amateurs tend to repeat patterns less frequently than that. If you're facing a skilled player who might outsmart you, consider randomizing your choices by observing the seconds hand of your watch, dividing the seconds by three, and using the remainder (0=rock, 1=scissors, 2=paper) to determine your throw. So next time you’re at a restaurant splitting the bill, I suggest playing a quick round for it and starting with paper. You'll owe me one for that!
In the game of Risk, who holds the upper hand when the attacker uses three dice and the defender two?
For those who might not be acquainted with it, Risk is an exceptional board game that everyone should experience. Now, addressing your question concerning the common 3 versus 2 situation, here are the possible outcomes:
In Yahtzee, if the only score remaining on the card is for the Yahtzee itself, what are the chances of achieving it?
The table below depicts the probability of succeeding on the final roll depending on how many additional dice you require to complete a Yahtzee.
The following table illustrates the probabilities of improving your position. The left column indicates how many dice you need before making any given roll, while the top row specifies how many you might need afterward. The body of the table then reveals the probability of varying degrees of improvement.
Another table presents the likelihood of needing from 0 to 4 additional dice to form a Yahtzee based on your first roll.
3 = 2+1
| 4 = 4 | 5 = 4+1 | 6 = 4+2 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| Try this strategy on the | 82600000 | 1 |
The next table outlines the probabilities for improvement followed by eventual success based on the number of dice required after the initial roll. For example, if you still need 3 more dice to complete a Yahtzee, the chance of reducing this requirement to needing just 2 more after the second roll, and then achieving the Yahtzee on your third roll, is 0.010288066.
Probabilities of achieving a Yahtzee following the first roll, considering how many dice are required before and after the second roll.
Je ne pas compre your To derive the final answer, compute the dot product of the number of dice needed after the first roll (from the table two rows above) and the likelihood of eventually succeeding (from the final column of the above table). This results in 0.092593*0.012631 + 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643%. To verify this, I conducted a simulation involving 100 million games, yielding a simulated probability of 4.60562%.
NIM If dynamite is added as a new option in a game of rock/paper/scissors, where dynamite defeats rock and paper but loses to scissors, what would be the advisable approach for two expert logicians playing this game?
Needed Initially, we can eliminate the choice of paper entirely. Regardless of what the opponent plays, selecting dynamite over paper will yield equal or superior results. Once paper is dismissed, dynamite effectively becomes the new version of paper—winning against rock but losing to scissors. Therefore, the optimal strategy is to randomly choose between rock, scissors, and dynamite with equal probability.
Probability What is the most effective strategy in those booths where money gets blown around and you must gather as much as possible within a limited timeframe?
of Success Probabilities of Improvement I posed this question to Randy Hill from [source]. He suggested extending your arms straight out, palms facing down, to catch the cash that swirls up against your hands and arms. When you've gathered a sufficient amount, simply push it through the collection slot. Need Before Roll Imagine we are participating in a gambling game involving a fair coin being flipped repeatedly. Each flip costs us 1 rupee. The outcomes are either heads (H) or tails (T). If the difference between heads and tails reaches 3, we will win 8 rupees from the gambler. Should we participate in this game, and why? What is our probability of winning? Additionally, how does changing the winning amount to 7 or 9 rupees affect our chances?
Let's denote x as the expected number of flips starting from the beginning.
We can define y as the expected number of flips remaining when one outcome reaches a majority by one flip.
| First Roll Yahtzee Probabilities | Needed | Probability | Need Before Roll | Total |
| 0.05 | anonymous | 20.59% | 37.55% | 41.85% |
| 0.10 | anonymous | 20.59% | 37.55% | 41.86% |
| 0.15 | Fun Industries Inc. | 20.57% | 37.55% | 41.87% |
| 0.20 | Utpal from Lucknow | 20.55% | 37.55% | 41.9% |
| 0.25 | E(x) = 1 + E(y) | 20.5% | 37.56% | 41.94% |
| 0.30 | E(y) = 1 + 0.5*E(x) + 0.5*E(z) | 20.43% | 37.56% | 42.01% |
| 0.35 | E(z) = 1 + 0.5*E(y) | 20.33% | 37.58% | 42.10% |
| 0.40 | In your | 20.18% | 37.60% | 42.22% |
| 0.45 | Nov 28, 2002 | 19.97% | 37.64% | 42.39% |
| 0.50 | Pearls Before Swine | 19.68% | 37.71% | 42.61% |
| 0.55 | . They also have a sequel called | 19.26% | 37.81% | 42.93% |
| 0.60 | Pearls Before Swine II | 18.67% | 37.96% | 43.36% |
| 0.65 | . How do I beat this version? | 17.86% | 38.21% | 43.93% |
| 0.70 | anonymous | 21.56% | 38.28% | 40.16% |
| 0.75 | Pearls Before Swine II Strategy | 28.42% | 35.21% | 36.38% |
| 0.80 | You Have | 36.82% | 31.26% | 31.92% |
| 0.85 | Leave | 46.99% | 26.35% | 26.66% |
| 0.90 | Lose | 59.17% | 20.36% | 20.47% |
| 0.95 | Lose | 73.61% | 13.19% | 13.21% |
| 1.00 | Lose | 90.57% | 4.72% | 4.72% |
| Lose | 30.82% | 32.96% | 36.22% |
Then, z will represent the expected number of flips left if one outcome is ahead by two flips.6Lose
LoseLose
Lose
Lose Lose Using matrix algebra, it becomes straightforward to see that E(x) = 9, E(y) = 8, and E(z) = 5. Thus, on average, it takes 9 flips for the difference between heads and tails to reach 3. This means that at 8 rupees, it is a favorable bet for the person collecting 1 rupee per flip, as they will, on average, earn 9 rupees while only paying 8. The house's edge for the gambler stands at 11.11%. If the reward is at 9 rupees, it amounts to a fair wager, while at 7 it increases the house advantage to 22.22%.
In your column, you discussed the correct strategy for this game.
In my column dated 11/28/02, I explain how to approach the game when only three rows remain. Here’s my advice for scenarios with four rows: during your turn, refer to the configuration in the left column and execute the move indicated in the right column. For example, the starting position of 3456 appears at the bottom, suggesting you should remove 4 pearls from the row containing 5, altering it to 1346. If the left column indicates 'Lose,' it means there's no winning way if your opponent plays optimally, which seems to occur consistently at Transcience.
Find the Top Online Casinos Available in Your Region
Calculator for Lottery Jackpot Ticket Sales
Participate in Slot tournaments featuring impressive prize pools
I enjoy engaging in the game called liar's poker using dollar bills. Could you inform me about the chances of rolling any combination of 1, 2, 3, 4, or 5 bills that show the same number? Also, when playing with three participants, what are the odds of a specific number appearing?
| Try this strategy on the | Pearl 3 | Je ne pas compre your | NIM | Jack from Troy | Player’s Turn 1 |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
To address the unasked question regarding the probability of a certain number appearing 'n' times on a randomly chosen bill, there are 8 possible digits on the bill, so the probability for 'n' occurrences of a specific number is calculated as combin(8,n)*0.1.
The table below illustrates the likelihood of obtaining anywhere from 0 to 8 of a specific number. Row Total
The following table illustrates the probabilities of encountering every potential type of bill categorized by occurrences of each specific number. For instance, the serial number 66847680 would have one occurrence of three of a kind, one pair, and three single numbers, which results in a combined probability of 0.1693440.
Computer’s Turn 1 Row Bank of America is currently running a promotion to triple a chosen deposit made at an ATM over a two-month period. Should I go for three deposits of $100 or just one larger deposit of $300? Or, are my overall chances so low that the method I choose won’t really matter?
Your expected winnings remain the same, no matter how you decide to split your deposits. An effective tactic might be to repeatedly deposit and withdraw the same funds. However, it’s possible that the odds are so unfavorable that it may not be worth the effort. Total Here is the binary breakdown of that.2Player’s Turn 226Row
I have a query about an Asian dice game where participants need to predict the outcome on the rolled dice. Players place their bets on the numbers 1 through 6 (similar to roulette), and then the dealer rolls three dice at once. The payouts are as follows: 1:1 if the chosen number appears once, 2:1 for twice, and 3:1 if it appears on all three dice. Given that players can place multiple bets, what is the ideal number of bets to make? (Assuming all bets are the same size)
The odds of rolling three of a kind is 1/216. The odds of rolling two matching numbers is 3*5/216. The odds of rolling one matching number is 25*5/216, while the odds of rolling no matches is 5*5*5/216. Therefore, the expected payout would be calculated as 3*(1/216) + 2*(15/216) + 1*(75/216) - 1*(125/216) = -17/216, equating to -7.87%. There is no ideal number of bets because you can expect to lose around 7.87% of the total money wagered no matter what strategy you use.5What are the chances of winning a regular game of Klondike Solitaire as seen in the Windows version?5This is perhaps the most common inquiry I receive, to which I unfortunately don’t have a concrete answer. A thorough analysis of Klondike Solitaire has yet to be completed. Perhaps in the future, when computers become significantly more powerful, someone will undertake this task. However, it is said that Las Vegas casinos used to feature the game at least back in the 1950s. I have reached out to several longtime Vegas residents for confirmation, but none have succeeded so far.
Just recently, during a backgammon match, I rolled double sixes four times in a row. What are the odds of that happening again?
Each time you roll, the likelihood of getting four consecutive double sixes is (1/36).
| Row | Total | Now we need to change the 1, 4, and 8 columns. |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| Player’s Turn 3 | 635013559600 | 1 |
Begin by taking 2 pearls from the row of 3, resulting in a configuration of 1+4+5. No matter how your opponent responds, on your following turn, ensure to leave them with one of the following setups: 1+1+1, 1+2+3, or 4+4. From any of these positions, you can force your opponent into a situation where they face two piles of 2 or more each, or an odd quantity of piles with 1 each.
I prefer the orange set since it yields the highest return on investment. For instance, a hotel on the orange set requires $500 and the average rent is $966.67, resulting in a rent-to-expense ratio of 1.93. The only set with a better ratio is the light blue set, which has a ratio of 2.27. However, the maximum rent for the light blues is only $600. The rents on the oranges with three houses are comparable to the rents on the light blues at the hotel level, but they cost 20% less, allowing further construction. Additionally, landing on the orange set is favorable right after exiting jail. Therefore, my recommendation is to prioritize acquiring the orange set during trades.
Total
| Computer’s Turn 3 | Row | Total | Now we need to change the 2 and 4 totals. |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18.00 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12.00 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | Player’s Turn 4 |
| 0.09 | 8.00 | 8.04 | Row |
| 0.10 | 7.20 | 7.27 | Total |
| 0.11 | 6.55 | 6.64 | This can be done by changing the 6 to a 0. |
| 0.12 | 6.00 | 6.12 | Computer’s Turn 4 |
| 0.13 | 5.54 | 5.67 | Row |
| 0.14 | 5.14 | 5.29 | Total |
| 0.15 | 4.80 | 4.96 | Now we need to change the 2s and 4s. |
| 0.16 | 4.50 | 4.67 | Player’s Turn 5 |
| 0.17 | 4.24 | 4.41 | Row |
| 0.18 | 4.00 | 4.19 | Total |
| 0.19 | 3.79 | 3.98 | Computer’s Turn 5 |
| 0.20 | 3.60 | 3.80 | Row |
What strategies do you suggest for playing rock/paper/scissors?
TotalHere is the end of the game.
Mike from OlympiaTom from Buffalo, NY
Ian F. from Provo
Yahtzee Experiment
One of the best pieces of advice I can offer from this site is this: In the first round, ALWAYS CHOOSE PAPER. This is based on the fact that inexperienced players typically opt for rock during the first throw. By extending your hand for each selection, you’ll notice that rock feels like the most intuitive choice. For subsequent rounds, select the option that would counter whatever your opponent played in the previous round, knowing that they will likely repeat less frequently than one-third of the time. If you find yourself competing against a professional who may be able to read your strategy, an effective technique is to randomize your choices. For instance, glance at the second hand of your watch, divide the seconds by three, and use the remainder for your choice—0 for rock, 1 for scissors, and 2 for paper (as long as you have predetermined your mapping). During your next visit to a restaurant where you split the bill, consider playing a single round for the check and start with paper. You can thank me later.
Rolls
1/x = x at values of x close to 1.
So the dy/dx = 1 for values of x close to 1.
In the game of Risk, who has the upper hand when the attacker rolls three dice against the defender’s two?
For those who are not aware, Risk is an iconic board game celebrated by many. If you haven't experienced it, you haven't truly lived. Regarding your question about a standard 3-on-2 battle, here are the possible outcomes:
The "rule of 72" is saying that .72/i = .6931/ln(1+i).
In Yahtzee, if only the Yahtzee itself remains on your scorecard, what is the probability of achieving it?
The table below provides the likelihood of achieving success on the final roll based on how many additional dice you need to complete a Yahtzee.
The next table shows the probabilities of enhancing your situation. The left column indicates how many dice you need prior to any given roll, while the top row outlines how many you still require after that roll. The main body presents the probabilities of various levels of improvement.
The subsequent table addresses the probabilities on the initial roll for needing anywhere from 0 to 4 more dice to secure a Yahtzee.
Another table illustrates the probabilities of improving your situation and ultimately achieving success based on how many additional dice are needed after the first roll. For instance, if a player needs three more dice to achieve a Yahtzee, the chances of reducing that to needing two after the second roll and then making the Yahtzee on the third roll is approximately 0.010288066. Occurrences .
Probabilities for securing a Yahtzee following the first roll, based on the number of required dice before and after the second roll.
To finalize the calculation, take the dot product of the required dice count following the first roll (from the table two tables above) and the probability of eventual success in the last column of the preceding table. This results in 0.092593*0.012631 + 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643%. I verified this finding with a simulation of 100,000,000 games, yielding a simulated probability of 4.60562%.
If dynamite is introduced as a third option in the rock/paper/scissors game, where dynamite defeats both rock and paper while scissors counters dynamite, what should be the optimal strategy if two ideal logicians are playing?
To start, it’s clear that playing paper should never be an option. No matter the opponent's throw, you will come out on equal or even better terms by throwing dynamite instead. Once paper is excluded, dynamite effectively takes on the role of paper, defeating rock while losing to scissors. Consequently, the best strategy would be to randomly choose between rock, scissors, and dynamite with equal probability. How can one maximize their success in those booths where money is blown about, and you have a limited time to collect as much as possible? I posed this question to Randy Hill from [source]. He suggested that you should extend your arms straight out, palms facing down, allowing the money to accumulate against your hands and arms as it blows around. Once you've gathered a sufficient amount, you can then push it through the slot.
- Imagine we have a gambling scenario involving an unbiased coin flipped several times. Each coin flip requires a payment of 1 rupee. The outcome can either be H (heads) or T (tails). If the difference between the number of heads and tails reaches 3, we would receive 8 rupees from the gambler. Should we engage in this game, and why? What are the chances of winning? How would the probabilities shift if we were to receive either 7 or 9 rupees?
- Let’s denote x as the anticipated number of flips from the starting point.
- We’ll use y to represent the expected number of flips remaining if one side is ahead by one flip.
- Let z denote the expected number of flips remaining if one side leads by two flips.
Total
Tony Backgammon
501 Essential Backgammon ProblemsSnowie backgammon software 1 11 0.076923 2 19 0.132867 3 39 0.272727 4 44 0.307692 5 19 0.132867 6 11 0.076923 Motif website 143 1.000000 - It becomes straightforward matrix algebra to establish that E(x) = 9, E(y) = 8, and E(z) = 5. Thus, on average, one would need 9 flips to achieve a difference of 3 between heads and tails. Therefore, at 8 rupees, it represents a favorable bet for the player, as they would expect to garner about 9 rupees while only paying 8. The house edge for the gambler is calculated to be 11.11%. With a payout of 9 rupees, it becomes an even bet, while at 7 rupees, the house advantage increases to 22.22%.
In the
April 11, 2004 column Showcase Showdown
Mike P.8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 Spin 1 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - In your writing, you addressed the ideal strategy for the game.
In my article dated 11/28/02, I elaborate on how to play when only three rows are left. Here’s my recommended approach for scenarios with four rows. When it is your turn, refer to the configuration on the left column and play accordingly from the right column. For example, if you begin with the configuration 3456, it corresponds to the last entry which suggests taking 4 pearls from the row of 5, leaving a configuration of 1346. If the left column indicates 'Lose', it means there is no winning strategy available if your opponent plays optimally, which seems to be a common trait of the game at Transcience.
In this table, a strategic approach seems to be directing your opponent into a scenario where the total number of pearls in the row with the least and most pearls matches the count in the two central rows. This strategy might involve ensuring the row with the least pearls has none at all.
Brad S. contributed a broader tactic that can be applied, regardless of the count of pearls and rows involved. Initially, analyze each row into its binary segments. For instance, in the game of Transcience, the initial setup can be depicted as follows.
Strategy
| Player 1 | Player 2 | Player 3 spin |
spin spin spin |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0.00000000005 | 100 | 0.00000000464 |
| spin | 1.00000000000 | 0 | 0.01961648451 |
Subsequently, one should aim to maintain an even quantity of each power of 2. In the previously mentioned scenario, for example, there are doubles of 1’s and 2’s and triplicates of 4’s. This creates an excess of 4. You would then subtract 4 from any row containing a 4. Continue this process until your opponent is left facing either a pair of 2’s or an odd number of 1's.
spin
| spin | spin |
| spin | 0.0028 |
| spin | 0.0196 |
| Once you're familiar with this gameplay, it guarantees victory every time. However, if you begin from a disadvantageous setup, like in my 10th game (4+7+8+11), you can opt to press 'go' to let your opponent take the first shot. | 6.9698 |
| spin | 5238.7950 |
| spin | 559.9874 |
| spin | 560.9874 |
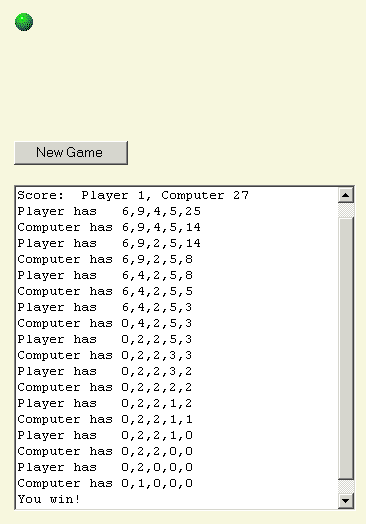
In this game, I often believed that winning hinged on leaving the opponent—here, the computer—with a number of dots that correspond to the immediate lower integer, aligning with its binary sum. For instance, if I have 17 dots, I would take away 2 to leave 15, which aligns with the binary totals of 1, 2, 4, and 8. Yet this approach doesn't seem to work effectively. Is my reasoning sound or flawed?168While you're on a promising path regarding the binary breakdown, that’s not entirely the key to winning. Ideally, aim to hand your opponent an odd count of rows, each with just one pearl. If that's impossible, proceed to deconstruct each row into its binary elements. Take the number 99 as an example, which can be expressed as 64+32+2+1. Next, tally the instances of each binary component across all rows. Finally, identify a move that results in the opponent having an even count of all binary elements. stay ).
Let's consider a practical example. Assume it's your turn with the following arrangement.
stay
Notice that there are odd counts of 1s, 2s, 4s, and 16s. It's evident we need to reduce the row with 25 down to 16 to eliminate that 16 component. In order to keep the binary totals even, we should remove a 1, introduce a 2, add a 4, hold onto the 8, and eliminate the 16. Thus, the optimal move is to take out 2, 4, and 8, totaling 14 from the last row, which leaves us with the following.
After the computer makes its move, we are left in this position. stay At this point, we need to remove a 2 and a 4 to achieve even totals. The single row hosting both components is the 14, so we subtract 6 from there, resulting in 8.
Another table illustrates the probabilities of improving your situation and ultimately achieving success based on how many additional dice are needed after the first roll. For instance, if a player needs three more dice to achieve a Yahtzee, the chances of reducing that to needing two after the second roll and then making the Yahtzee on the third roll is approximately 0.010288066. Average .
This can be adjusted by altering the 8 to 5, as demonstrated.
This change can be made by adjusting the 5 to a 3. If you can maneuver your opponent into a situation where rows are structured as x,x,y,y, your chances of winning become significantly increased, assuming you maintain this condition until the end.
- In subsequent turns, I ensure the computer remains engaged in x,x,y,y configurations. In this instance, the computer presents me with 2,2,3,2; hence, I reset it to 2,2,2,2.
- Next, the computer gives me 2,2,1,2. I adjust it again to 2,2,1,1.
- The sequence continues with the computer giving me 2,2,1. I further reduce it to 2,2. Achieving two equal rows for your opponent virtually guarantees your win, provided you maintain their equality.
- Eventually, the computer leaves me with a solo pile of 2, to which I remove 1.
I recently came into possession of a carnival wheel passed down from my great uncle. It's a century old and features numbers from 1 to 60 in a random arrangement, alternating between black and red, while showcasing a green star every fifteenth number. I could use your expertise to help me determine the appropriate payouts for each spin.
Thus, there are 30 black numbers, 30 red numbers, alongside 4 green ones, giving us probabilities of 30 out of 64 for black, 30 out of 64 for red, and 4 out of 64 for green. The fair odds calculation for an event with probability p is (1-p)/p to 1. Therefore, for red, the fair odds equate to (34/64)/(30/64) = 34 to 30, simplifying down to 17 to 15. The same applies to black. As for green, the fair odds amount to (60/64)/(4/64) = 60 to 4, translating to 15 to 1. When it comes to a specific number, the fair odds are (63/64)/(1/64), equating to 63 to 1.
I would recommend paying 1 to 1 on red and black bets, providing odds of 14 to 1 on green, and offering 60 to 1 on each individual number. In terms of the house edge, a formula would be (t-a)/(t+1), where t signifies true odds and a represents actual odds. Consequently, for red or black wagers, the house edge calculates to (63-60)/(63+1) = 3/64 = 4.69%. For green, it's (15-14)/(15+1) = 1/16 = 6.25%. Finally, for individual numbers, the house edge remains (63-60)/(63+1) = 3/64 = 4.69%.8Within New York State, Video Lottery Terminals (VLTs) are prominently featured at off-track betting locations. The term 'Set Point' often emerges when a Video Poker machine appears to 'heat up,' persistently yielding winning hands. This could elucidate why certain machines may be paying out on some days while remaining less accommodating on others. Additionally, many of these machines seem designed not to allow you to discard a winning hand. If you do, it will replace it or yield a superior hand. What’s your perspective on this topic?12Player 3: 139,102,293
VLTs are essentially enhanced pull-tab games, wherein a predetermined range of outcomes exists. As you play, the game randomly selects an outcome from this set and presents it to the player, whether as a slot machine or a video poker game format. Given this is a predetermined result, any notion of skill in play is superficial. For instance, if you receive a royal flush but discard it, you will likely receive another on the next draw. Typically, I note that in gambling history doesn’t hold sway, but in this context, after each play, odds can marginally improve as previous losses clear from outcomes, until the virtual supply is depleted, which presumably leads to a replenishing of the virtual pot. I contend that what you perceive as swings in luck are simply standard variations in chance, while any sense of fate is largely illusory.8What is the correct strategy for12An additional reader contributed some thoughts on this matter.
I wanted to share a thought regarding your inquiry from February 14 in the 'Ask the Wizard' section (No. 183). While it diverges from the query you addressed, it may pique your interest.
Before the approval of Proposition 1A, which enabled full class 3 gaming, we operated a small-scale installation of VLT-style machines for a pair of years. Our setup, managed by SDG (now a part of Bally), initially boasted a prize pool of 4 million draws. When that pool dwindled to 2 million, we introduced another 4 million to restore the total draws to 6 million. This cycle repeated whenever the number dropped to 2 million.
What’s the average number of rolls required to achieve a Yahtzee?12Acey Deucey12If a player consistently holds onto the most numerous card, the expected average is approximately 11.09. Below is a tablature visualizing the distribution of rolls based on a random trial of 82.6 million instances.
DelRayVA from Fairfax, VA
Backgammon ranks among my favorite gambling pastimes. My reluctance to write about it stems from the challenges in analyzing player-versus-player dynamics. I also haven’t found much opportunity for fresh insights in the game, leading me to defer to other experts. Here are some resources I recommend:
by Paul Magriel: This book is considered the cornerstone of backgammon literature. I own an old hardback copy, and it serves as an excellent starting point. Although published in 1976, its guidance remains relevant.
by Bill Robertie: I’ve been trying to navigate through this book for years and find myself stalling at about halfway. It can be discouraging when I miscalculate numerous problems, prompting me to question my backgammon skills, akin to my golf game. Nonetheless, every misstep imparts a valuable lesson, making this a crucial resource for intermediate to advanced players.
| , problem 203, or the academic paper | Game Theory and Poker | by Jason Swanson. | Dorothy from Miami, FL |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | Interest Rate with One Point |
| 12 | 507 | 0.0000000007984 | 10 years |
| 11 | 57,798 | 0.0000000910185 | 15 years |
| 10 | 2,613,754 | 0.0000041160601 | 20 years |
| 9 | 58,809,465 | 0.0000926113531 | 30 years |
| 8 | 740,999,259 | 0.0011669030492 | 40 years |
| 7 | 5,598,661,068 | 0.0088166008164 | rate function |
| 6 | 26,393,687,892 | 0.0415639752774 | In the |
| 5 | 79,181,063,676 | 0.1246919258321 | April 11, 2004 column |
| 4 | 151,519,319,380 | 0.2386080062219 | Showcase Showdown |
| 3 | 181,823,183,256 | 0.2863296074662 | Mike P. |
| 2 | 130,732,371,432 | 0.2058733541286 | Spin 1 |
| 1 | 50,840,366,668 | 0.0800618599389 | Strategy |
| 0 | 8,122,425,444 | 0.0127909480376 | Player 1 |
| Player 2 | 635,013,559,600 | 1.0000000000000 |
Another table illustrates the probabilities of improving your situation and ultimately achieving success based on how many additional dice are needed after the first roll. For instance, if a player needs three more dice to achieve a Yahtzee, the chances of reducing that to needing two after the second roll and then making the Yahtzee on the third roll is approximately 0.010288066. Player 3 .
: I engage in roughly 1000 games annually against this program. Snowie doesn’t just play exceptionally well; it also accurately highlights the cost of my mistakes in real-time. There are numerous features that I have yet to explore. One key takeaway from Snowie has been that my main hurdle lies in silly oversights—missing obvious plays, similar to chess where one poor move can undo a hundred positive moves.
: Before purchasing Snowie, I faced off against Motif countless times. In my experience, Motif presents a reliably solid strategy. Playing against a superior opponent is an effective way to refine one’s own approach.
spin
| spin | spin | spin | spin |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| spin | 175 | 125 | 300 |
spin
There's a query regarding optimal strategy in The Price is Right.
Assuming players implement the best strategy possible, what’s the likelihood of winning for each participant?
The table below illustrates each player's odds of winning according to the outcome of the first spin, where player 1 takes the first turn, followed by player 2, and player 3 going last. The final row provides the overall probabilities of victory before the initial spin.
Odds in The Price is Right Showcase Showdown. spin .