Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Participate in slot tournaments where the prizes are exceptionally large.
Ask The Wizard #413
Is there a method to carry out a Secret Santa gift exchange that follows these guidelines:
- Nobody gives a gift to themselves.
- There are no do-overs.
- No one should know more than the identity of the person they are expected to gift.
- Every match is equally likely.
Absolutely! I refer to this as the Hannah Fry technique.
- Generate a collection of cards formatted as displayed below. Each card needs to feature a distinct number at both the top and bottom. For instance, the number might be 23.
- Shuffle the cards and restack them.
- Without disturbing the order, slice each card through the middle, yielding two separate stacks.
- Cut through ONE of the stacks and ensure it is fully separated.
- Distribute the top card of each stack sequentially to all participants.
- Compile a numbered list and prompt every participant to record their assigned number.
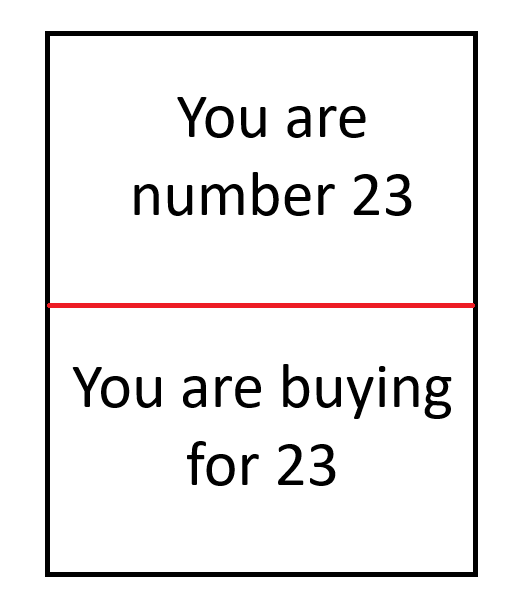
Following this process, each individual will possess two cards indicating, for instance, 'You are number 13' and 'You are responsible for number 7.' Once everyone fills out the list, they will know whom to buy for, but will remain unaware of who is purchasing a gift for them.
Source: Challenges Associated with Secret Santa - Numberphile. .
Imagine a swimming pool filled with salt water. It contains 1000 cubic meters of water. A garden hose adds fresh water to the pool at a flow rate of one cubic meter per hour. As the fresh water enters, the same amount of water exits from the pool simultaneously. How long will it take until the pool consists of only 1% salt water?
Here is my solution (PDF).
On average, how many rolls are needed for each of the Platonic solids to achieve the same side that was previously rolled?
Image source: Wikipedia
Here is the answer by number of sides.
| Sides | Avg. Rolls |
|---|---|
| 4 | 3.218750 |
| 6 | 3.774691 |
| 8 | 3.846558 |
| 12 | 5.036074 |
| 20 | 6.293585 |
Let’s analyze the case for a standard six-sided die.
- The chance that the experiment concludes within two rolls is 1/6.
- The likelihood that the experiment finishes in three rolls is (5/6)*(2/6).
- The odds of the experiment completing in four rolls are (5/6)*(4/6)*(3/6).
- The probability that the experiment wraps up in five rolls is (5/6)*(4/6)*(3/6)*(4/6).
- The chance that it concludes in six rolls is (5/6)*(4/6)*(3/6)*(2/6)*(5/6).
- The probability of the experiment concluding in seven rolls is (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6).
Define pr(n) as the probability that the experiment concludes in n rolls.
The expected rolls is: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =
2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) = 3.774691358.