Ask The Wizard #412
When playing baccarat, what are the odds that one side, either the Banker or the Player, will win at least three times compared to the other side in a shoe?
I hope you don't mind if I take a rough estimate for this calculation.
Typically, a shoe consists of around 80.88 hands. Out of these, approximately 7.70 are expected to end in a tie, resulting in 73.18 wins combined for both Banker and Player. For one side to achieve three times the victories of the other, we would need to see 54.89 wins for one and 18.30 for the other.
From the 73.18 bets that have settled, we anticipate around 37.09 wins for the Banker and about 36.09 for the Player. The standard deviation for both results is approximately 4.28. For the Banker to achieve 54.89 wins or more, it would need to be 4.16 standard deviations above the average, while the Player would need 4.39 standard deviations. The chances of either side reaching such extreme results are roughly 1 in 47,000.
This topic is actively discussed in my online forum at Wizard of Vegas .
Here are the betting odds for the winner of the 2028 presidential election. What are the chances of any other candidate winning?
| Bet | Pays |
|---|---|
| Vance | +250 |
| Newsom | +750 |
| Shapiro | +900 |
| M. Obama | +1200 |
| Buttigieg | +1400 |
| Whitmer | +1600 |
| Ramaswamy | +1600 |
| DeSantis | +2000 |
Futures betting like this usually incorporates a house edge around 30%. If we were to include a potential wager on other candidates with odds of -160, the total betting pool would contain a house edge of 29.95%. The accompanying table provides further details. The 'implied probability' indicates the likelihood if the bet was entirely fair, while the 'actual probability' reflects the fair chance for each bet relative to the total of fair probabilities. Consequently, the probability of anyone else winning stands at 43.1%.
| Bet | Pays | Implied Probability |
Actual Probability |
|---|---|---|---|
| Vance | +250 | 0.285714 | 0.200136 |
| Newsom | +750 | 0.117647 | 0.082409 |
| Shapiro | +900 | 0.100000 | 0.070048 |
| M. Obama | +1200 | 0.076923 | 0.053883 |
| Buttigieg | +1400 | 0.066667 | 0.046698 |
| Whitmer | +1600 | 0.058824 | 0.041204 |
| Ramaswamy | +1600 | 0.058824 | 0.041204 |
| DeSantis | +2000 | 0.047619 | 0.033356 |
| Field | -160 | 0.615385 | 0.431062 |
| Total | 1.427602 | 1.000000 |
The overall return is the inverse of the sum of the implied probabilities, which is 1/1.427602 = 0.700475. The sum of the return and the house edge is 1, so the house edge is 1.000000 - 0.700475 = 0.299524.
This topic is actively discussed in my online forum at Wizard of Vegas .
In the image provided below, you'll notice a yellow circle with a radius of 1. What is the area of the adjacent red circle?
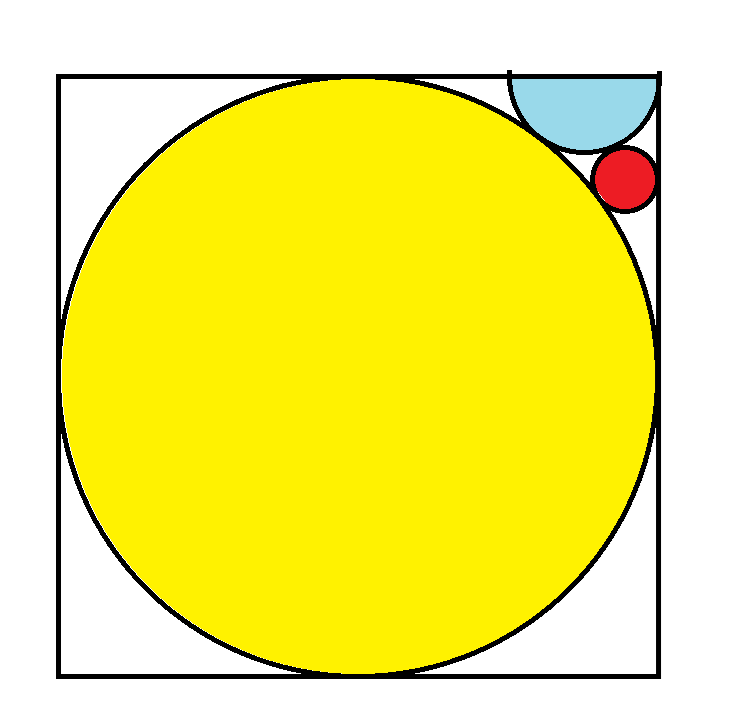
The answer is π/81 = 0.038785.
Here is my solution (PDF).
This topic is actively discussed in my online forum at Wizard of Vegas .


