Ask The Wizard #411
I argue that even if casinos operated without any house edge on their games, they would still generate profit. This can be attributed to players' poor financial management and the fact that their bankrolls are often limited compared to that of the casino. Do you see it the same way?
No, I disagree.
Effective money management in gambling is often exaggerated. Regardless of how a player approaches a game of chance like roulette, the house edge will remain intact.
Regarding the idea that casinos can simply outlast players until they run out of funds, it's also plausible that the casino might end up facing bankruptcy first. For instance, consider a player with a bankroll of $10,000 competing against an MGM-Mirage casino. At the time of writing, MGM-Mirage has a market capitalization of $11,168,000,000 . Assuming for argument’s sake that the company owns all its shares, if the player continues betting until one of them runs out of money, they would have a 1 in 1,116,801 chance of winning the entire casino. Given the high volume of players, it’s likely that eventually, one will triumph.
I understand that the number of Congressional seats for each state is determined by its population. Yet, what is the precise method used for this calculation? Is it conceivable for a state to grow in population while the national total remains constant and consequently lose a seat?
In essence, every state is guaranteed at least one Congressional seat. Subsequently, additional seats are allocated sequentially to the states that would benefit the most from them.
The process of determining which state receives the 'greatest benefit' is quite complex. Here are the specifics:
- Calculate the \"multiplier\" as the geometric mean based on (1) the percentage increase in overall seats once an extra seat is added and (2) the percentage increase in total seats if the state had one additional seat more than it currently possesses. To articulate it mathematically, if n represents the existing number of seats, the multiplier can be expressed as 1/sqrt(n*(n+1)).
- To derive the 'priority value', multiply the previously calculated multiplier by the state's population.
Perform this computation for all states. The state with the highest priority value is awarded the next available seat.
For instance, consider Nevada. The population recorded in 2020 was 3,104,614, and it has 4 seats already. The multiplier is calculated as 1/sqrt(4*5) = 1/sqrt(20) = 0.223607. Thus, the priority value amounts to 3,104,614 * 0.223607 = 694,213.
You may not have asked, but if Congress were to add another seat, the 436th, it would be allocated to New York. The table below displays the priority values for all 50 states ranked accordingly.
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| New York | 20,201,249 | 26 | 0.037743 | 762,447 |
| Ohio | 11,799,448 | 15 | 0.064550 | 761,651 |
| Texas | 29,145,505 | 38 | 0.025976 | 757,090 |
| Florida | 21,538,187 | 28 | 0.035093 | 755,842 |
| Arizona | 7,151,502 | 9 | 0.105409 | 753,835 |
| California | 39,538,223 | 52 | 0.019048 | 753,143 |
| Virginia | 8,631,393 | 11 | 0.087039 | 751,266 |
| Idaho | 1,839,106 | 2 | 0.408248 | 750,812 |
| Michigan | 10,077,331 | 13 | 0.074125 | 746,981 |
| New Jersey | 9,288,994 | 12 | 0.080064 | 743,715 |
| Pennsylvania | 13,002,700 | 17 | 0.057166 | 743,315 |
| Massachusetts | 7,029,917 | 9 | 0.105409 | 741,018 |
| Georgia | 10,711,908 | 14 | 0.069007 | 739,192 |
| Washington | 7,705,281 | 10 | 0.095346 | 734,670 |
| Illinois | 12,812,508 | 17 | 0.057166 | 732,442 |
| West Virginia | 1,793,716 | 2 | 0.408248 | 732,281 |
| Utah | 3,271,616 | 4 | 0.223607 | 731,556 |
| Tennessee | 6,910,840 | 9 | 0.105409 | 728,466 |
| Maryland | 6,177,224 | 8 | 0.117851 | 727,993 |
| Missouri | 6,154,913 | 8 | 0.117851 | 725,363 |
| Oklahoma | 3,959,353 | 5 | 0.182574 | 722,876 |
| North Carolina | 10,439,388 | 14 | 0.069007 | 720,386 |
| Louisiana | 4,657,757 | 6 | 0.154303 | 718,708 |
| Indiana | 6,785,528 | 9 | 0.105409 | 715,257 |
| Iowa | 3,190,369 | 4 | 0.223607 | 713,388 |
| Delaware | 989,948 | 1 | 0.707107 | 699,999 |
| Kentucky | 4,505,836 | 6 | 0.154303 | 695,266 |
| Wisconsin | 5,893,718 | 8 | 0.117851 | 694,581 |
| Nevada | 3,104,614 | 4 | 0.223607 | 694,213 |
| South Carolina | 5,118,425 | 7 | 0.133631 | 683,978 |
| Colorado | 5,773,714 | 8 | 0.117851 | 680,439 |
| Arkansas | 3,011,524 | 4 | 0.223607 | 673,397 |
| Minnesota | 5,706,494 | 8 | 0.117851 | 672,517 |
| Alabama | 5,024,279 | 7 | 0.133631 | 671,398 |
| Mississippi | 2,961,279 | 4 | 0.223607 | 662,162 |
| Connecticut | 3,605,944 | 5 | 0.182574 | 658,352 |
| Kansas | 2,937,880 | 4 | 0.223607 | 656,930 |
| Oregon | 4,237,256 | 6 | 0.154303 | 653,823 |
| South Dakota | 886,667 | 1 | 0.707107 | 626,968 |
| New Mexico | 2,117,522 | 3 | 0.288675 | 611,276 |
| Hawaii | 1,455,271 | 2 | 0.408248 | 594,112 |
| Nebraska | 1,961,504 | 3 | 0.288675 | 566,237 |
| New Hampshire | 1,377,529 | 2 | 0.408248 | 562,374 |
| Maine | 1,362,359 | 2 | 0.408248 | 556,181 |
| North Dakota | 779,094 | 1 | 0.707107 | 550,903 |
| Alaska | 733,391 | 1 | 0.707107 | 518,586 |
| Vermont | 643,077 | 1 | 0.707107 | 454,724 |
| Rhode Island | 1,097,379 | 2 | 0.408248 | 448,003 |
| Montana | 1,084,225 | 2 | 0.408248 | 442,633 |
| Wyoming | 576,851 | 1 | 0.707107 | 407,895 |
| Total | 330,759,736 | 435 | 0.002296 | 759,495 |
To address your second question, yes, this scenario can indeed occur. I had to spend some time examining potential cases to find one that fits. Imagine a fictional country, consisting of six states, with a total of 15 seats allocated as follows:
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| Confusion | 900 | 3 | 0.288675 | 259.807621 |
| Denial | 800 | 3 | 0.288675 | 230.940108 |
| Bliss | 700 | 3 | 0.288675 | 202.072594 |
| Depression | 600 | 2 | 0.408248 | 244.948974 |
| Limbo | 500 | 2 | 0.408248 | 204.124145 |
| Anxiety | 400 | 2 | 0.408248 | 163.299316 |
| Total | 3,900 | 15 |
Now, let’s consider a population census where numbers change substantially, yet the total population remains 3,900, with Anxiety's population increasing from 400 to 401. Despite this change, it would still be entitled to only one seat among 15 states.
| State | Population | Current Seats | Multiplier | Priority Value |
|---|---|---|---|---|
| Confusion | 1,885 | 7 | 0.133631 | 251.893721 |
| Denial | 405 | 2 | 0.408248 | 165.340558 |
| Bliss | 404 | 2 | 0.408248 | 164.932309 |
| Depression | 403 | 2 | 0.408248 | 164.524061 |
| Limbo | 402 | 1 | 0.707107 | 284.256926 |
| Anxiety | 401 | 1 | 0.707107 | 283.549819 |
| Total | 3,900 | 15 |
I want to reiterate that I had to adjust the figures considerably to discover such a situation. In general, the allocation method appears quite just.
Within a rectangle that has a height of 81, two circles are inscribed. A line segment of 56 units extends to touch both circles at the intersection point, remaining parallel to the rectangle's vertical edge.
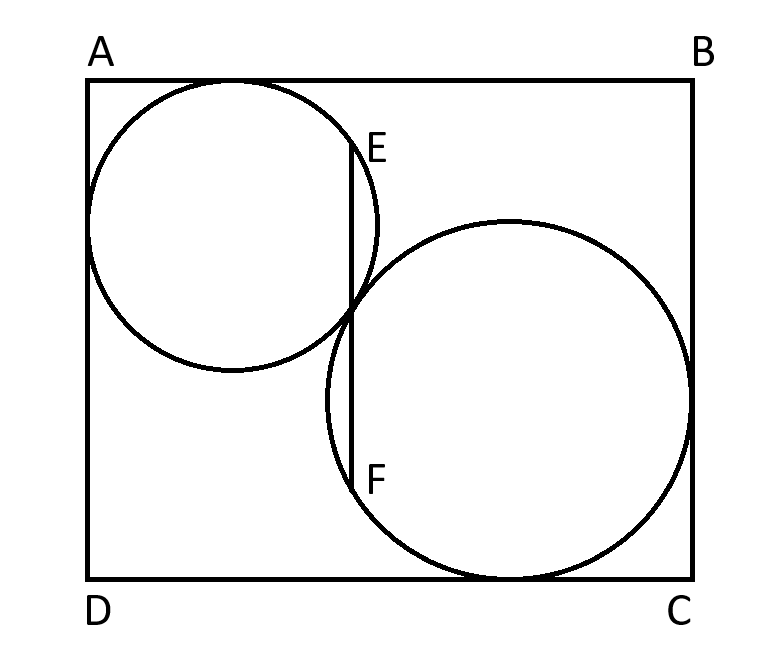
How wide is the rectangle?
Here is my solution (PDF).
This topic is being explored and discussed on my forum at Wizard of Vegas .


