Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Engage in Slot Tournaments Offering Huge Cash Prizes
Ask The Wizard #402
On your video poker calculator For the game Jacks or Better with 9-6 odds, the total number of possible hands is 1,661,102,543,100. On the other hand, your Jacks or Better page based on your information, the total number of combinations is 19,933,230,517,200. This seems inconsistent to me since I would expect both figures for combinations to match. I'm curious about the cause of this inconsistency, especially since the return rate (0.995439) remains unchanged.
Indeed, both sources refer to the same gaming variant.
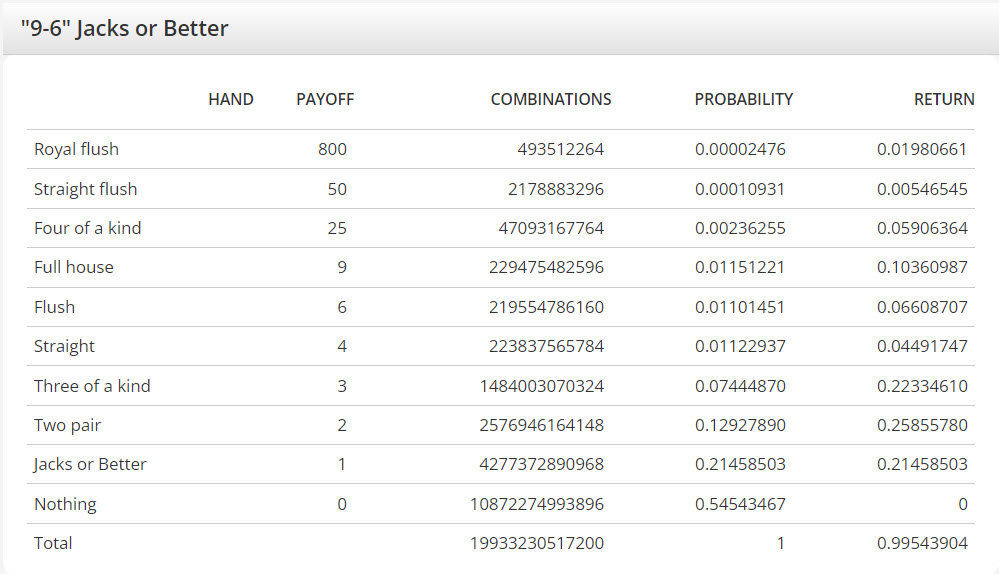
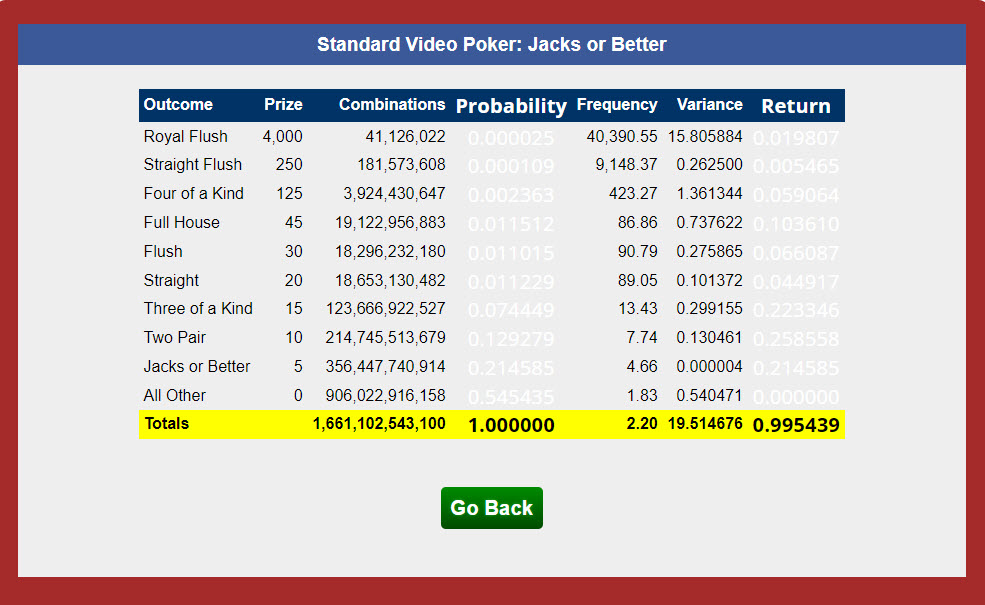
The discrepancy arises from the analytic approach applied to the game. As players discard more cards, the total combinations for the remaining draw increase. The subsequent table illustrates how many combinations are available based on the number of cards left in the deck after discarding from the original 47.
| Discards | Combinations on Draw | Weighting |
| 0 | 1 | 7,669,695 |
| 1 | 47 | 163,185 |
| 2 | 1,081 | 7,095 |
| 3 | 16,215 | 473 |
| 4 | 178,365 | 43 |
| 5 | 1,533,939 | 5 |
The least common multiple of 1, 47, 1081, 16215, 178365 and 1533939 is 7669695.
It's crucial that every initial hand maintains an equal total weight. To ensure this balance, I implement a weighting system for each hand that corresponds to the quantity of discarded cards. You'll find this weighting factor listed in the right column of the preceding table. The multiplication of the number of draw combinations with the weighting factor will invariably yield 7,669,695.
Calculating the combinations of five cards from a deck of 52 yields combin(52,5) = 52!/(47!*5!) = (48*49*50*51*52)/(1*2*3*4*5) = 2,598,960. Thus, the overall number of combinations in video poker according to my calculations is formulat(52,5) * formulat(47,5) * 5 = 2,598,960 * 7,669,695 = 19,933,230,517,200. That explains why this figure appears frequently in my combination tables.
You might wonder why the calculator returns 1,661,102,543,100. This particular calculator was developed by the talented video poker programmer JB, who incorporated an additional step to compute the greatest common multiple of the combinations per hand. This least common multiple typically equals 12. Regardless of its value, he divided each combination count by this multiple. I believe he prefers to keep the numbers manageable while ensuring they remain precise.
Consider a one-meter rubber band with an ant positioned at one end. Each day, this ant moves one centimeter forward, but at day’s end, the rubber band stretches by an additional meter. How much time will it take for the ant to traverse to the opposite side?
Be advised that this is a challenging question. In the spoiler section below, I've provided some tips that may assist you in figuring it out.
Euler's Constant (this should not be confused with Euler's number)
Here is my solution (PDF).
This question has been brought up and thoroughly debated in my forum at Wizard of Vegas .
Recently, my friend and I managed to land two out of three Megabucks symbols. What are the odds of that happening?
According to my own page on Megabucks Each reel's total weight amounts to 368, with the Megabucks symbols assigned a weight of 1. Therefore, the chance for any specific reel to stop on a Megabucks symbol is 1 in 368.
The probability of getting exactly 2 out of 3 is 3 × (1/368) * (1/368) × (367/368) = 0.0000220924 = in 1/45,264.