Ask The Wizard #399
Have you ever noticed that when you remove a small square from the initial image and rearrange the pieces, the overall area appears unchanged? How can this occur?
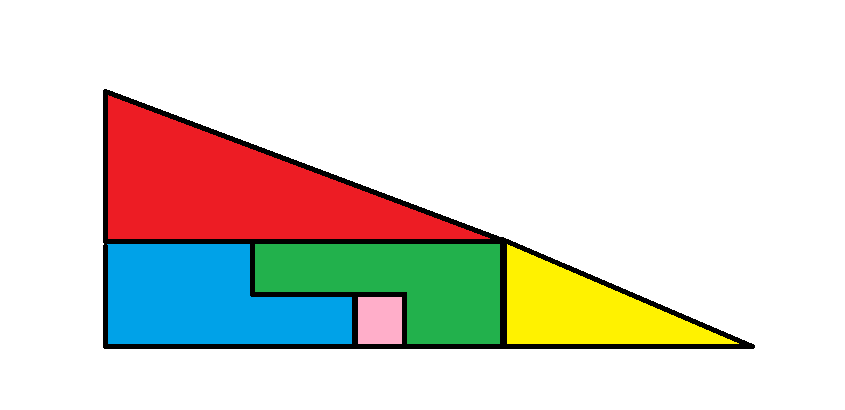
Image 1
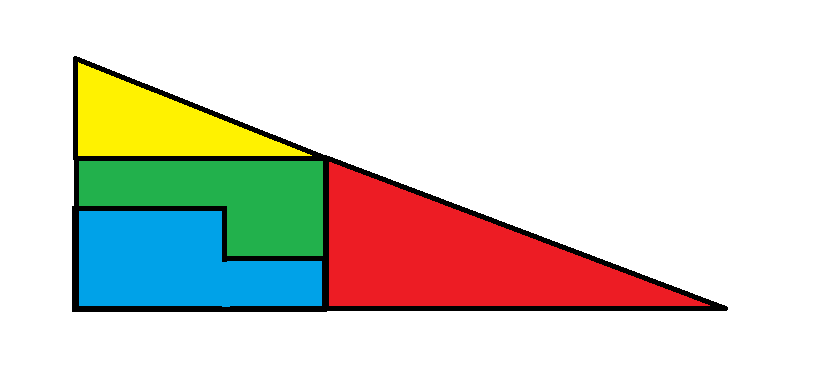
Image 2
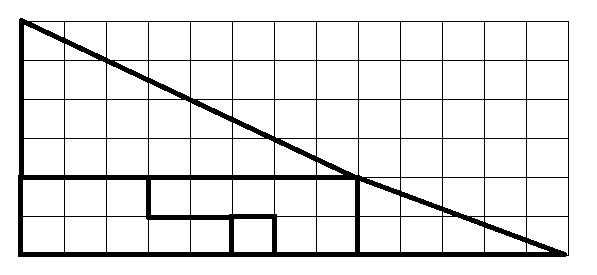
The illustration above presents the original image arranged on a grid, allowing for a clearer view of each segment's dimensions.
Observe that the large red triangle has sides measuring 4 and 8 units. In contrast, the smaller yellow triangle measures 2 and 5 units. This indicates that the two triangles are not in proportion. The hypotenuses of both triangles are not aligned the same way in the two figures; one has a slope of 0.5, while the other has a slope of 0.4. When positioned as they are in either figure, it creates an illusion of forming a larger triangle with sides measuring 5 and 13 units, but it doesn’t actually form a triangle.
The area of the red triangle is 4*8/2 = 16.
The area of the yellow triangle is 2*5/2 = 5.
In the first depiction, the remaining three pieces assemble a rectangle with dimensions of 2 by 8, resulting in a total area of 16.
In the subsequent image, the other two segments align to form a rectangle measuring 3 by 5, yielding an area of 15.
Calculating the total area of the first illustration, we have the red triangle plus the yellow triangle plus the large rectangle, which totals 16 + 5 + 16 = 37.
In the second illustration, the total area consists of the red triangle plus the yellow triangle plus the smaller rectangle, summing up to 16 + 5 + 15 = 36.
To summarize, the first image is larger when it includes the small square. It's an optical illusion that the combined pieces appear to constitute a large triangle in both cases, but they don’t.
Imagine 16 motorcycles stationed at the verge of an expansive desert. Each bike can cover a distance of 100 miles on a full tank of fuel, and all motorcycles begin their journey with full tanks. Transferring fuel between motorcycles is permissible. The objective is to determine how far one motorcycle can travel from the starting point.
The essential aspect of tackling this issue involves the group making an initial short journey. After this, they can consolidate the remaining fuel from one motorcycle to refill the tanks of the others.
For instance, at the outset, divide a full tank of gas into 16 equal portions, allocating one to each motorcycle. Then, all the motorcycles travel together until 1/16 of a tank is used, which propels them 100/16 = 6.25 miles. Afterward, siphon 15/16 of a tank from one motorcycle to top off the other 15 motorcycles by adding 1/16 of a tank to each.
Next, continue this process with 15 motorcycles, traveling as far as 1/15 of a tank allows, equivalent to 100/15 = 6.666667 miles. Then, extract 14/15 of a tank from one motorcycle and distribute 1/15 of a tank to the remaining 14 motorcycles.
Continuing in this process will get the last motorcycle a total distance of (1/16) + (1/15) + (1/14) + ... + (1/1) = 338.072899 miles.
This query was raised and deliberated in my forum at Wizard of Vegas .
What opinions do you have regarding the Sleeping Beauty Paradox?
For the sake of clarity for other readers, let's outline what the Sleeping Beauty Problem or Paradox involves.
Sleeping Beauty (SB) consents to participate in an experiment. All elements of the experiment are explained to her in detail and accurately:
- On Sunday: SB is put to sleep. Once she's asleep, a fair coin will be flipped.
- On Monday: She will awaken and be asked, 'What is the probability that the coin landed on heads?' After providing her answer, she will be returned to sleep with an amnesia-inducing drug, which will erase all memories of Monday.
- On Tuesday: If the coin shows tails, the sequence that occurred on Monday will repeat. If it shows heads, she will simply continue to sleep throughout that day.
- On Wednesday: SB will be awakened again, not asked any questions, and will return home as the experiment concludes.
The crux of the question is how she ought to respond to the query posed on Monday, and possibly again on Tuesday.
My Answer
If this experiment were conducted a million times, we would anticipate encountering three types of awakenings, each occurring with equal frequency:
- The coin lands on heads, resulting in an awakening on Monday.
- The coin lands on tails with an awakening on Monday.
- The coin lands on tails with an awakening on Tuesday.
This is because the awakenings that take place on Monday should be evenly distributed between the outcomes of heads and tails. Furthermore, if the coin lands on tails, the Monday and Tuesday awakenings will be equally divided. As a result, all three categories will see a similar number of awakenings over a large sample.
Out of these awakenings, one-third will occur subsequent to a heads being flipped. Thus, the probability that the coin landed on heads is calculated to be 1/3.
Conversely, the 1/2 group posits that SB receives no new information upon each awakening, and therefore should presume that each result of the coin flip was equally probable.
In response, I would extend this to consider 999,999 awakenings following a tails result. Only one in a million awakenings would happen following a heads flip. Therefore, it's quite reasonable to think that upon any awakening, it was likely one of the 999,999 occurrences following a tails. Essentially, in this case, the accurate answer would be 1 in 1,000,000.
To expand further, imagine if SB was asked to predict the result of the coin flip with each awakening. Successfully predicting it would earn her $1,000. If she consistently chose 'heads', she could anticipate an expected gain of (1/2) * $1,000 = $500. Conversely, if she consistently opted for 'tails', her expected gain would be (1/2) * $2,000 = $1,000. Thus, the very act of waking SB suggests a higher likelihood of the coin landing on tails.
If my explanation was not clear the Sleeping Beauty Problem Wikipedia delves into this paradox more comprehensively than I do, presenting various potential responses from SB.
This query was raised and deliberated in my forum at Wizard of Vegas .


