Ask The Wizard #395
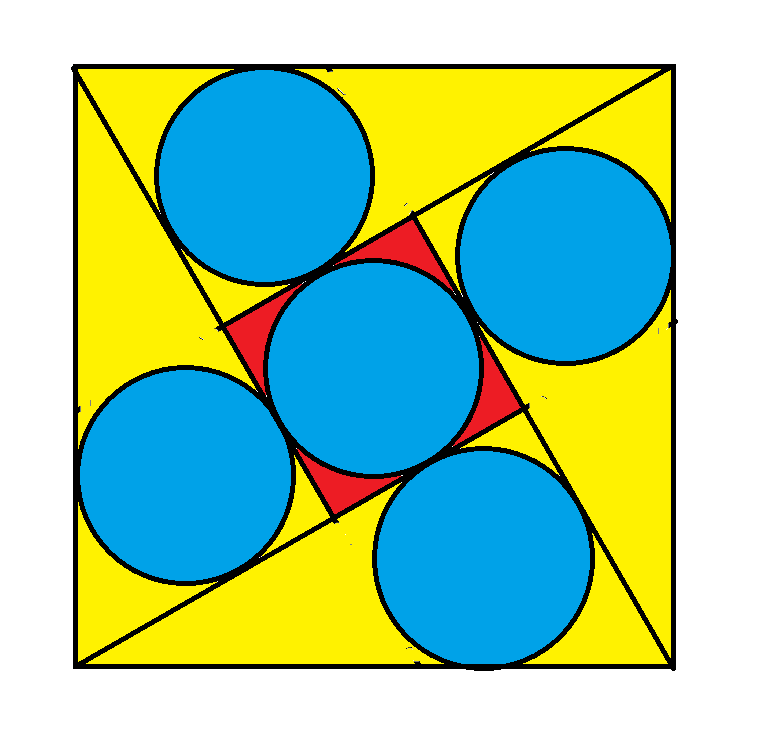
The illustration depicted features four right triangles with a smaller square nestled within a larger square. The side length of the larger square is one unit. All five circles share the same diameter. What is the measurement of the radius?
radius = (sqrt(3)-1)/4 = 0.183013.
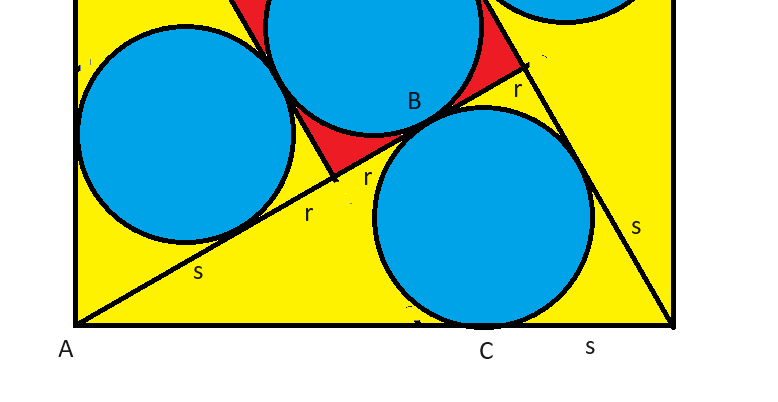 Let's take a closer look at one of the triangles and outline our approach:
Let's take a closer look at one of the triangles and outline our approach:
- r = Radius of the circles
- s = The distance from any vertex of the larger square to the point where the nearest circle touches the triangle in which it is inscribed.
If we examine the triangle shown in the image, the distances are as follows:
- short leg = r+s
- long leg = 3r+s
- hypotenuse = 1
Using the Pythagorean formula:
(r+s)2+ (3r+s)2= 1
r2+ 2rs + s2+ 9r2+ 6rs + s2= 1
10r2+ 2s2+ 8rs = 1
We will need another equation to arrive at a solution. Considering the side length of the large square, which is given as one unit, we find that AB = AC. Here, AB can be expressed as 2r + s, making AC also equal to 2r + s. The remainder of the large square's side is represented by s. Thus:
2r + 2s = 1.
2s = 1-2r
s = 1/2 - r
Now, let's substitute this into our equation derived from the Pythagorean theorem:
10r2+ 2(1/2 - r)2+ 8r(1/2 - r) = 1
10r2+ 2(1/4 - r + r2) + 4r - 8r2= 1
2r2+ 1/2 - 2r + 2r2+ 4r = 1
4r2+ 2r - 1/2 = 0
8r2+ 4r - 1 = 0
Using the quadratic equation:
r = (-4 +/- sqrt(48))/16
r = (sqrt(3)-1)/4 = 0.183013.
This problem was taken from the Mind Your Decisions On the YouTube channel, Presh provides a solution that does not involve the Pythagorean theorem.
This challenge has been presented and discussed in my online forum at Wizard of Vegas .
What are your thoughts on the 'Right and Wrong Way System'? Here's how it works: a player starts with a don’t pass bet of one unit. If a point is established, the player places a one-unit wager on that number. If that number comes up, the player earns a profit; however, if a seven is rolled, they break even. It appears to present a free betting scenario. What am I overlooking?
Let’s presuppose that when the point is either 4 or 10, the player pays a 5% commission solely on winnings. We will adhere to the Vegas rule where rolling a 12 on the come-out roll results in a push for the don’t pass bet (for example, in Northern Nevada, a roll of 2 results in a push). Based on this, here are all the possible outcomes:
- If the come-out roll is a 2 or 3: The player wins one unit on the don’t pass bet.
- If the come-out roll is a 12: The player pushes on the don’t pass bet.
- If the come-out roll is a 7 or 11: The player loses on the don’t pass bet.
- If the point is either 4 or 10 and wins: The player earns 1.95 units from the buy bet but loses one unit from the don’t pass, leading to a net gain of 0.95 units.
- If the point is either 5 or 9 and wins: The player gains 1.4 units from the place bet, loses one unit from the don’t pass, resulting in a net win of 0.4 units.
- If the point is either 6 or 8 and wins: The player receives 7/6 units from the place bet while losing one unit on the don’t pass, culminating in a net gain of 1/6 units.
- If the point is either 4 or 10 and loses: The player loses one unit from the buy bet while winning one unit from the don’t pass, resulting in a net push.
- If the point is either 5 or 9 and loses: The player loses one unit on the place bet but wins one unit from the don’t pass, resulting in a net push.
- If the point is either 6 or 8 and loses: The player loses one unit on the place bet while winning one unit from the don’t pass, leading to a net push.
The subsequent table outlines all potential outcomes. It details the probabilities, winnings, and contributions to the return from every outcome. The bottom right corner indicates an anticipated loss of 0.02951 units.
Right and Wrong Way System
| Event | Pays | Probability | Return |
|---|---|---|---|
| Come out 2 or 3 | 1 | 0.083333 | 0.083333 |
| Come out 12 | 0 | 0.027778 | 0.000000 |
| Come out 7 or 11 | -1 | 0.222222 | -0.222222 |
| Point 4 win | 0.95 | 0.027778 | 0.026389 |
| Point 5 win | 0.4 | 0.044444 | 0.017778 |
| Point 6 win | 0.166667 | 0.063131 | 0.010522 |
| Point 8 win | 0.166667 | 0.063131 | 0.010522 |
| Point 9 win | 0.4 | 0.044444 | 0.017778 |
| Point 10 win | 0.95 | 0.027778 | 0.026389 |
| Point 4 loss | 0 | 0.055556 | 0.000000 |
| Point 5 loss | 0 | 0.066667 | 0.000000 |
| Point 6 loss | 0 | 0.075758 | 0.000000 |
| Point 8 loss | 0 | 0.075758 | 0.000000 |
| Point 9 loss | 0 | 0.066667 | 0.000000 |
| Point 10 loss | 0 | 0.055556 | 0.000000 |
| Total | 1.000000 | -0.029512 |
The reason this strategy has a negative expected value lies in the come-out roll. There are three ways to win with a 2 or 3 but eight ways to lose with a 7 or 11. While it’s true that if a player navigates past the come-out roll, they gain positive equity, it’s insufficient to offset the expected loss incurred during the come-out roll.
My wife tends to be angry 20% of the time. When posed with the question 'Are you angry?', she responds 'no' 90% of the time when she is indeed angry. Conversely, if she is not angry, she answers 'no' 95% of the time. I'm curious about the probability that she is angry based on her response.
This scenario exemplifies a classic problem in Bayesian probability.
If her response is 'no', the probability that she is upset is 9/47, which equates to 19.15%.
If her response is 'yes', the probability that she is angry becomes 1/3, or 33.33%.
The formula for determining probabilities in conditional statements can be articulated as probability(both A and B)/probability(B).
In the instance of a 'no' response, the probability she is angry is calculated as (0.2*0.9)/(0.2*0.9 + 0.8*0.95) = 0.18/0.94 = 9/47.
In the case of a 'yes' reply, the probability she is upset is computed as (0.2*0.1)/(0.2*0.1 + 0.8*0.05) = 0.02/0.06 = 1/3.


