Ask The Wizard #383
Alice and Bill together can finish painting a house in 3 hours.
When Alice teams up with Cindy, they are able to paint a house in 4 hours.
Bill and Cindy, when collaborating, take 5 hours to complete the painting of a house.
How long does it take if they all paint?
Here is my solution (PDF).
Imagine a rubber band stretched across two neighboring circles with diameters of 2 and 5. What would be the total length of the extended rubber band?
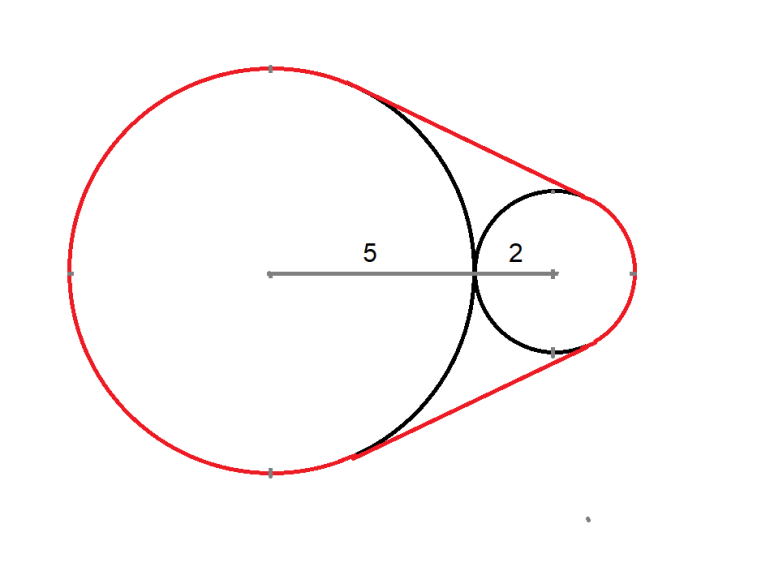
Here is my solution (PDF).
This question is being raised and examined in the discussions on my forum found at Wizard of Vegas .
Picture a game of rock-paper-scissors where the following rules apply:
- In the event rock defeats scissors, the winner receives $1 from the loser's bet.
- If scissors triumph over paper, the winnings for scissors amount to $2 from paper's stake.
- If paper beats rock, rock pays paper $3
- No money changes hands on a tie
If two logical thinkers are competing, what should be the best approach for each player?
- Play paper with probability 1/6
- Play rock with probability 1/3
- Play scissors with probability 1/2
Let’s outline some probabilities for the logician aiming to maximize his profits:
- r = Probability of playing rock
- p = Probability of playing paper
- s = Probability of playing scissors
It's clear that r+p+s = 1. Given r and p, s = 1-r-p.
In a scenario where both logicians are playing, they would be indifferent to the choices of their opponent, particularly if they randomize their selections.
The predicted gain from the opponent playing rock is calculated as: 3p - (1 - r - p) = 4p + r - 1.
For the opponent playing paper, the expected earnings would be: 2(1 - r - p) - 3r = 2 - 5r - 2p.
When the opponent chooses scissors, the anticipated win is: r - 2p.
These three equations must all yield the same result.
By equating the first and third equations, we find:
4p+r-1 = r - 2p
p = 1/6
By equating the first and second equations, we arrive at:
2 -5r - 2p = 4p + r -1
We already have that p=1/6, which conveniently allows us to deduce that r=1/3.
s=1-r-p = 1-(1/3)-(1/6) = 1/2.
Therefore, each player should choose paper with a probability of 1/6, rock with a probability of 1/3, and scissors with a probability of 1/2.
In a broader context, the strategy for this puzzle is to allocate each selection based on the potential monetary changes that would happen if the other two symbols were chosen.
This question is being raised and examined in the discussions on my forum found at Wizard of Vegas .


