Ask The Wizard #373
If you're a fan of The Big Bang Theory, you'll likely remember the iconic Rock Paper Scissors Lizard Spock game. It's a fun twist on the traditional game featuring five different symbols, each with its own rules:
- Paper covers rock
- Rock crushes lizard
- Lizard poisons Spock
- Spock smashes scissors
- Scissors cuts paper
- Lizard eats paper Spock vaporizes rock
- Scissors decapitates lizard
- Paper disproves Spock
- Rock crushes scissors
I wonder if it’s possible to introduce additional symbols in this game while maintaining equal chances for each symbol against a randomly selected opponent?
Yes, I love that scene too! Here is a YouTube video of it.
To keep it fair, you should work with an odd number of symbols. Although you could theoretically use an even number, you’d need to create ties for certain symbol pairs, which defeats the purpose. Ideally, we should have clear outcomes where ties only occur when both players choose the same symbol.
A particularly straightforward solution can be illustrated using a prime number of symbols. Let’s take seven symbols as an example, ranging from A to G, and imagine them arranged in a circle, as depicted in this diagram.
Start with symbol A, directing an arrow to the next symbol in a clockwise motion. This arrow will indicate which symbol defeats the other. Picture it as if that symbol were hit by an arrow. Continue this process in a clockwise direction until you return to A. The resulting diagram will appear as follows:
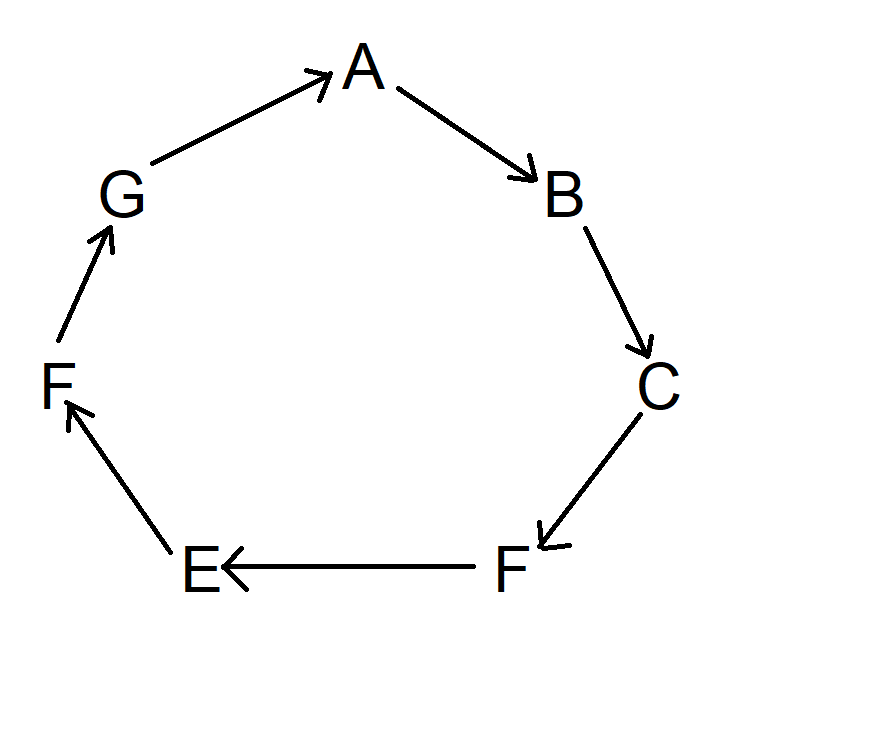
Now, replicate this process, but this time move two symbols clockwise starting from A. Actually, you are free to start from any symbol you prefer. The updated diagram should look like this:
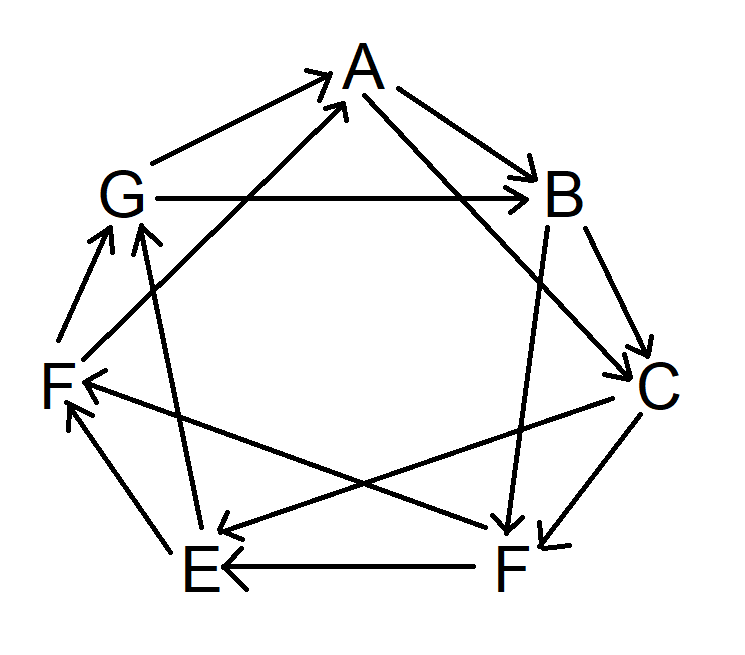
In the final step, repeat the same procedure but advance three symbols clockwise. The resulting diagram will come out as follows:
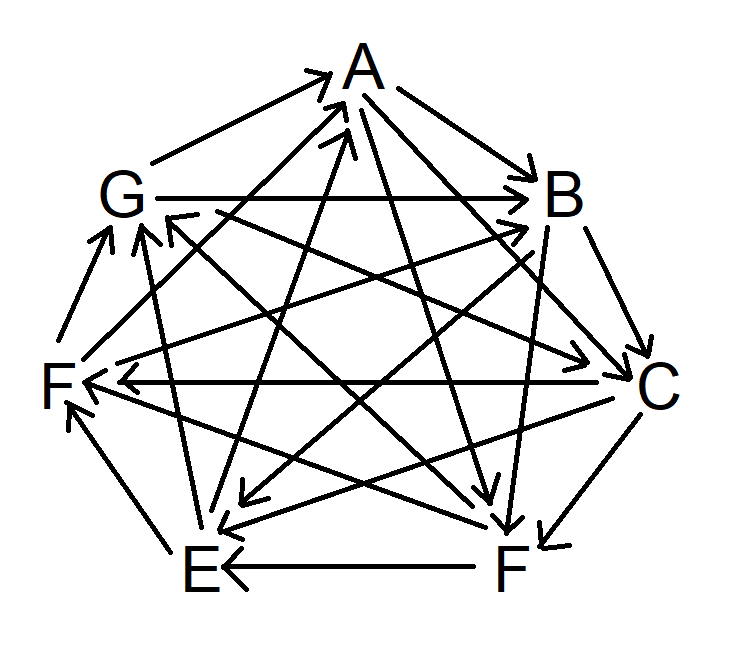
At this stage, you can observe that each symbol defeats three others and is defeated by three unique symbols in return.
This technique will prove effective for any prime number of symbols. By the time you loop back to the starting symbol, you will have encountered all the symbols in the circle. For 'n' symbols, you need to perform this exercise (n-1)/2 times.
You can create a balanced game using any odd number of symbols. However, be cautious as you may occasionally return too quickly to the original symbol. In such cases, you will need to establish additional loops starting from the unvisited symbols.
This particular topic is one of the discussions in my forum at Wizard of Vegas .
What is the likelihood of achieving a tie in Three Card Poker?
The exact answer is 450528/407170400 = 0.001106485 = 1/904.
The table below outlines the various combinations for forming each type of initial hand along with the number of ways that can result in a tie for the second hand. It's important to consider whether the initial hand includes two or three suits when dealing with straights versus weaker hands.
In the bottom right corner, you can see that there are 450,528 ways to achieve a tie in Three Card Poker. The total number of pairwise combinations for two hands is calculated as combin(52,3)*combin(49,3), which equals 407,170,400. Therefore, the probability is 450,528 divided by 407,170,400.
Three Card Poker Tie
| Hand | Hand 1 | Hand 2 | Product |
|---|---|---|---|
| Three of a kind | 52 | 0 | 0 |
| Straight flush | 48 | 3 | 144 |
| Straight (three suits) | 288 | 26 | 7,488 |
| Straight (two suits) | 432 | 25 | 10,800 |
| Flush | 1,096 | 3 | 3,288 |
| Pair | 3,744 | 3 | 11,232 |
| Junk (three suits) | 6,576 | 26 | 170,976 |
| Junk (two suits) | 9,864 | 25 | 246,600 |
| Total | 22,100 | 450,528 |
How much is a complimentary ace coupon worth in a 6-5 blackjack game?
In my value of a free ace On one page, I indicate that its value is equivalent to 50.1844% of the bet amount used in a 3-2 blackjack game.
In a six-deck version of blackjack, if you start with an ace as your first card, the probability of drawing a winning blackjack is 29.3139%. In this scenario, you win 0.3 less units in a 6-5 blackjack game compared to a 3-2 game.
Thus, the worth of a free ace in a 6-5 six-deck blackjack scenario is calculated as 50.1844% × 29.3139 × 0.3, which amounts to 41.3902% of your initial bet.
Someone placed a bet with me claiming they could roll a total of 12 with two dice within 27 attempts. If they fail, I would win even money. Given that the probability of rolling a 12 is 1/36, shouldn't it take an average of 36 rolls to achieve that? It seems that the odds are in my favor since my opponent only has 27 attempts. Am I right, or is there an error in my reasoning?
While the average time between rolling a 12 is indeed 36 rolls, which includes the roll that results in 12, this doesn't mean they appear precisely every 36 rolls. The chance of NOT rolling a 12 is (35/36). Multiplying this probability across 27 rolls yields (35/36)^27. Therefore, the likelihood of rolling at least one 12 is calculated as 1 - (35/36)^27, which is about 53.26%.
The subsequent table illustrates the chances of rolling at least one 12 across a range of 20 to 36 rolls. It's noteworthy that you need to reach 25 rolls to gain an edge at even odds.
Probability 12
| Rolls | Probability |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |


