Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Exciting slot competitions offering enormous prize pools
Ask The Wizard #371
I noticed that Alaska has implemented ranked choice voting for Congressional elections. In the case of the 2022 election, where there were 22 candidates vying for a single House seat and approximately 200,000 total votes cast, what would be the minimum number of first-choice votes required for the eventual winner?
For those who may not be acquainted with the mechanics of ranked choice voting:
- Electorate participants are requested to order their preferred candidates from first to last.
- If any candidate secures the majority of the votes, that individual is declared the winner.
- If no candidate achieves a majority, the candidate with the fewest votes is removed from the race. During this process, all other candidates ranked lower than the eliminated candidate ascend one position in ranking.
- Votes are recounted.
- Repeat the second step until a candidate attains a majority of votes.
*: Apologies for using the term 'he.' My intention is to refer to 'he or she'; however, I find it cumbersome to repeat this every time I mention a pronoun. Additionally, I consider the use of 'they' to be grammatically incorrect, as it is intended to denote multiple individuals.
As an illustration, imagine a scenario with 11 voters and four contenders. The rankings for the candidates by those eleven voters are as follows:
| Choice 1 | Choice 2 | Choice 3 | Choice 4 |
| B | A | C | D |
| C | B | A | D |
| C | A | D | B |
| D | A | C | B |
| A | D | B | C |
| B | A | D | C |
| B | D | A | C |
| B | D | C | A |
| C | D | B | A |
| A | D | B | C |
| A | B | D | C |
Here’s how the first-round vote distribution looks:
| Candidate | Rank 1 Votes |
| A | 3 |
| B | 4 |
| C | 3 |
| D | 1 |
Since no candidate received the majority of first-choice votes, the last-place candidate D is eliminated. He essentially disappears from the vote count, and every candidate ranked behind him moves up one spot, resulting in the following arrangement:
| Choice 1 | Choice 2 | Choice 3 |
| B | A | C |
| C | B | A |
| C | A | B |
| A | C | B |
| A | B | C |
| B | A | C |
| B | A | C |
| B | C | A |
| C | B | A |
| A | B | C |
| A | B | C |
Below is the tally of first-place votes during the second round of voting:
| Candidate | Rank 1 Votes |
| A | 4 |
| B | 4 |
| C | 3 |
In the second round, no candidate achieved a majority in the first-place votes, leading to the elimination of candidate C. Following C's exit, the distribution of votes in the third round becomes:
| Choice 1 | Choice 2 |
| B | A |
| B | A |
| A | B |
| A | B |
| A | B |
| B | A |
| B | A |
| B | A |
| B | A |
| A | B |
| A | B |
Below is the tally of first-place votes during the second round of voting:
| Candidate | Rank 1 Votes |
| A | 5 |
| B | 6 |
Candidate B emerges victorious in the election, garnering six votes by the third round.
To address your inquiry regarding a scenario with 22 candidates and 200,000 votes: it is conceivable for a candidate to win with as few as two first-place votes. There are multiple potential scenarios wherein this could occur. For instance, consider this breakdown of first-place vote totals:
| Candidate | Total First Place |
| A | 85,311 |
| B | 57,344 |
| C | 28,672 |
| D | 14,336 |
| E | 7,168 |
| F | 3,584 |
| G | 1,792 |
| H | 896 |
| I | 448 |
| J | 224 |
| K | 112 |
| L | 56 |
| M | 28 |
| N | 14 |
| O | 7 |
| P | 2 |
| Q | 1 |
| R | 1 |
| S | 1 |
| T | 1 |
| U | 1 |
| V | 1 |
| Total | 200,000 |
If all voters, except for those who selected candidate P as their first choice, rank P as their second choice, then P is poised to win.
In reality, P doesn't necessarily need to be consistently in second position. P could be the second choice for only the six voters who placed candidates Q, R, S, T, U, and V in first place. In subsequent rounds, it would not negatively impact P even if previously eliminated candidates were ranked higher than P.
Imagine a semicircle with a radius of 1 that contains two rectangles arranged one atop the other. What is the maximum total area that can be achieved by these two rectangles?
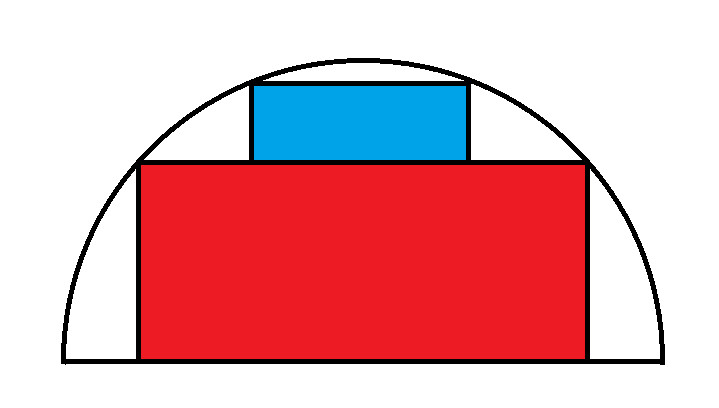
Here is my full solution (PDF).
This intriguing question is being explored in my discussion forum at Wizard of Vegas .
Do unicorns have wings?
No.
A mythical winged horse with a horn is known by various names, including cerapter, pegacorn, alicorn, or unisus. Just to clarify, a winged horse without a horn (of which I know only one specific example) is called Pegasus. Meanwhile, a unicorn possesses a horn, but lacks wings.
For the sake of this discussion, please disregard identical twins and assume each child has an equal chance of being male or female. If children are randomly sampled from families consisting of 2 to 5 members, what is the likelihood that a boy or girl will have a sister?
Interestingly, the probability remains consistent for both genders, irrespective of the size of the family.
Let's examine families with three children, for example. Here are the eight potential arrangements of boys and girls, considering their order:
BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG
If you randomly select any girl from the list, you'll find that out of the 12 girls, 9 have at least one sister. The same is true for the 12 boys; 9 have sisters as well. Thus, the probability can be calculated as 9 out of 12, which simplifies to 3/4.
To determine the probability for any child to have a sister within a family of n children, the general formula is 1 - (1/2)n-1.
Here are the probabilities of having a sister based on the total number of siblings in the family:
- 1: 0
- 2: 1/2
- 3: 3/4
- 4: 7/8
- 5: 15/16
- 6: 31/32
Moreover, it seems logical that the probabilities would be identical for boys and girls, as the gender of your siblings does not depend on your own gender. Therefore, what matters is the size of the family rather than individual gender.
This intriguing question is being explored in my discussion forum at Wizard of Vegas .