Ask The Wizard #367
In craps, I prefer to place bets on all possible numbers. What is the expected count of unique numbers I might roll before hitting a total of seven?
For clarity, the question pertains to determining how many of these totals will appear when rolling two dice before rolling a seven: 4, 5, 6, 8, 9, and 10.
The expected outcome is approximately 2.38. The table below illustrates the likelihood of rolling anywhere from zero to six unique totals from the specified range, with the bottom right cell reflecting the mean number of unique totals rolled prior to rolling a seven.
Unique Numbers Rolled
| Total | Probability | Expected |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| Total | 1.000000 | 2.375758 |
Is it accurate to say that when flipping a fair coin, it has a higher chance of landing on the side that was initially facing up?
The evidence suggests this is true!
Researchers Persi Diaconis and Susan Holmes from Stanford University analyzed a total of 10,000 coin flips. They found that the coin showed the same side face up that it started with in 50.8% of the instances (source: from the newsletter What's Happening in the Mathematical Sciences by the American Mathematical Society). The probability of achieving a ratio this high or greater is calculated to be 5.48%. The Fifty-one Percent Solution To substantiate this mathematically, I assumed the actual revolutions of a coin followed a Poisson distribution. Specifically, for a mean number of revolutions represented by m, the probability of exactly n revolutions is given by exp(-m)*m^n/n!. The graph below illustrates the Poisson distribution for the possibilities of 0 to 25 revolutions, taking a mean of 10 into account.
The reason behind my choice of the Poisson distribution is that it closely resembles a bell curve for sufficiently high means, and it cannot yield negative values.
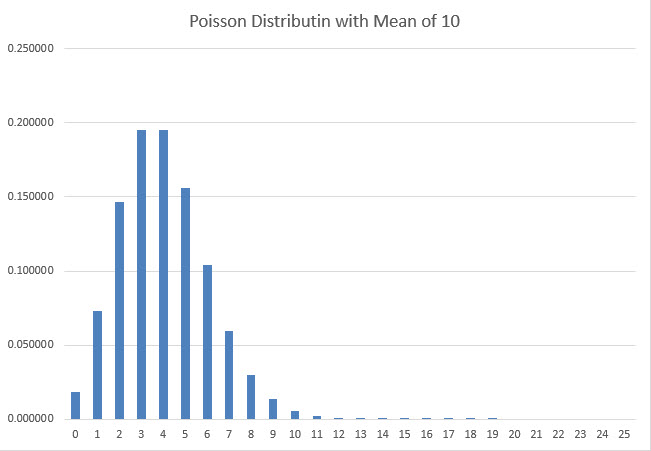
Next, I determined the probability of obtaining an even number of half-revolutions (which results in the same side facing up as the starting position) based on different mean values for half revolutions. The table below summarizes my findings for means ranging from 0.5 to 5.0.
Probability of Having Even vs Odd Number of Revolutions
I began to ponder why the likelihood of an even number was always above 50%. It turns out that the probability of an even number, given a mean m, can be mathematically expressed as 0.5 + e^(-2m)/2. Since e raised to any power is always a positive value, the likelihood of having an even number of revolutions is consistently positive.
| Mean Revolutions | Even Total | Odd Total |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
What are your thoughts on the Spelling Bee segment from The Price is Right?
You can see my proof of this formula here .
To aid other readers, let me briefly outline the game's rules.
The game features a board consisting of 30 cards, each numbered from 1 to 30.
- Each card has a letter or the word 'car' printed on its reverse side, with the following distribution:
- The host allows the contestant to select two cards.
- C: 11
- A: 11
- R: 6
- Car: 2
- Following a pricing game, which I won't detail here, the contestant has the chance to earn up to three additional cards.
- There are two possible ways the contestant can win a car:
- The cards will be flipped over.
- The contestant must collect at least one card for each letter, thus forming the word CAR.
- The contestant needs at least one of the 'CAR' cards.
- At any moment during the game, the contestant can opt to drop out and receive $1,000 for each card they haven’t revealed.
- The table below outlines the winning probabilities based on the total number of cards the player possesses, assuming none have been flipped over yet.
Here is a clip of the game being played.
Spelling Bee — Winning Probability
When no cards have been flipped, the contestant should refrain from surrendering, provided the car's value is reasonably substantial. For instance, even with just two cards, the contestant has approximately a 13.1% chance of having at least one 'CAR' card. The contestant would be indifferent to a surrender value of $2,000 if the car was valued at $15,263.16, as any new car would likely exceed this amount.
| Cards | Probability Winning |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
Here are the points of indifference regarding the car's value, based on the number of cards the contestant has yet to reveal.
Correct strategies and insights for casino games such as blackjack, craps, roulette, and countless others that can be enjoyed.
When no cards have been flipped, the contestant should refrain from surrendering, provided the car's value is reasonably substantial. For instance, even with just two cards, the contestant has approximately a 13.1% chance of having at least one 'CAR' card. The contestant would be indifferent to a surrender value of $2,000 if the car was valued at $15,263.16, as any new car would likely exceed this amount.
| Cards | Indifference Point |
|---|---|
| 2 | $15,263.16 |
| 3 | $8,066.23 |
| 4 | $6,849.11 |
| 5 | $6,803.75 |


