Ask The Wizard #365
I've heard that the threshold for taxable winnings from slot machines has risen from $1,200 to $5,000. Is that accurate?
No.
A proposed law seeks to make that change. However, many proposed laws don't progress, so players shouldn't get overly excited.
If I had the opportunity to vote, I would enthusiastically support the increase. The $1,200 limit hasn't changed since 1977. Based on the research from the American Institute for Economic Research , the value of $1,200 in 1977 would equate to around $5,336 in 2021. I could easily argue against taxing gambling winnings altogether. Yet, realistically, that idea is unlikely to gain traction, so at the very least, we should adjust the taxable jackpot threshold for inflation, which should have been done from the start.
For more information, please read The proposed legislation aims to raise the threshold for reporting slot machine jackpot taxes to $5,000. at the Las Vegas Sun.
Imagine a square with a side length of 1. Each corner of this square has a circle with a radius of one. What is the area of the red region where the circles overlap?

0.3151467436277204526267681195872952611229178793146546456025078846506724518532
696291281987550234571136517565540890207325190613364415179082650967976239484533
906220014689983405916338783947732316433868623061639270583186549287254862947423
40423083863353504721515...
Here is my solution (PDF).
This topic is being discussed in my forum at Wizard of Vegas .
Picture a circular grassy field with a radius of 100 meters, surrounded by a circular fence. A goat is tied to a point on the fence with a chain. To prevent the goat from overeating, the farmer wants to ensure it can access only half of the grass in the field. What should be the length of the chain?
To clarify, the circular field represents the grassy area. The point S denotes where the chain attaches to the fence. The yellow section illustrates where the goat can graze, while the green section is out of reach for the goat. The objective is to determine the chain's length so that both the green and yellow areas have equal sizes.
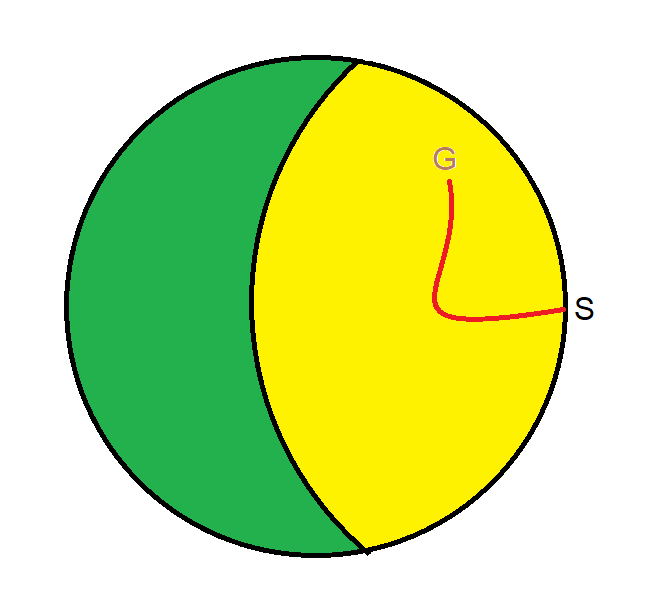
Please consult the accompanying diagram as you work through this problem.
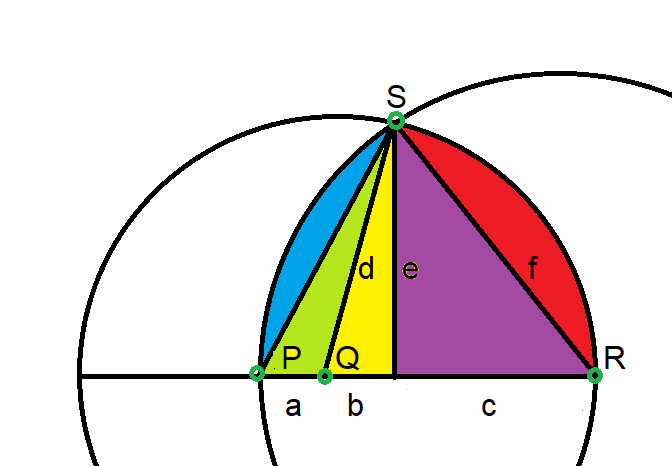
Point Q marks the center of the grassy circle. The goat's chain is secured to point R, allowing it to access all the shaded regions, including their reflections below line PR.
Since the radius of the grassy circle is 100, we have b+c = d = 100.
I will approach this problem by defining various elements in terms of b. Then, I will manipulate b until I achieve the condition that allows the goat to munch on half of the grass.
Let's begin by expressing e in terms of b. Examining the triangle formed by sides b, d, and e, we can apply the Pythagorean theorem:
b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = sqrt(10000 - b^2)
Now, let's determine f in relation to b. We know from earlier that b + c = 100, so c is equal to 100 - b. Applying the Pythagorean theorem:
c^2 + e^2 = f^2
(100-b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)
Next, we will calculate the area of triangle QRS:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
Following that, let's compute the area of the segment of the grassy field created by angle SQR:
tan(SQR) = e/b = sqrt(10000-b^2)/b.
slice SQR = atan(sqrt(10000-b^2)/b)
The area that is red consists of the segment SQR minus triangle QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).
Now, let's consider the combined area of blue, green, yellow, and purple regions. First, we must find the angle QRS.
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
angle QRS = atan(sqrt(10000-b^2)/(100-b)).
Adding the red area gives us half of the total area accessible to the goat:
atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).
We will double that to cover the area beneath line PR to achieve the total area:
2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).
The overall area of the grassy space amounts to 10,000*pi.
Finally, you will need to adjust b until you find an area for the goat that equals 5,000*pi. The goal-seek function in Excel is perfect for scenarios like this. I can't imagine how tasks were handled before the advent of spreadsheets.
By following this method, you will discover that b = 32.867402.
Consequently, we determine that the chain should be approximately 115.8728598 meters long.
This topic is being discussed in my forum at Wizard of Vegas .
What are the most commonly occurring two-letter combinations found at the start and end of five-letter words?
You must be asking because you enjoy Wordle . My answer is based on this list of 2,315 possible Wordle answers .
The following list showcases the most frequent combinations appearing as the first two letters.
First Two Letters
| Count | First Two Letters |
|---|---|
| 65 | ST |
| 52 | SH |
| 45 | CR,SP |
| 40 | CH |
| 38 | GR |
| 36 | FL,RE,TR |
| 35 | BR |
| 34 | MA |
| 32 | BL,CA |
| 31 | CL |
| 29 | CO,DR,MO,SC |
| 28 | DE,SL |
| 26 | BE,PR |
| 25 | PA |
| 24 | BA,TH |
| 23 | QU,RA,SA,SW,TA |
| 22 | AL,BO |
| 21 | FI,FR,LE,TO |
| 20 | BU,RO |
| 19 | HA,LO,PL |
| 18 | LA,PI,SN,UN,WH |
| 17 | DI,FO,HO,PO |
| 16 | FE,GL,GU,ME,PE,VI,WO |
| 15 | DO,GA,MI,PU,RI,SM,TE,WI |
| 14 | AB,FA,IN,LI,SE,SO |
| 13 | AN,BI,GO,HE,SI,SU,WA |
| 12 | AR,MU,TI,WR |
| 11 | AM,HU,LU |
| 10 | AD,AG,EL,EN,EX,FU,KN,NO,VA |
| 9 | CU,DA,DU,RU,SK,TW,VO,WE |
| 8 | AP,JU,NA,TU |
| 7 | AW,EA,GI,NE,NI,VE |
| 6 | AS,CI |
| 5 | AF,EM,ER,EV,GE,HI,ID,JO,OU,OV,US |
| 4 | AC,AU,AV,ET,HY,IM,JE,LY,OC,OP,PH |
| 3 | AT,AX,CE,CY,DW,KA,KI,NU,OF,OL,OR,SQ |
Among the combinations that appeared only once or twice, the following were not included in the main list.
- Appearing two times: AI, ED, EP, EQ, ES, GH, GN, IC, IR, IS, JA, NY, OD, OM, ON, OT, OW, RH, SY, UL, UP, UR, UT, YE, YO, ZE.
- Listed once: AH, AO, AZ, BY, DY, EB, EC, EE, EG, EI, EJ, EK, EY, FJ, GY, IG, IL, IO, IT, IV, JI, KE, KH, KO, KR, LL, MY, OA, OB, OX, OZ, PS, PY, TY, UD, UM, VY, YA, YI, ZO.
Here you will find the most common combinations among the last two letters.
Last Two Letters
| Count | Last Two Letters |
|---|---|
| 141 | ER |
| 58 | CH |
| 56 | LY |
| 52 | SE |
| 50 | AL |
| 47 | CK |
| 46 | TY |
| 39 | TE |
| 38 | DY,EL,GE,NG |
| 37 | NT,VE |
| 36 | ST,TH |
| 35 | LE |
| 34 | EN,OR |
| 33 | RY |
| 31 | KY |
| 30 | CE |
| 29 | ET |
| 28 | DE,NK |
| 27 | IC,NE,SH |
| 26 | ON,RE |
| 25 | ID,LL |
| 23 | ED,IT,NY |
| 22 | IN,ND |
| 21 | RT,SS |
| 20 | AR |
| 19 | IL,KE,ME,MP,SY,UT |
| 17 | LT |
| 16 | AT,PY |
| 15 | AN,UE |
| 14 | PE,RD,WN |
| 13 | AD,AY,EY,FF,MY,OT,RN |
| 12 | AK,GY,US |
| 11 | HT,LD,MA,ZE |
| 10 | EE,FT,PT,RA |
| 9 | CT,FY,GH,GO,OM,RK,UR |
| 8 | BY,OP,OW,WL |
| 7 | EP,HY,IE,IR,PH,TA,TO,UM,ZY |
| 6 | AM,BE,EW,HE,IO,OY,RM,RO |
| 5 | BO,CY,IA,LA,NA,OD,OL,RL,SK,UL,VY |
| 4 | AP,EF,EM,GN,IM,IP,LK,MB,OK,RP,UD,UP |
| 3 | AC,AW,DO,EK,EO,FE,GA,KA,LM,OF,RF,SM,SO,SP,TZ |
Among the combinations that appeared only once or twice, the following were not included in the main list.
- Appearing two times: AB, AX, BA, BI, CA, EX, HA, IF, IX, LO, LP, NO, OO, OS, OX, PO, UB, UG, UN, VA, VO, WY, XY, ZA.
- Listed once: AE, AH, AO, AZ, BT, CO, EA, GI, HI, HO, IB, IG, II, IK, IS, JA, JO, KI, KO, LF, LI, MI, MO, OA, OB, OC, OE, OU, PA, RB, RH, SA, SI, TI, UI, WD, XT, YL, YP, YR.


