Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Participate in slot tournaments offering enormous prize pools.
Ask The Wizard #355
In the film 'License to Kill,' James Bond engages in three rounds of blackjack, playing five separate hands simultaneously. Interestingly, he refrains from hitting on any of them. What are the chances of such an occurrence?
You may find a clip of the scene on YouTube .
It does appear that a disproportionately large number of high-value cards are dealt during the game. Here are the cards I managed to identify, although some were not clearly visible.
License to Kill -- Ranks Observed
| Rank | Observed |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| J | 3 |
| Q | 6 |
| K | 4 |
| A | 1 |
| Total | 35 |
You're absolutely correct; Bond does not hit on any of his initial 15 hands. He does split a pair of eights once, but again, he refrains from hitting afterward. Here's a breakdown of his actions with all 15 hands:
- Double — 1
- Split — 1
- Stand — 13
The following are the basic strategy probabilities associated with his initial moves, assuming a six-deck shoe, the option to double after a split, the dealer checking for a hole card, and standing on a soft 17.
Probabilities of the First Action in Blackjack
| Action | Probability |
|---|---|
| Stand | 43.46% |
| Hit | 39.78% |
| Double | 9.53% |
| Split | 2.48% |
| Blackjack | 4.75% |
| Total | 100.00% |
If players had the option to surrender, the probability of doing so would be 4.14%, taken from the likelihood of standing.
It's worth mentioning that Bond stood on a 16 against a dealer's 10. The typical strategy suggests hitting in that situation, but it's a close call. Considering the series of tens that appeared during that round, Bond may have been aware of a high count, which would justify his decision to stand.
The likelihood of not hitting on any given hand is 60.22%. The chance of not hitting on all 15 hands, assuming each one operates independently, is 0.602162.15= 0.000496253 = apx. 1 in 2015.
In the series 'The Squid Game,' 16 contestants face the perilous challenge of crossing a bridge made of glass. The bridge consists of 18 pairs of glass panels, with one tempered glass piece capable of supporting a player's weight in each pair. The other panel is regular glass that will shatter if someone steps on it. Falling through an ordinary glass panel would lead to their demise.
Contestants must proceed in a specific order, one at a time.
If we assume that players are guessing randomly at each set of glass panels, what would be the average number of players expected to cross successfully?
I will conceal the answer and solution within spoiler tags, allowing others to enjoy finding the answer for themselves.
The probability of player 1 crossing safely is calculated as (1/2)^18 = 1/262144, which is approximately 0.000004.
Player 2 has the following two options to cross safely:
- If player 1 successfully crosses, player 2 can simply follow in their footsteps.
- Between player 1 and player 2, there is only one incorrect step possible. This could occur at any of the 18 pairs of glass. Therefore, the probability of having 17 correct steps and one incorrect step is 18*(1/2)^2 = 18/262144, which is about 0.000069.
Thus, the probability of player 2 crossing safely is the sum of these two outcomes: 0.000004 + 0.000069 = 0.000072.
Player 3 has two methods to cross safely:
- If player 2 crosses without issue, player 3 can mimic their steps.
- Among players 1, 2, and 3, there are only two incorrect steps possible. The combinations of selecting 2 from 18 pairs of glass result in combin(18,2)=153 ways for two glass panels to cause the demise of players 1 and 2. The probability of having 16 correct steps and two incorrect steps is 153*(1/2)^2 = 153/262144, resulting in approximately 0.000584.
The probability of player 3 crossing safely is, therefore, 0.000072 + 0.000584 = 0.000656.
Player 4 can cross safely in two ways:
- Should player 3 cross without issues, player 4 can replicate their steps.
- For players 1 through 4, there are three potential missteps. The number of ways to select 3 pairs of glass from 18 is given by combin(18,3)=816, which accounts for the two pieces that could endanger the first three players. The likelihood of 15 correct steps and three incorrect ones is 816*(1/2)^2 = 816/262144, equating to roughly 0.003113.
Following this reasoning, we can compile the following probability table for each player.
Bridge Game
| Player | Probability Survival |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 13 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| Total | 7.000076 |
To present the answer in a concise form, it would be:
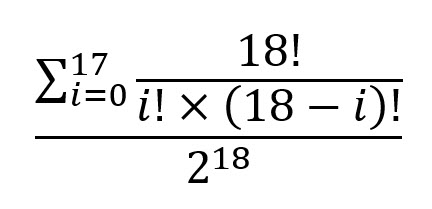
In an intriguing discussion brought up in my forum, at the 3:10 mark, you receive a complete full house, specifically threes over fours. The multiplier for four-of-a-kind between twos and fours was set at 9x, while a full house had a multiplier of 1x. Could you explain why you opted to keep the full house instead of discarding it for just the three 3s to try and achieve the four-of-a-kind at a better multiplier? Wizard of Vegas .
In your Ultimate X Gold You're spot on; I definitely made an error with that hand.
Keep in mind, I was playing 10-play. Therefore, my winnings with the full house amounted to 10×35 = 350.
When holding only the threes, each hand had its corresponding probabilities:
Here are the winnings for each hand after accounting for the multipliers:
- Four of a kind — 4.26%
- Full house — 6.11%
- Three of a kind — 89.64%
My expected return with just the threes would have been calculated as (4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854. This is significantly more than the mere 35 from the full house. Therefore, yes, I made a rather embarrassing blunder with that hand.
- Four of a kind — 1800
- Full house — 35
- Three of a kind — 15
Someone presented me with the following wager. I would select any three ranks from a standard poker deck, noting my prediction, but keeping it hidden until the end. For instance, I might choose 7-ace-2. They then bet me even money that they could name at least one of my chosen ranks if given three guesses. What were my chances of winning?
To win, your opponent must be incorrect with all three guesses. The odds of getting the first guess wrong are 10/13. For the second guess, the chance of being wrong increases to 9/12, as the first rank guessed is no longer a possibility. Lastly, the third guess has an 8/11 chance of being incorrect, as the first two guessed ranks are excluded from consideration.
All of these events need to occur for you to be victorious. Hence, your chances of winning can be calculated as (10/13) * (9/12) * (8/11) = 720/1716, which is around 41.96%.
Given the even payout, the house edge based on this wager from your perspective is 16.08%, which is rather steep.
This scenario was referenced in 'The Book of Proposition Bets' by Owen E'Shea (item 7).
Correct mathematical strategies and valuable insights for casino games like blackjack, craps, roulette, and many others that can be played.