Ask The Wizard #353
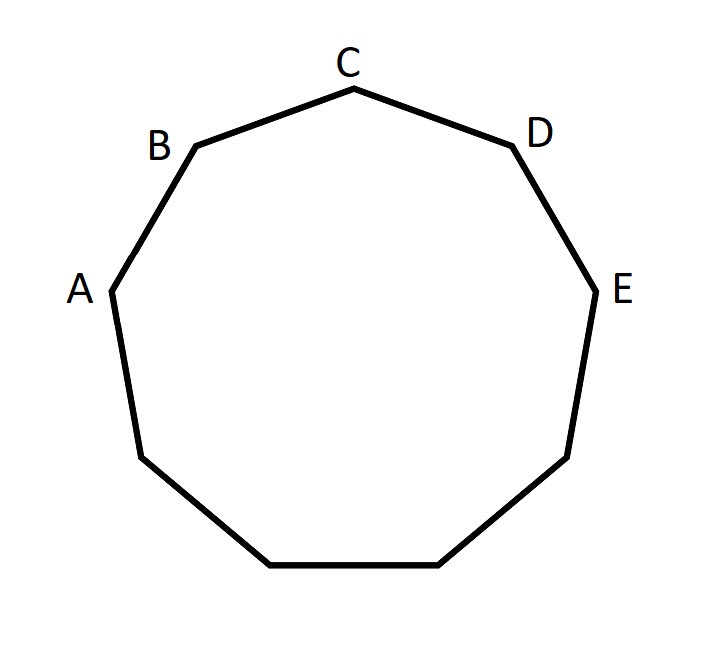
The shape illustrated is a nonagon, characterized by having sides of equal length, each measuring one unit.
Which is more, AB+AC or AE?
This particular question was sourced from the Mensa Bulletin published in March 2021.
Here is my solution to this problem. (PDF)
What are some straightforward methods to determine the square root of any number that has three or four digits, assuming the outcome is an integer?
The next table details the numbers from 0 to 9, their squares, and the last digit of each square.
Last Digit of Square Numbers
| Original Number |
Square | Last digit of Square |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
It's essential to observe that even-numbered squares always conclude with the digits 0, 1, 4, 5, 6, or 9, a rule that holds true for all square numbers. The last digit of the base number dictates the last digit of its square.
Step 1: By examining the last digit of the square, you can consult the corresponding table to deduce the last digit of the square root. For instance, if the square is 2809, its square root ends in either 3 or 7.
Last Digit of Original Number
| Last digit of Square Root |
Last digit of Square |
|---|---|
| 0 | 0 |
| 1 | 1 or 9 |
| 4 | 2 or 8 |
| 5 | 5 |
| 6 | 4 or 6 |
| 9 | 3 or 7 |
Step 2: Next, take the original number and discard the last two digits. For example, with the number 2809, you would consider only 28.
Step 3: Identify the largest square number that is equal to or less than the result from Step 2, and then compute its square root. For instance, the largest square less than 28 is 25, whose square root is 5.
If you haven't memorized the squares up to 100, refer to the following table for assistance.
First Portion of Square Root
| Step 2 | Step 3 |
|---|---|
| 1 to 3 | 1 |
| 4 to 8 | 2 |
| 9 to 15 | 3 |
| 16 to 24 | 4 |
| 25 to 35 | 5 |
| 36 to 48 | 6 |
| 49 to 63 | 7 |
| 64 to 80 | 8 |
| 81 to 99 | 9 |
Step 4: If the outcome from Step 1 is either 0 or 5, simply append this to the result from Step 3, and you will have your final answer.
If the value isn't 0 or 5, define a as the output from Step 3, and determine b using the formula a multiplied by (a plus one). For example, if Step 3 gave you 5, then b would be calculated as 5 multiplied by 6, resulting in 30.
Step 5: If b is less than a, then pick the smaller last digit from Step 1. If b is equal to or greater than a, use the larger option.
Step 6: To finalize the square root, combine the result from Step 3 with that from Step 5 using the formula 10 multiplied by the result from Step 3 plus Step 5.
Let's look at some examples:
Find the square root of 256.
- Step 1: The possible last digits of the square root are either 4 or 6.
- Step 2: Dropping the last two digits, we get 2.
- Step 3: The largest square that does not exceed 2 is 1, and the square root of 1 is 1.
- Step 4: 1*(1+1) = 2.
- Step 5: The output of Step 4 matches that of Step 2, so we take the greater option from Step 1, which is 6.
- Step 6: Thus, the square root emerges as the result from Step 3, combined with that from Step 5, leading to 1 and 6, which results in 16.
Find the square root of 1369.
- Step 1: The last digit of the square root can either be 3 or 7.
- Step 2: Dropping the last two digits, we get 13.
- Step 3: The highest square less than or equal to 13 is 9, hence the square root of 9 is 3.
- Step 4: 3*(1+3) = 12.
- Step 5: Since the result from Step 2 exceeds that of Step 4, we opt for the higher choice from Step 1, which is 7.
- Step 6: Consequently, the square root is represented by the outcome from Step 3 and Step 5, giving us 3 and 7, resulting in 37.
Find the square root of 2704.
- Step 1: The last digit of the square root may be either 2 or 8.
- Step 2: Dropping the last two digits, we get 27.
- Step 3: The highest square that remains under or equal to 27 is 25, whose square root is 5.
- Step 4: 5*(1+5) = 60.
- Step 5: The result from Step 2 is lower than that of Step 4, so we select the smaller option from Step 1, which is 2.
- Step 6: Therefore, the square root combines the findings from Step 3 and Step 5, producing 5 and 2, resulting in 52.
Find the square root of 5625.
- Step 1: The last digit of the square root is identified as 5.
- Step 2: Dropping the last two digits, we get 56.
- Step 3: The largest square that doesn’t exceed 56 is 49, and the square root of 49 is 7.
- Step 4: Since the result from Step 1 is either 0 or 5, your answer will be formed by adding the value from Step 3 with that from Step 1, which gives 7 and 5 resulting in 75.
Find the square root of 6561.
- Step 1: The last digit is 1 or 9.
- Step 2: Dropping the last two digits, we get 65.
- Step 3: The greatest square that is less than or equal to 65 is 64, whose square root is 8.
- Step 4: 8*(1+8) = 72.
- Step 5: The result from Step 2 falls short of that from Step 4, a reason to adopt the smaller final digit from Step 1, which is 1.
- Step 6: Hence, the square root consists of the outcome from Step 3 combined with that from Step 5, leading to 8 and 1, resulting in 81.
You can find an example illustrating this technique on YouTube .
In a duration of 12 hours spent playing blackjack, what are the chances of achieving 60 or more consecutive wins?
According to my variance in blackjack based on generous Strip rules, the following outlines the probabilities of achieving a net gain, a tie, or a loss:
- Win — 42.43%
- Push — 8.48%
- Loss — 49.09%
If we set aside the ties, we have a probability of winning, considering outcomes resolved in a net win or loss, sitting at 46.36%.
Let's assume you play 100 hands in an hour at a consistent pace.
We can estimate the likelihood of observing at least one winning streak of 60 hands in succession as:
100×12×0.463660= 1 in 89,412,355,233,588,500.For comparison’s sake, if you were to buy one Powerball ticket along with one Megamillions ticket, the odds of winning both would be approximately 1 in 88,412,922,115,818,300.
Thus, it turns out to be slightly more feasible to win both lotteries than it is to experience 60 wins consecutively during 12 hours of play.


