Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Participate in Slot Tournaments with Enormous Prize Pools
Ask The Wizard #351
How effective do you find this approach to playing roulette?
- Bet two units on black
- Bet one unit on the third column
This strategy shines because there are 8 red numbers and 4 black numbers located in the third column. Out of the total 16 red, half fall within the first two columns while the other half lies in column three. For the moment, let's disregard the 0 and 00 on the wheel. When the ball lands on a red number, 8 out of the 18 options available are located in the third column. This gives a winning probability of 8/18, and since the winnings are paid at odds of 2 to 1, the player has a 33.3% advantage. Even if we factor in even betting on black which has a house edge of 0%, and ignoring the 0 and 00 for the time being, the player advantage still amounts to 16.7%. Once we do include the potential 0s, my calculated advantage turns into (2/38)*-100% + (36/38)*16.7% = 10.53%! What are your thoughts on this?
I concur that the conditional edge of betting on the third column is indeed 33.3%, considering the ball falls on red while ignoring both zeros. However, applying the same rationale, if the ball were to hit black, the probability of winning with a bet on the third column drops to 4/18 or 2/9. A 2/9 chance of winning with a payout ratio of 2 to 1 carries an equivalent house advantage of 33.33%. Thus, if viewed from your standpoint, the third column wager offers a 33.33% player advantage half the time but also has a house edge of 33.33% for the other half, effectively negating each other and resulting in a 0% house edge overall. However, when we factor in the presence of the two zeros, the total player edge adjusts to (2/38)*-100% + (36/38)*0% = -5.26%.
Taking a different perspective, the following table illustrates the potential outcomes as well as their respective probabilities, wins, and contributions to returns. The bottom right corner denotes an anticipated loss of -0.105263 units, which when divided by the 2 units wagered, reveals a house edge of 5.26%.
Bohemia Strategy
| Event | Pays | Numbers | Probability | Return |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0.052632 | -0.105263 |
| Red & column 1 or 2 | -2 | 10 | 0.263158 | -0.526316 |
| Red & column 3 | 1 | 8 | 0.210526 | 0.210526 |
| Black & column 1 or 2 | 0 | 14 | 0.368421 | 0.000000 |
| Black & column 3 | 3 | 4 | 0.105263 | 0.315789 |
| Total | 38 | 1.000000 | -0.105263 |
In casinos throughout Las Vegas, the colors assigned to chips for values of $100 and less are widely recognized, as follows:
- $1 = White or blue
- $5 = Red
- $25 = Green
- $100 = Black
However, I'm curious to know what colors are designated for chips valued over $100?
Generally, the color purple is used for $500 chips while yellow is reserved for $1,000. Above this threshold, there isn't a universal standard. While orange and brown are frequently seen, this isn't a rule set in stone since not all establishments adhere to this practice. Occasionally, you'll see white and blue chips making a comeback. It’s worth mentioning that those colors were previously used for $1 chips, yet at higher bets like the $1,000 chips, the size of the chips changes. The following table summarizes what I've been able to ascertain.
Chip Colors
| Casino | $5,000 | $25,000 | $100,000 |
|---|---|---|---|
| Resorts World | Brown | Orange | |
| Cosmopolitan | White | Orange | |
| Treasure Island | White | ||
| Palazzo/Venetian | Brown | Orange | Grey/brown |
| Green Valley Ranch | Brown | ||
| Circa | Orange | ||
| Wynn | White/red | Brown | |
| Bellagio | White | Orange | Steel blue |
| Golden Nugget | Red, white and blue |
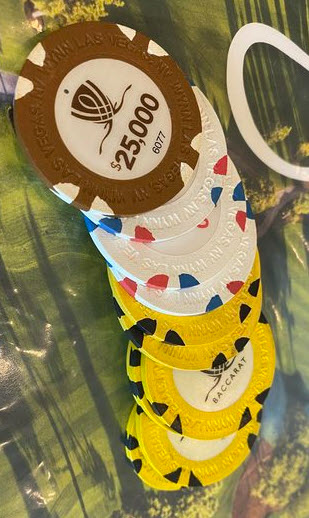
I extend my gratitude to Mdawg for his assistance with this inquiry and for providing the images.
This topic has been brought up and is being discussed in my forum at Wizard of Vegas .
Did you catch that video featuring a player who astutely predicted the flop, turn, and river in a game of Texas Hold 'Em? What are the odds of such an occurrence?
During the flop, the player confidently calls out 8-9-10, without specifying any suits. All they know is that they folded a jack and queen. The possible combinations for 8, 9, and 10 to show up on the flop total to 4*4*4 = 64. With 50 unknown cards still in the deck, the total combinations for choosing three cards from the remaining 50 are described by combin(50,3) = 19,600. Therefore, the likelihood of hitting the correct flop is calculated as 64/19,600, translating to 1 in 306.25.
When it comes to the turn, there are now 47 unknown cards left. The player successfully identifies the four of spades, which had a probability of 1 in 47 to hit.
On the river, the player correctly predicts the two of hearts from the remaining 46 unknown cards, which had a 1 in 46 shot.
To compute the overall probability of making all three correct predictions, the formula is (46/19600) × (1/47) × (1/46) = 1 in 662,113.
As far as my personal view goes, it seems to be pure luck. I've seen so many incorrect predictions at the gaming tables that it's quite common. Do you really think anyone highlights the countless false predictions in YouTube videos that quickly fade into obscurity? In light of that, my reaction is one of indifference.