Wizard Recommends
100 % up to
2250zł +200 spins- Massive gaming platform
- Crypto-friendly
- Loyalty program
120 % up to
1200zł +50 spins- Welcome bonus package
- Loyalty Program
- Exciting slot tournaments with huge prize pools.
Ask The Wizard #338
What is the typical number of rolls required using two dice to achieve every possible total from 2 to 12?
While utilizing a Markov chain is one way to tackle this question, I prefer leveraging calculus. The important point to note is that the result remains consistent if the time intervals between rolls follow an exponential distribution with a mean of one. Hence, the answer can be expressed as the integral from 0 to infinity of:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6)).
Integrals of this nature can be easily computed using an integral calculator .
Any of these problems can also be resolved using my Expected Trials Calculator .
Imagine an ant positioned exactly in the center of a square. It is situated 17 inches away from the upper-left corner, 20 inches from the upper-right corner, and 13 inches from the lower-right corner.
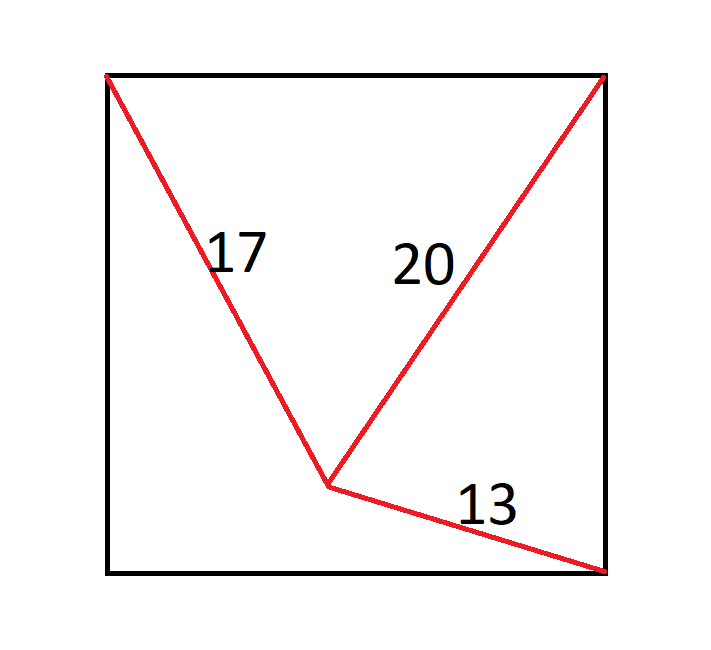
How large is the square?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
To begin, rotate triangle ABE by 90 degrees to create a new triangle labeled BDF.
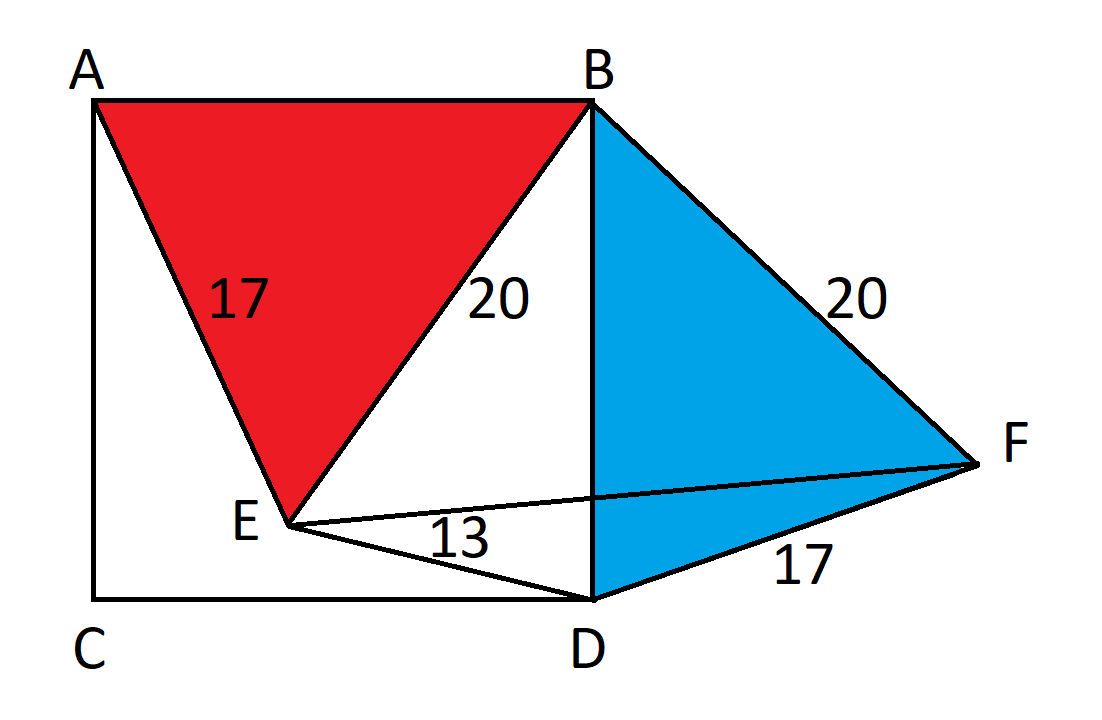
Because triangle ABE was rotated by 90 degrees, angle EBF is defined as 90 degrees. According to the Pythagorean theorem, EF is calculated as 20 times the square root of 2.
Applying the law of cosines gives us: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
Remember that sin^2(x) + cos^2(x) equals 1. Let's utilize this identity to determine sin(DEF).
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
Next, consider angle BED.
Angle BED = Angle BEF + Angle FED.
Since EBF measures 90 degrees and forms an isosceles triangle, it follows that angle BEF must measure 45 degrees.
So, Angle BED = 45 degrees + Angle FED.
Recall, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
We can express cos(BED) as cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED).
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Now, we will apply the law of cosines to triangle BED once more.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD represents one side of the square under consideration, so BD^2 will yield the area of that square, which we have already established to be 369.
This topic is discussed within my forum at Wizard of Vegas .
Drop Dead is an engaging game that utilizes five standard dice. At the start of your turn, you roll all five dice. If none of the dice show a 2 or a 5, you sum the values and add that total to your score before rolling again. However, if you roll any dice showing a 2 or 5, your score for that turn becomes zero. Any dice that show a 2 or 5 are considered inactive and set aside. You proceed to roll again with the remaining dice. The gameplay continues in this manner, where you either accumulate points or eliminate dice. Your turn concludes when all of your dice have been set aside, at which point you are said to have 'dropped dead.' Ultimately, your total score is the sum of all your successful rolls, and the player with the highest score wins.
What is the expected score you would anticipate achieving in this game?
Let’s analyze the situation when there is only one die remaining and work backward from there.
We'll denote the variable 'a' as the expected additional points when just one die remains.
The average outcome for a roll that does not result in a 2 or 5 is calculated as (1+3+4+6)/4 = 7/2.
a = (2/3)×(a + 7/2).
a/3 = 7/3.
a = 7.
Next, let's determine 'b,' which represents the anticipated points when there are two dice left.
b = (2/3)2×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11.2.
Now, moving on, we'll calculate 'c,' representing the expected points with three dice still in play.
c = (2/3)3×(c + 3× (7/2)) + 3×(2/3)2×(1/3)×b + 3×(2/3)×(1/3)2×b.
c = 1302/95 = 13.705263.
Next up is calculating 'd,' the expected points when you have four dice left.
d = (2/3)4×(d + 4× (7/2)) + 4×(2/3)3×(1/3)×c + 6×(2/3)2×(1/3)2×b + 4×(2/3)×(1/3)3×a.
d = 3752/247 = 15.190283.
Lastly, let's find 'e,' which signifies the expected points remaining when all five dice are still in action.
e = (2/3)5×(e + 5×(7/2)) + 5×(2/3)4×(1/3)×d + 10×(2/3)3×(1/3)2×c + 10×(2/3)2×(1/3)3×b + 5×(2/3)×(1/3)4×a.
e = 16.064662.
This topic is discussed within my forum at Wizard of Vegas .
Take into account the Pairplus wager in Three Card Poker, which adheres to the 1-4-6-30-40 payout structure. Interestingly, this wager features a jackpot for a mini-royal in spades and grants 25% of that jackpot for mini royals in the other three suits. How elevated must the meter be for this bet to be deemed fair?
The answer is 384 times the bet amount.
With every additional 100 bets beyond that threshold, the payout percentage increases by 0.79%.
This topic is discussed within my forum at Wizard of Vegas .