Ask The Wizard #323
Is this parlay card any good?

To begin, you must place a wager on either side against the spread in an NFL game. As of January 2, 2020, the Vikings were the underdogs by 7.5 points. Based on my calculations from the NFL alternate point spread calculator, the likelihood of the Vikings at +8.5 successfully winning that match is 52.22%. For the other games I've analyzed, I reviewed the current money lines, adjusted for the juice, to calculate the winning probabilities. The table below illustrates the probability for each selection.
In step one, the two selections with the highest chances of winning are the Patriots and LSU. Here’s the winning probability for my suggested choices:
William Hill Parlay Card
| Leg | Fair Wine | Prob. Win |
|---|---|---|
| Saints -8.5 | -7.5 | 47.78% |
| Vikings +8.5 | 8.5 | 52.22% |
| Hou | -135 | 57.45% |
| Bills | 135 | 42.55% |
| Patriots | -205 | 67.21% |
| Titans | 205 | 32.79% |
| Sea | -118 | 54.13% |
| Phil | 118 | 45.87% |
| LSU | -200 | 66.67% |
| Clemson | 200 | 33.33% |
| AFC | -130 | 56.52% |
| NFC | 130 | 43.48% |
The combined probability for these outcomes stands at 23.40%. Betting at 4 to 1 yields a return of 4 × 23.40% = 93.60%. This indicates that the house advantage is 6.40%, so I would recommend avoiding this bet.
- Vikings +8.5 — 52.22%
- Patriots — 67.21%
- LSU — 66.67%
I'm considering introducing a side bet for 'push 22' variants in blackjack that would pay out at 11 to 1 if the dealer busts with a hand of 22. What would the odds be?
I'm thinking of launching a side bet for 'push 22' Blackjack variants that wins if the dealer busts with a hand totaling 22. What payout should it offer, and what would the house edge look like?
If we assume the dealer always completes their hand (even if all players have busted), then the odds of busting on 22 stands at 7.88% when the dealer stands on a soft 17 and 8.00% if they hit on a soft 17.
If the dealer hits a soft 17 and the payout is set at 11 to 1, the house edge would be calculated at 4.04%. However, at a 10 to 1 payout, this edges up to 12.04%.
It's important for me to alert players that this strategy is countable (quiet, Wiz!).
In a contest between Amy and Bob to be the first to achieve four wins in flipping a fair coin, Amy intends to wager $8,000 on her winning. However, she can only place bids on one flip at a time. All bets are at even money. How should she organize her wagers to ensure she gains $8,000 if she wins overall and loses $8,000 if Bob comes out on top?
Press the button below for the solution.
There are 16 potential states during the series. The table below outlines the optimal bet for Amy to make at each state and her balance prior to placing that bet according to this strategy.
Hit the button below to view the answer.
Answer
| Amy | Bob | Balance | Bet |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
In such puzzles, a sound strategy is to work from the end back to the beginning. That said, it becomes evident that:
Let:
- a = Amy wins
- b = Bob wins
- w = Amy's net win so far in series
- f(a,b,w) = Amy's bet size next game
In this scenario, the seventh game becomes 'winner takes all.' Amy should start with zero winnings and place an $8,000 bet on the final coin flip, which will result in her winning $8,000 if she wins and losing $8,000 if she does not.
f(3,3,0) = 8,000
Looking back a step, suppose she has 3 wins and Bob has 2. If she wins the next flip, she secures the entire game. However, if she loses, the score will tie at 3-3. From f(3,3,0), she should aim for a balance of 0 when the score is tied at 3-3. Therefore, she needs $8,000 if she wins the next flip and $0 if she does not. To achieve this, an interim win of $4,000 with a matching bet will suffice. Thus:
Taking another step back, assume she has 3 wins while Bob has only 1. Winning the next flip means she wins the game, while losing it would bring the score to 3-2. From f(3,2,4000), she should have $4,000 at a 3-2 score. Hence, she requires $8,000 if she wins and $4,000 if she loses. To get to this setup, an interim win of $6,000 and betting half of the difference between those amounts, which is $2,000, is necessary. Therefore:
f(3,2,4000)=4,000
Now, consider the next step back, where she has 3 wins and Bob has no wins. A victory on the next flip means she wins the game, whereas a loss will place the score at 3-1. The outcome from f(3,1,6000) shows she ought to have $6,000 at a 3-1 score. As such, she needs $8,000 for a win and $6,000 for a loss. An interim win from the difference gives us $7,000 and a bet of $2,000 gets her to the desired points. So:
f(3,1,6000) = 2,000
It's clear that Amy should maintain a net win of 0 when the scores are even. In any tied scenario, her overall probability of winning the entire match stands at 50%. With the balanced goal of $8,000 whether she wins or loses, she needs to keep her bets at $0, or she risks missing both goals.
f(3,0,7000) = 1,000
Furthermore, if Amy falls behind in the standings, her net win should be the opposite of what it would be if she were leading by the same margin. For instance, take the score of Amy 2, Bob 3. If she loses the next flip, she loses the overall game. Yet, winning that flip brings her to a tie at 3-3. From f(3,3,0), she should be at $0 with a 3-3 score. Thus, she should aim for $0 with a win and -$8,000 with a loss. This scenario presents a net loss of $4,000 with a bet matching that amount. Therefore:
Now, what about Amy's wager if the score is at 2-2? Winning the flip brings the score to 3-2. Referring back, we see that she should have a net gain of $4,000 at that score. Additionally, we know that if she is down 2-3, a net loss of $4,000 is essential. Consequently, her bet should be set at $4,000.
f(2,3,-4000)=4,000
By the same logic:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
Stepping back further, consider the score at 2-1. We noted she needs a net win of $6,000 if she wins the next flip (resulting in a 3-1 score) and $0 if she doesn’t (tying it at 2-2). To balance this, she would require a net win of $3,000 as a midpoint, thus her bet should be $3,000.
f(2,2,0) = 4,000
In another preceding step, what if she stands at 2 wins to Bob’s 0? Winning the next flip secures a 3-0 score, while a loss would lead to 2-1. She should target $7,000 when at 3-0 and $3,000 at 2-1. This would call for a net win from 2-0 to average out at $5,000, with a corresponding bet of $2,000.
f(2,1,3000) = 3000
By turning the scores around whereby Amy holds two victories and Bob has less, we can conclude:
f(2,0,5000) = 2000
As noted earlier, Amy's net win must equal 0 when the series is level. Therefore, at a score of 1-1, her net win also equals 0. With a score of 2-1, she aims for a 2,000 lead, while at 1-2 she faces a 2,000 deficit. Thus, at a score tied at 1-1, her ideal bet would be $2,000, meaning:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
Suppose Amy leads 1-0. We established she should be ahead by 5,000 at a score of 2-0. When at 1-1, she should break even. To progress from 1-0, a net win of $2,500 is achieved, as well as a betting difference of $2,500.', "Finally, we arrive at the starting game with the score at 0-0. Amy needs to maintain a $2,500 positive win if she wins the following flip, or a $2,500 loss if she loses. Recognizing this, a bet of $2,500 sets the stage for her.
f(1,1,0) = 2,000
This topic has been raised and is open for discussion in my forum at
f(1,0,2500) = 2,500
By flipping the score to 0-1:
f(0,1,-2500) = 2,500
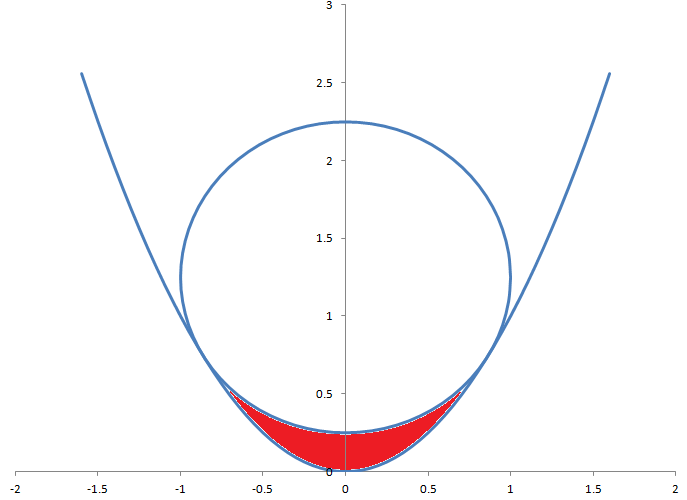
A circle with a radius of 1 touches the parabola defined by the equation y=x. What is the calculated area of the red region located between the circle and the parabola?
f(0,0,0) = 2,500
This topic is brought forth and discussed in my forum at Wizard of Vegas .
I encountered this challenge from Presh Talwalker from2Providing mathematically sound strategies and information for various casino games, including blackjack, craps, roulette, and numerous others available for play.
There are 16 potential states during the series. The table below outlines the optimal bet for Amy to make at each state and her balance prior to placing that bet according to this strategy.
Here is my solution . (PDF)
Please check your inbox and click the link we sent to finalize your registration. Wizard of Vegas .
Explore the top online casinos available in your region. Mind Your Decisions .


