WOO logo

Wizard Recommends

  • Casino Infinity
    100 % up to
    2250zł +200 spins
    • Massive gaming platform
    • Crypto-friendly
    • Loyalty program
    Read Review
  • HellSpin Casino
    100 % up to
    400zł +100 spins
    • Bitcoin-friendly
    • Extra spins
    • Regular freebies
    Read Review
  • Verde Casino
    120 % up to
    1200zł +50 spins
    • Welcome bonus package
    • Loyalty Program
    • Slot competitions that feature substantial prize pools
    Read Review

Ask The Wizard #321

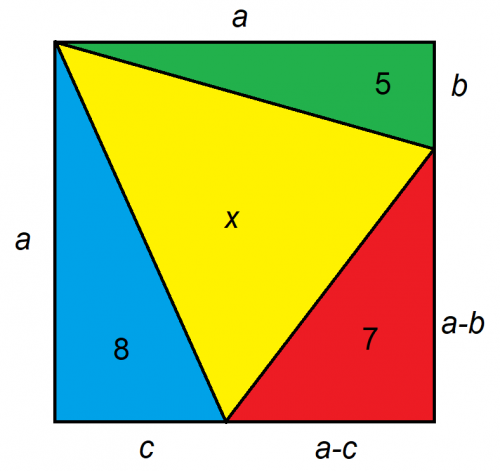
If we consider the larger figure as a square, can you calculate the area represented by x?

Dyana from Las Vegas

When tackling problems like this one, the key lies in how you set them up. It's advisable to simplify the situation to focus on the fewest unknowns possible. In this scenario, we can reduce the unidentified distances within the square to just three variables as follows:

four triangles in a square solution

Handling rectangles is generally simpler than dealing with triangles. Since we are aware of the areas of three triangles, we can double their dimensions along with their respective areas, which results in:

  • ab=10
  • ac=16
  • (a-b)(a-c)=14

Let's factor (a-b)(a-c):

a2- ab- ac + bc = 14

a2- 10 - 16 + bc = 14

(1) a2+ bc = 40

Let’s redefine variables b and c in terms of a to simplify our equation to a single variable:

b = 10/a

c = 16/a

Now, let’s replace b and c with their corresponding values in equation (1):

a2+ (10/a)*(16/a) = 40

a2+ 160/a2= 18

Next, let's get rid of that a2This involves multiplying everything in the denominator by a2.

a4+ 160 = 40*a2

a4- 40*a2+ 160 = 0

Let's define a new variable y = a2

y2- 18y + 32 = 0

Next, we'll apply the quadratic formula to find y:

y = (40 +/- sqrt(1600-640))/2

y = (40 +/- sqrt(960))/2

y = (40 +/- 8*sqrt(15))/2

y = 20 +/- 4*sqrt(15)

The area of the entire square is a2This conveniently simplifies to y. According to the previous equation, if we take the negative of the +/-, we find that y equals approximately 4.5081. This value seems unrealistic since we know that the area must be at least 20, without factoring in x. Hence, the area of the square should indeed be 20 plus 4 times the square root of 15.

The three triangles presented have total areas amounting to 5, 7, and 8, which totals 20. Subtracting this from the total area of the square leaves us with the area of x: 20 plus 4 times the square root of 15, minus the 20, which simplifies to 4 times the square root of 15, approximately equal to 15.4919.

This inquiry is a topic of discussion in my forum at Wizard of Vegas .

suncoast

Take a look at my t-shirt in this image. The cashier at the movie theater complimented it when I attended a screening of Uncut Gems . To express my gratitude, I presented her with a challenging problem involving triangles with areas of 2, 3, and 4. After the film, I checked on her progress, and while she hadn’t solved it yet, she seemed to be putting in effort. So, I wrote down a solution for her at the Suncoast bar. Interestingly, she seemed to value the effort, and I believe she has a bright future ahead.

Concerning the lottery, is there a specific jackpot amount in multi-state lotteries (like Powerball or Mega Millions) at which point it becomes more likely for the big prize to be shared among several winners rather than awarded to a single individual? If so, what would that figure be?

Ayecarumba from California

I won’t delve into all the mathematical intricacies, but here are the jackpot thresholds where having multiple winners becomes as likely as having just one:

  • PowerBall: $975 million
  • Mega Millions: $1.65 billion

Although you didn’t request it, here are the jackpot amounts where the likelihood of at least one winner matches the chance of no winners at all (50%).

  • PowerBall: $704 million
  • Mega Millions: $867 million

This question is a subject of discussion in my forum at Wizard of Vegas .

  • In the jail, there are 12 inmates who are numbered from 1 to 12.
  • The warden arranges 12 boxes, each assigned a number from 1 to 12.
  • Within these 12 boxes are the numbers 1 through 12, placed randomly with one number in each box.
  • Each inmate, in turn, will have the opportunity to open six boxes of their choice, doing so one at a time.
  • The objective for each prisoner is to locate their own assigned number inside one of the six boxes they selected. If they succeed, that inmate is said to have survived.
  • If an inmate fails to find their number, the entire group faces failure and will be led to a firing squad immediately.
  • If a prisoner survives, they are required to return the numbers back to their original boxes for the next inmate's turn.
  • Inmates are not allowed to observe others or communicate once the task begins.
  • Before starting, the entire group has the opportunity to devise a collective strategy. The primary goal is for all 12 inmates to survive, meaning each must find their own number in a box.

What strategy should they adopt to maximize their chances of survival, and what is that success rate?

anonymous

Utilizing the strategy laid out in the solution, the survival probability is calculated to be 166112640/479001600, which is approximately 34.68%.

Every prisoner’s initial choice should be their assigned number. If that number is found, they survive. If it isn’t, they then open the box that corresponds to the number they found in the first box. This process continues until they either find their number or have opened six boxes.

Similar to a Secret Santa event, a series of loops will emerge linking one number to another. For 12 prisoners, there can be anywhere from 1 to 12 loops. If there are no loops longer than six, every prisoner will eventually discover their number. The critical question becomes: what is the chance that no loop exceeds six in length? Let's approach this from the opposite angle and calculate the combinations for loops of size 7 or greater.

12 Prisoner Solution

Loops Combinations Probability
12 39,916,800 0.083333
11,1 43,545,600 0.090909
10,2 23,950,080 0.050000
10,1,1 23,950,080 0.050000
9,3 17,740,800 0.037037
9,2,1 26,611,200 0.055556
9,1,1,1 8,870,400 0.018519
8,4 14,968,800 0.031250
8,3,1 19,958,400 0.041667
8,2,2 7,484,400 0.015625
8,2,1,1 14,968,800 0.031250
8,1,1,1,1 2,494,800 0.005208
7,5 13,685,760 0.028571
7,4,1 17,107,200 0.035714
7,3,2 11,404,800 0.023810
7,3,1,1 11,404,800 0.023810
7,2,2,1 8,553,600 0.017857
7,2,1,1,1 5,702,400 0.011905
7,1,1,1,1,1 570,240 0.001190
Total 312,888,960 0.653211

The following table illustrates the formulas for the combinations shown in the table above.

Combination Formulas

Loops Combinations Formula
12 39916800 =FACT(11)
11,1 43545600 =COMBIN(12,11)*FACT(10)
10,2 23950080 =COMBIN(12,10)*FACT(9)
10,1,1 23950080 =COMBIN(12,10)*FACT(9)
9,3 17740800 =COMBIN(12,9)*FACT(8)*FACT(2)
9,2,1 26611200 =COMBIN(12,9)*COMBIN(3,2)*FACT(8)
9,1,1,1 8870400 =COMBIN(12,9)*FACT(8)
8,4 14968800 =COMBIN(12,8)*FACT(7)*FACT(3)
8,3,1 19958400 =COMBIN(12,8)*COMBIN(4,3)*FACT(7)*FACT(2)
8,2,2 7484400 =COMBIN(12,8)*COMBIN(4,2)*FACT(7)/2
8,2,1,1 14968800 =COMBIN(12,8)*COMBIN(4,2)*FACT(7)
8,1,1,1,1 2494800 =COMBIN(12,8)*FACT(7)
7,5 13685760 =COMBIN(12,7)*FACT(6)*FACT(4)
7,4,1 17107200 =COMBIN(12,7)*5*FACT(6)*FACT(3)
7,3,2 11404800 =COMBIN(12,7)*COMBIN(5,3)*FACT(6)*FACT(2)
7,3,1,1 11404800 =COMBIN(12,7)*COMBIN(5,3)*FACT(6)*FACT(2)
7,2,2,1 8553600 =COMBIN(12,7)*COMBIN(5,2)*COMBIN(3,2)*FACT(6)/2
7,2,1,1,1 5702400 =COMBIN(12,7)*COMBIN(5,2)*FACT(6)
7,1,1,1,1,1 570240 =COMBIN(12,7)*FACT(6)

From the bottom-right cell of the first table, we observe there are 312,888,960 combinations that result in failure. The total ways to arrange those numbers is represented by 12!, equating to 479,001,600. Therefore, the likelihood of failing is 312,888,960 divided by 479,001,600, resulting in a 65.32% failure probability. Hence, the success probability calculates to 100% minus 65.32%, which equals 34.68%.

This inquiry is a topic of discussion in my forum at Wizard of Vegas .

Greetings! I possess a coupon that permits me to push a hand of 22. I can retain this coupon until my first 22 appears. It cannot be used for doubles or splits. What would the value of this coupon be?

MrGoldenSun

In short, the value of the coupon corresponds to the maximum bet permitted. Simply wait for a 22 to occur, play it, and you will walk away from the table with an additional unit.

A more detailed analysis would need to consider the implications of waiting for a 22. While I don’t have exact figures, I can provide an estimation.

The player's cost due to the dealer's push-22 rule is approximately 6.91%. Nevertheless, the dealer will manage to achieve a 22 more frequently since the player’s own busts won't affect the outcome. Based on the rules, players tend to bust around 15.7% of the time. Assuming that this is unrelated to the dealer's bust probability (though it isn’t), the dealer’s bust probability becomes 6.91%/(1.0-0.157), which approximates to 8.2%.

I admit this is a rough calculation, but if we assume the chance of the player obtaining 22 matches the dealer's odds, then each time the player sees the chance of getting a 22 at about 8.2%, it means the player will achieve a 22 on average once every 1/0.082, which totals around 12.2 hands.

Assuming the base game has a house edge of 0.75%, the cost arising from playing 12.2 hands under that edge would be calculated as 12.2 times 0.0075, equaling roughly 0.0915. Subtracting this amount from the one unit value gives the coupon a value of about 1.0 - 0.0915, translating to approximately 91% of its face value.

This inquiry is a topic of discussion in my forum at Wizard of Vegas .