Ask The Wizard #318
What approach should a player take in the Race Game on The Price is Right if they are unfamiliar with the prizes' prices?
To assist those who are new to the game, I’m sharing a video that illustrates how it’s played.
I propose that this particular approach minimizes the average number of attempts needed. While there are alternative strategies that could yield the same results, none exceed this one.
To implement the strategy, you should number the four price tags from 1 to 4. Assign them to the prizes based on your previous success rate, starting with the first tag on the leftmost prize.
Race Game Strategy
| History | Prize 1 | Prize 2 | Prize 3 | Prize 4 |
|---|---|---|---|---|
| None | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
The subsequent table displays the likelihood of needing between 1 and 5 turns out of the 24 different configurations for the four price tags.
Turns Required
| Turns | Number | Probability |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| Total | 24 | 100.00% |
By calculating the dot product, we find that the average number of turns required with this approach is 3.29167.
This topic was raised and is currently discussed on my forum at Wizard of Vegas .
In the episode of Jeopardy aired on September 18, 2019, one of the categories was 'Describe the Casino Game.' A clue given was, 'Dressed and playing to the 9's; Banker’s hours; What brings you to Monaco, Mr. Bond?'

The answer provided was 'baccarat,' which was deemed correct. However, wasn’t Bond playing chemin de fer instead?
Yes, indeed Bond was playing Chemin de fer , not baccarat As a point of clarification, here are the primary distinctions:
- The banking role rotates among the players at the table, and the player acting as the banker automatically has the Banker hand.
- Both the Player and the Banker have the liberty to decide on drawing a third card, provided they don’t already have a natural two-card total of 8 or 9.
Note:
When discussing baccarat or chemin de fer, I capitalize the names of the bets to prevent any misunderstanding regarding the participants in the game.
That brings us to the initial scene featured in the Dr. No video clip below. Here, we observe not only the banking role rotating and the players’ freedom to decide on a third card but also see Bond explicitly refer to the game as 'chemin de fer' at the 2:11 mark in the video.
The following video compilation captures several chemin de fer moments from three different films.
Here are the starting points for each of those scenes:
- 2:09 — Thunderball
- 4:19 — On Her Majesty's Secret Service
- 7:30 — For Your Eyes Only
In all three scenes, we notice players taking on the bank role and exercising their free will concerning the decision to draw a third card, particularly illuminated in For Your Eyes Only, where the odds are analyzed.
Lastly, here is a scene from Goldeneye.
In this scene, we once again observe the role of the banker rotating and the freedom to draw a third card. However, it’s notable that the female character refers to the game as 'baccarat' at the 0:45 mark, which I would categorize as a 'character error.'
To sum up, there’s no doubt that Bond was indeed playing chemin de fer in each of the films. Technically, I believe that the judges erred in accepting 'baccarat' as a valid response. Nonetheless, I don’t hold it against them, as it would be overly ambitious to expect the average contestant to distinguish between baccarat and chemin de fer. Their leniency is evident, especially when they accepted the answer 'The Mooch' instead of Anthony Scaramucci.
This topic was raised and is currently discussed on my forum at Wizard of Vegas .
As asked in the movie Mean Girls , what is:
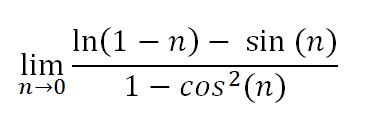
Let’s begin by examining a graph where n is plotted on the x-axis and f(n) on the y-axis.
As observed, the limit approaches infinity on the left side and negative infinity on the right. Because it approaches different values from either side, we conclude that there is no limit.
Nevertheless, let's tackle the question without relying on the graphical representation. L'Hôpital's rule According to the rule, if the limit of f(x)/g(x) leads to the form 0/0, then the limit can be determined using the derivatives of f(x) and g(x). Thus, let’s compute f'(x) and g'(x).
f\"(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g\"(n) = (1 - cos2(n)) d/dn = sin2(n) d/dn
Utilizing the product rule, we will analyze sin.2(n) d/dn
sin2(n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n).
Next, let's solve for f\"(n) and g\"(n) at n = 0.
f\"(0) = -1/(1-0) - cos(0) = -2.
g\"(0) = 2sin(0)cos(0) = 0
Therefore, f'(0)/g'(0) = -2/0 results in negative infinity. Consequently, the limit of the initial function cannot be defined.

I want to applaud the screenwriters of Mean Girls for accurately portraying mathematical concepts in the film. Even films with a serious mathematical focus, like Good Will Hunting, often misrepresent mathematical principles.