Ask The Wizard #313
What is the variance in Cleopatra Keno? ?
Just a reminder for our readers: Cleopatra Keno operates similarly to traditional keno, but with a twist—if the last ball drawn aligns with any of the player's selections and leads to a win, the player earns an additional 12 free plays with a 2x multiplier. Note that these free games do not generate further free games.
Since you didn't mention the number of picks or the payout table, we'll use the example of the 3-10-56-180-1000 pick-8 payout table to illustrate. Let's begin calculating the expected return.
In keno, the different combinations for hitting x balls out of y is determined by selecting x balls from a set of 20 and y-x from a set of 60. In Excel notation, this is written as combin(20,x) multiplied by combin(60,y-x). To remind you, combin(x,y) is calculated as x!/ (y!*(x-y)!), and x! equals 1 multiplied by 2, multiplied by 3, and so forth up to x.
After that explanation, here is the expected return table for this payout structure. The column on the right indicates the expected square of potential winnings, which will be important for our next steps.
Pick 8 Keno
| Event | Pays | Combinations | Probability | Return | Return^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| Total | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
Now, let's work on finding the average bonus amount. From the table above, we can see that the average payout without considering the bonus is 0.593301. With the bonus, players receive 12 doubled free spins, leading to an expected payout from the bonus of 2 times 12 times 0.593301, which equals 14.239212.
Next, we will determine the likelihood of receiving the bonus. If a player successfully identifies four numbers, the chance that the 20th ball drawn corresponds with one of these four is 4 out of 20. Generally, if a player has matched c numbers, the chance that the 20th ball contributed to that win is c/20.
The formula to establish the probability of securing the bonus involves the calculations for catching 4 through 8 numbers: we add prob(catch 4) multiplied by (4/20), prob(catch 5) multiplied by (5/20), and so on through prob(catch 8) multiplied by (8/20). We have previously calculated the likelihood of each winning outcome using the return table. Consequently, we'll sum up these probabilities to find the total for winning the bonus.
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644.
Equipped with the probability of winning the bonus and the average bonus payout, we can evaluate the expected return from the bonus as 0.021644 multiplied by 14.239212, resulting in 0.308198.
While not essential for our calculations, it’s good to note that the total return for the game is the sum of the returns from both the base game and the bonus, yielding 0.593301 plus 0.308198, which equals 0.901498.
Now, let's dive into the concept of variance. As a quick refresher, the general principle concerning variance is as follows:
The relationship is given as var(x + y) = var(x) + var(y) + 2*cov(x,y), where 'var' denotes variance and 'cov' denotes covariance. Specifically, in the context of this game:
Total variance is determined by the variance of the base game added to the variance of the bonus, plus twice the covariance between the base game and the bonus.
The basic formula for calculating variance involves the expression E(x^2) - [E(x)]^2. In simpler terms, this means taking the expected square of the winnings and subtracting the square of the expected winnings.
Now, let’s compute the variance for the base game. Recall when we mentioned earlier that we would need the expected winnings squared from our initial table. The bottom right cell of that table indicates the expected winnings squared at 19.530214. Since we have previously established the expected win at 0.593301, we find the variance for the base game by calculating 19.530214 - 0.593301.2= 19.178208.
Now, let’s evaluate the variance for the bonus provided that it has already been activated. To grasp this fully, just remember:
var(ax) = a2x, where a is a constant.
Additionally, keep in mind that the variance of n random variables x equals nx.
Thus, if x represents the base winning in a bonus round, the overall variance for the bonus now becomes 2 multiplied by 12 multiplied by x. From earlier, we've deduced that the variance for a single spin in the base game, without taking the bonus into account, is 19.178208. Hence, the variance for the bonus segment, assuming the bonus has already been triggered, is 2 times 12 times that variance.2However, we need to consider the variance of the bonus before any balls are drawn, including the chance that the bonus might not be won at all. We cannot simply multiply the bonus variance by the chance of winning it. Instead, recall that var(x) = E(x^2) - [E(x)]^2. Let's rearrange that to express:2× 12 × 19.178208 = 920.554000.
We have already established both the average and variance for the bonus, so the expected square of the winnings from the bonus turns out to be 920.554000 added to 19.178208.
E(x^2) = var(x) + [E(x)]^2
Consequently, before any balls are drawn, the expected square of the winnings from the bonus calculates to prob(bonus) multiplied by E(x^2), equalling 0.021644 multiplied by 1123.309169 to give us 24.313239.2= 1123.309169.
Previously, we evaluated the expected winnings from the bonus before any balls are drawn at 0.308198. Therefore, the overall variance for the bonus before drawing any balls is 24.313239 - 0.308198.
Next, we’ll compute the covariance. You might wonder, \"What is the relationship between the winnings from the base game and the winnings from the bonus?\" The reason is that the last ball drawn must play a role in achieving a win in order to activate the bonus. Given that the last ball did contribute to a winning outcome, the average payout increases. To clarify, Bayes' theorem concerning conditional probability states that:2= 24.218253.
Now, let's revisit our return table for the base game, this time assuming the last ball drawn resulted in a win:
P(A given B) = P(A and B)/P(B).
The bottom right cell indicates that, presuming the last ball drawn was indeed a hit, the average payout is recorded at 6.757734.
Pick 8 Keno given Last Ball Hit
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| Total | 627,414,903 | 1.000000 | 6.757734 |
Also, bear in mind what you learned in your college statistics courses:
For our situation, we define x as the win from the base game and y as the win from the bonus. Let’s focus on calculating exp(xy) first.
cov(x,y) = exp(xy) - exp(x)*exp(y).
Exp(xy) is determined by taking the probability of winning the bonus multiplied by the average win from the base game while the bonus was active multiplied by the average bonus win during that same circumstance. Since it’s evident that average(bonus win given no bonus) is 0, we can simplify our equation to:
Exp(xy) becomes the probability of the bonus win multiplied by the average win from the base game while the bonus was being played, expressed as:
Having already derived E(x) and E(y), our covariance is then:
0.021644 × 6.757734 × 14.239212 = 2.082719.Revisiting the overarching equation for variance when we include covariance, we arrive at:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865.
The total variance is calculated as var(base game) plus var(bonus) plus 2 multiplied by cov(base game and bonus), resulting in 19.178208 plus 24.218253 plus 2 times 1.899865, which comes to 47.196191. Thus, the standard deviation, derived from the square root of this total variance, is 6.869948.
And there you have it. This took several hours, so I trust you'll find it valuable. This topic has been addressed and further deliberated in my forum at
It has come to my attention that the probability of marriages ending in divorce—often quoted as 50% in the United States—is typically calculated by comparing the number of divorces to the number of marriages within the same timeframe. Is this method accurate? Do you believe it fairly represents the statistic? I question its validity since it evaluates divorces over a short range compared to marriages occurring over a longer duration.
If the population and its age demographics remained unchanged, a divorce probability of 50% would imply an anticipated ratio of one divorce for every two marriages in any selected period, provided a substantial sample size. Wizard of Vegas .
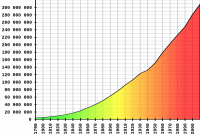
However, given the fluctuating population, the accompanying graph indicates a growth rate of 10.71% per decade for the U.S. population, which translates to approximately 1.02% annually. Let’s simplify and assume it's a steady 1%.
Also, statistics reveal that the typical duration of a failing marriage is about 8 years.
If currently observing a ratio of 1 divorce for every 2 marriages, what would be the average likelihood that a particular marriage culminates in divorce?
Map source: U.S. Census
According to fatherly.com The divorces being registered at present stem from marriages that occurred 8 years prior, during which the population comprised around 92.35% of its current size. Hence, simple arithmetic indicates that the actual divorce likelihood may be approximately 54.14%.
To start, as per CDC data, the marriage rate is about 6.9 per 1000 population each year. Although this number might not directly relate to the original question, it offers a clearer picture of the figures at play.
If we assume the population 8 years ago was around 300 million, that yields 0.69% * 300 million = 2,070,000 marriages in that particular year.
Let's check that.
If approximately 54.14% of those marriages end in divorce eight years later, we would expect to see 1,120,698 divorces reflected today.
Calculating the ratio gives us 1,120,698 divided by 2,070,000, resulting in an observed divorce rate of 50% at present.
Just to clarify, yes, I acknowledge not every divorce unfolds precisely after eight years. However, I maintain that the overall figure is unlikely to deviate significantly from my derived estimate of a 54.14% divorce probability.
This question is raised and discussed in my forum at
In your workplace, if 100 employees engage in a Secret Santa gift exchange, each person writes their name on separate pieces of paper, puts them into a hat, and then everyone randomly draws a name to determine whom they will give a gift to.
The inquiry here concerns the average number of closed loops that will occur. A closed loop is illustrated when, for instance, Gordon gives a gift to Don, Don gifts Jon, Jon gifts Nathan, and Nathan gifts back to Gordon. Another instance of a closed loop could be drawing one’s own name. Wizard of Vegas .
Let’s examine the selection process, where each person picks a name sequentially. With each draw, there are two possible scenarios:
Either the name of the person drawing has already been selected by someone else, or their name is still available for picking.
For any individual drawing a name, let’s assume there are n individuals remaining in the drawing pool.
- If the name drawn belongs to someone who has already been chosen, there's a 1/n chance that this picker will select a name that creates a closed loop involving their own name. For instance, if Amy is currently drawing and her name is already chosen by Bob while Bob's name is with Charlie, who is still in the pool, then Amy has a 1/n chance of drawing Charlie's name, thereby completing the loop.
- Conversely, if the name being picked has yet to be selected, there exists a 1/n chance that the individual might draw their own name, which would also complete a loop.
Regardless of whether a loop is formed, if the picker doesn’t create one, they still join a larger chain, and that chain will eventually be completed by another participant. Each unique chain should only be accounted for once it's closed.
As a rough estimate for a sufficiently large number of participants, n, is expressed as ln(n).
This inquiry is addressed and discussed in my forum at
On the value of an additional guaranteed wild in a video slot machine, this can vary broadly based on several factors. My interpretation of your question is focused on the worth of an extra wild beyond what the player might typically encounter. The impact of that added wild fluctuates significantly depending on the number of rows displayed on the screen. For instance, with three rows, the additional wild will positively influence 1/3 of the potential paylines. In contrast, for four rows, the impact would be less, affecting just 1/4 of the paylines.
Thus the answer is 1/100 + 1/99 + 1/98 + ... + 1/1 = 5.187377518.
To respond to your inquiry, I analyzed the game in question, and I have constructed a table that illustrates the increase in expected value resulting from an extra wild when contrasted to a scenario where the number of wilds is random.
Strategic and accurate mathematical approaches for casino games like blackjack, craps, roulette, and an array of others are available to explore. Wizard of Vegas .
Please check your email for a link we provided to finalize your registration.
Explore the Top Online Casinos Available in Your Region
Tool for Calculating Lottery Jackpot Ticket Sales Cleopatra Engage in Slot Competitions with Grand Prize Pools
Value of Extra Wild in Cleopatra
| Reel | 3 Rows | 4 Rows |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |