Ask The Wizard #284
Have you caught wind of the car dealership in Seattle that ended up paying $420,000 due to the Seahawks' shutout against the Giants? I read that they had to take out a $7,000 insurance policy for that outcome. What do you think would be a reasonable premium?
According to the article A Washington car dealership is shelling out $420,000 after the Seahawks shut out the Giants. The dealership had an intriguing promotion where they pledged to pay twelve lucky winners a hefty $35,000 each if the Seahawks managed to shut out the Giants in their week 15 clash on December 15, 2013. They even mentioned they paid $7,000 for an insurance policy to cover such a possibility.
Examining the NFL games from the 1983 to 2012 seasons, there were instances where one side was completely shut out. However, considering that the Giants were seven-point underdogs in a game with an average total score, I argue that the chances of them being shut out were higher than the norm. The game's total was set at 41 points. Let's do a bit of algebra to figure out the estimated points the Giants might have scored.
Let:
s=Seahawks points
g=Giants points
From what we know, s + g = 41 and s = g + 7, derived from the point spread and the over/under.
Let’s substitute the second equation back into the first:
(g+7) + g = 41
2g +7 = 41
2g = 34
g = 17
Now, we'll analyze the shutout probability based on each team's estimated point total from the 1983 to 2012 seasons. I skipped over any cases where the sample size was zero.
Probability of Shutout
| Estimated Points |
Sample Size | Shutouts | Ratio |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11.00 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12.00 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16.00 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18.00 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21.00 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
The following steps are quite comprehensive, but I've devised a formula that calculates the probability of a shutout based on estimated points.
p = Estimated points.
x = 1.562545 -0.302485 * p
probability of shutout = ex/(1+ex)
The chart below illustrates the actual versus estimated probability of a shutout for point totals ranging from 14 to 22.
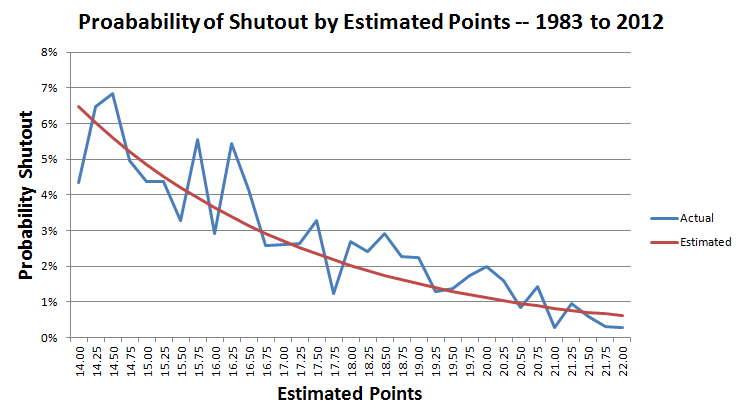
In the specific game we're discussing, the Giants were expected to score around 17 points.
Using the formula above the table:
x = 1.562545 -0.302485 * 17 = -3.579706
The probability of a shutout has been calculated as exp(-3.579706)/(exp(-3.579706)+1), which equals 2.71%, precisely 0.0271275.
Considering the dealership's potential $420,000 payout in the event of a Giants shutout, the fair cost of the insurance policy should have been $420,000 multiplied by 0.0271275, totaling $11,394. Insurance providers usually charge double the fair price for unique promotions like this, implying I would expect a premium around $22,788. Therefore, the $7,000 premium the dealership paid was quite a bargain. If the manager scrutinizes the calculations, I wouldn't want to be in the position of the person who figured out that $7,000 premium.
This topic was examined and discussed in my forum at Wizard of Vegas .
What evidence exists to assert that there's no largest prime number?
Let's indulge in a hypothetical scenario where there's a largest prime number. We can label the primes as p1=2, p2=3, p3=5, p4=7, and so forth up to pL, which is purportedly the largest prime.
Now let's define the number x = p1*p2*p3*p4*..*pL + 1.
Being prime implies that no smaller prime can divide it without leaving a remainder.
If we divide x by p1, p2, p3, ..., or pL, we consistently get a remainder of 1.
You might suggest that perhaps a prime larger than pL can divide x evenly. That may be true, but in doing so, you would have uncovered a prime larger than the claimed largest prime. Alternatively, if that’s not the case, then x itself becomes a new largest prime, hence proving the original assumption of having a largest prime number wrong through contradiction.
This question was raised and explored in my forum at Wizard of Vegas .
Do you agree with the article titled Mathematical reasoning suggests you should purchase a Mega Millions ticket immediately. at Business Insider?
I must disagree with that stance. It’s a poorly researched piece, and Business Insider should reconsider its publication.
First, the article came out on December 17, 2013, just before the drawing for the $636 million jackpot that evening. Let's delve into the math to better understand the worth of a $1 ticket. The table below illustrates the probabilities and expected returns for all potential outcomes associated with the $636 million jackpot, without yet accounting for aspects like lump sum deductions, taxes, and sharing the jackpot.
Mega Millions -- $636 Million Jackpot
| Catch | Mega Ball | Pays | Combinations | Probability | Return |
|---|---|---|---|---|---|
| 5 | Yes | $636,000,000 | 1 | 3.86E-09 | 2.456634 |
| 5 | No | $1,000,000 | 14 | 5.41E-08 | 0.054077 |
| 4 | Yes | $5,000 | 350 | 1.35E-06 | 0.006760 |
| 4 | No | $500 | 4,900 | 0.000019 | 0.009463 |
| 3 | Yes | $50 | 24,150 | 0.000093 | 0.004664 |
| 3 | No | $5 | 338,100 | 0.001306 | 0.006530 |
| 2 | Yes | $5 | 547,400 | 0.002114 | 0.010572 |
| 1 | Yes | $2 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | Yes | $1 | 12,103,014 | 0.046749 | 0.046749 |
| Loser | $0 | 241,288,446 | 0.932008 | 0.000000 | |
| Total | 258,890,850 | 1.000000 | 2.630865 | ||
The calculations show that a $1 ticket will yield an expected return of $2.630864. After subtracting the initial dollar spent on the ticket, the anticipated profit is $1.630864. Business Insider reported $1.632029, which only varies by 0.001164, so it's negligible.
However, there are three significant factors that considerably reduce the ticket's value:
- The lump sum penalty.
- Taxes.
- Jackpot sharing.
Let's look at them one at a time.
Typically, large lottery jackpots, such as Mega Millions, are paid out in the form of an annuity spread over about 30 years. If a winner wants to claim a lump sum—something most people prefer—they face a substantial reduction. This is reasonable because a dollar today holds more value than a dollar in the future. For the December 17, 2013 drawing, the total prize amount dropped to $347.6 million, or approximately 54.65% of what was advertised.
Next, we need to factor in taxes. The highest federal income tax rate is 39.6%. State taxes can fluctuate from 0% to 12.3%, so let’s assume an average tax rate of around 6%. After accounting for 45.6% in taxes, that leaves $189.1 million.
The next element to consider is the sharing of the jackpot. Notably, after the drawing on October 22, 2013, Mega Millions altered its rules to a format known as 75-15, wherein five numbers are drawn from a selection of 1 to 75, and one from a separate pool of 1 to 15. This adjustment decreased the odds of winning to 1 in 258,890,850, possibly aiming for larger jackpots. Analyzing the 17 drawings since the rule change, using data on jackpots and sales from LottoReport.com , reveals a clear exponential correlation between the size of the jackpot and the demand for tickets. I found a similar pattern with the Powerball lottery. By employing exponential regression, I calculated the total tickets sold (in millions) using the formula 12.422 × exp(0.0052 × j), where j denotes the jackpot size (in millions). For instance, with a jackpot of $636 million, expected sales would be 12.422 * exp(0.0052*636) = 339.2 million. Actual sales were recorded at $337 million, making the estimations very close.
Based on the actual ticket sales of 336,545,306, we could anticipate about 336,545,306/258,890,850 = 1.300 winners. A pertinent consideration is how many other individuals you would expect to share your winnings with if you win. This query can be addressed through the Poisson distribution. With an average of 1.3 winners, the chance of having exactly x winners is calculated as exp(1.3) × 1.3 / fact(x). The upcoming table provides probabilities for having 0 to 10 additional winners, illustrating your portion of the jackpot in each scenario, along with the expected value, presuming you secure a win.xExpected Jackpot Share Assuming an Average of 1.3 Additional Winners
The bottom-right cell illustrates that you can anticipate retaining 55.96% of the winnings, while the remaining 44.04% would go to the other winners you'll have to divide the jackpot with.
| Other winners | Probability | Jackpot share | Expected share |
|---|---|---|---|
| 10 | 0.000001 | 0.090909 | 0.000000 |
| 9 | 0.000008 | 0.100000 | 0.000001 |
| 8 | 0.000055 | 0.111111 | 0.000006 |
| 7 | 0.000339 | 0.125000 | 0.000042 |
| 6 | 0.001827 | 0.142857 | 0.000261 |
| 5 | 0.008431 | 0.166667 | 0.001405 |
| 4 | 0.032429 | 0.200000 | 0.006486 |
| 3 | 0.099786 | 0.250000 | 0.024946 |
| 2 | 0.230283 | 0.333333 | 0.076761 |
| 1 | 0.354295 | 0.500000 | 0.177148 |
| 0 | 0.272545 | 1.000000 | 0.272545 |
| Total | 1.000000 | 0.559602 |
Now, the once-promised $636 million jackpot is now effectively down to $189.1 million multiplied by 55.96%, equating to $105.8 million. Let's examine what the return table indicates with this new jackpot figure.
According to the revised calculations, the expected return stands at 58.29%. This means that your $1 investment is likely to generate around 58 cents in return, leading to an anticipated loss, or house edge, of about 42%. Does this align with the suggestion to purchase a ticket?
Mega Millions -- $105.8 Million Jackpot
| Catch | Mega Ball | Pays | Combinations | Probability | Return |
|---|---|---|---|---|---|
| 5 | Yes | $105,800,000 | 1 | 3.86E-09 | 0.408666 |
| 5 | No | $1,000,000 | 14 | 5.41E-08 | 0.054077 |
| 4 | Yes | $5,000 | 350 | 1.35E-06 | 0.006760 |
| 4 | No | $500 | 4,900 | 0.000019 | 0.009463 |
| 3 | Yes | $50 | 24,150 | 0.000093 | 0.004664 |
| 3 | No | $5 | 338,100 | 0.001306 | 0.006530 |
| 2 | Yes | $5 | 547,400 | 0.002114 | 0.010572 |
| 1 | Yes | $2 | 4,584,475 | 0.017708 | 0.035416 |
| 0 | Yes | $1 | 12,103,014 | 0.046749 | 0.046749 |
| Loser | $0 | 241,288,446 | 0.932008 | 0.000000 | |
| Total | 258,890,850 | 1.000000 | 0.582898 | ||
The article claims that, provided fewer than 730 million tickets are sold—which seems plausible—then the expected value of a ticket would still be positive, suggesting you should think about buying a Mega Millions ticket today.
The sold tickets were well below the 730 million threshold, making it an extremely poor investment. Nevertheless, the article responsibly notes:
\"It’s essential to keep in mind that there are many caveats to this analysis. Taxes might severely impact your expected winnings; the federal government could claim around 40%, while your home state may take anywhere from 0% to 13%.\"
Many people have been purchasing tickets, and as discussed, this significantly increases the likelihood of sharing the jackpot with other winners, subsequently lowering your payout.\" - Business Insider
These are substantial caveats! They shouldn't merely be mentioned in passing at the conclusion; rather, they should be integrated into the analysis from the outset.
Though you didn't specifically ask, my computations indicate that investing in Mega Millions is unwise. Based on the exponential ticket demand concerning jackpot size, I've deduced that the optimal jackpot amount to play is around $545 million. Beyond this amount, you'll likely end up sharing with too many other winners, and at that jackpot size, a player can expect a return of 60.2% or a loss of 39.8%. That would be the best scenario possible.
In summary, I stand firm in my disagreement with Business Insider for misleading readers with flashy headlines and neglecting to perform a thorough analysis of taxes and potential jackpot sharing.
This query is explored and discussed in my forum at
Strategies and accurate information regarding casino games like blackjack, craps, roulette, and many others. Wizard of Vegas .


