Ask The Wizard #265

It appears you might be mixing up mean and median values. For instance, let’s apply my scenario. As a male aged 45, my expected lifespan is approximately 78.11 years, yet I have over a 50% likelihood of surviving until I turn 80.

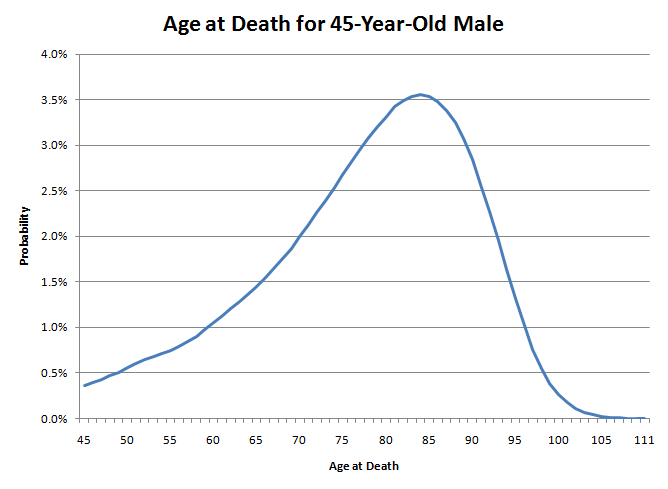
Thinking about my lifespan is similar to aiming at a board with darts. Observing the graph, you can see that the left side has a much broader area compared to the right. This indicates my current death probability is relatively low. Nevertheless, as I age, the chances of dying in the subsequent year increase. To illustrate, for a 45-year-old male, the odds of living to 46 are impressively high at 99.64%. In contrast, once a man turns 85, the chance of living to 86 drops to just 89.21%. It's akin to nature gradually intensifying pressure on you; initially, it may not be fatal, but as the years go by, the risk escalates. Particularly, once you hit late seventies, nature seems to hasten the inevitability.

If a group of 45-year-old men were to throw darts at this graph, about 49.96% would land in the age range of 45 to 79, and 50.04% would find themselves between 80 and 111. Those fortunate to hit the right section of the graph are unlikely to surpass age 80 by much, as a male who reaches that age can generally anticipate merely 7.78 additional years. Conversely, many in the unfortunate half who don’t make it to 80 will pass away significantly earlier. This is why early deaths can lower the average life expectancy.

Consider a similar scenario involving a die with the numbers 10, 20, 30, 31, 32, and 33. While the average value calculated is 26, the odds show a 66% chance of rolling above that average.

To illustrate the differences between mean and median, think about what happens if we add two more deaths to our data set—one at age 46 and another at age 81. While the probability of reaching 80 remains unchanged, the average life expectancy for someone who is 45 would decrease.

This topic was brought up and deliberated in the online discussion forums of my affiliated site. Wizard of Vegas .

That’s an insightful inquiry. According to the house rules, players are advised to split their five aces while using two of them for the lower hand. However, the exception is that if players can play two kings for the lower hand, they should keep the five of a kind for the higher hand. pai gow poker page Research indicates there are seven house rules derived from Las Vegas and Atlantic City, and all incorporate this exception. Meanwhile, the three rules established in other locations do not include it.

The odds of drawing four aces, one joker, and two kings come to approximately 1 in 25,690,513. Assuming the dealer is banking, the only time this specific rule would be useful is when the player already holds four of a kind or better in their higher hand, which generally happens around 1 in 300 times. Therefore, the likelihood of both events occurring simultaneously is approximately 1 in 7.6 billion.

Data from the Nevada Gaming Control Board noted there were 306 pai gow poker tables operational in Nevada as of 2009. If we optimistically estimate gameplay at 60 hands per hour with two players per table around the clock, it would take roughly 23.7 years for this rule to actually influence a game's result.

Thus, casinos demand that every pai gow poker dealer memorize this specific exception, despite the likelihood that it has yet to affect any game outcomes throughout history. I suspect that the individual who initiated this rule was also the one who determined that the A2345 straight, commonly called 'the wheel', ranks as the second highest straight in the game.

This question touches on a classic probabilistic issue. Many mistakenly believe the answer is 18, based on the probability of rolling a 12 being 1 in 36, leading them to 18 * (1/36) = 50%. However, following this reasoning, the chance of rolling a 12 in 36 attempts would inaccurately be considered certain, which is not the case. For the correct approach, let r denote the number of rolls. The chance that a given roll doesn’t yield a 12 is 35/36. Hence, the probability of rolling zero 12s in r rolls would be (35/36) raised to r.^rConsequently, there isn't a straightforward answer. After calculating, the probability of rolling a 12 in 24 rolls stands at 1 - (35/36)' = 49.14%, while in 25 rolls, it is 1 - (35/36).

(35/36)^r= 0.5
log(35/36)^r= log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051

If you're looking to place a bet regarding this, you could argue that you will successfully roll a 12 in 25 attempts whereas another individual would fail to achieve that in 24 rolls. In either instance, you'd likely hold a favorable position at even odds.²⁴I noticed a sports book in Las Vegas posted a profoundly inaccurate total for a college football game. The actual market figure was 43, but they offered it at 53. I decided to place small under bets around 20 times, to avoid capturing attention or influencing the line. Predictably, I came out ahead. Now, I'm apprehensive about cashing in on these bets. Is it reasonable for the casinos to deny payment?²⁵= 50.55%.

My bet would be 10 to 1 that you will be compensated, although they might potentially have a few remarks for you first. My hesitation arises from the fact that a sports book can reverse a bet made in error, provided the approval of the Gaming Control Board is secured.

Even though this privilege exists, anecdotal evidence suggests it is rarely enforced. Please keep me updated on the outcome.

P.S. I later received word from the individual who posed the question that they were paid without significant hassle.

Visualize an infinitely stretchable rubber band measuring 1 kilometer in length when not stretched. It expands at a speed of 1 kilometer per second. Now, imagine an ant positioned at one end of this rubber band. The moment the band begins to stretch, the ant moves toward the opposite end at a speed of 1 centimeter per second relative to how far along it is. Will this ant ever reach the end of the rubber band? If so, when might that occur?

Here are mathematically validated strategies and insights for various casino games, including but not limited to blackjack, craps, and roulette, along with hundreds of others.

Yes, it will, after e^100,000-1 seconds. See my mathproblems.info site, problem 206, for two solutions.

This topic was brought up and deliberated in the online discussion forums of my affiliated site. Wizard of Vegas .