Ask The Wizard #261

To address this inquiry, I plotted the average points scored per week in the NFL from 1983 to 2009. Below is the chart illustrating these findings.

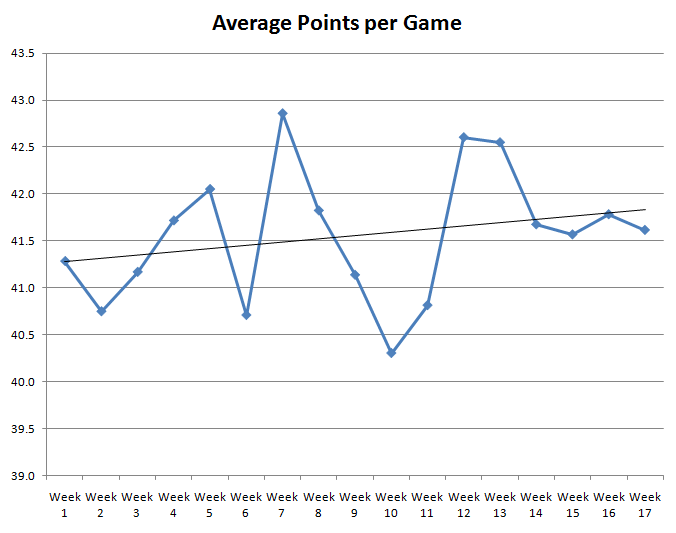
From the graph, it's evident that the scores fluctuate significantly over time. The narrow black line represents a least-squares regression line, indicating a slight upward trend overall. This suggests that as the season advances and temperatures drop, the average points scored tend to increase a bit, although this might just reflect random fluctuations.

I've reached the limit of my analysis on this topic. To gain a broader understanding of how weather impacts sports betting, I consulted my friend Jason Been, an authority in this field. Here’s his perspective:

Generally, wind emerges as the major weather variable that influences the outcome of a game; however, it's not the sole factor. In sports like baseball, outdoor conditions such as shadows can significantly impact performance, particularly during afternoon games in early or late seasons. Contrary to popular belief, rain or snow has a minimal effect on football since it typically slows both offenses and defenses in equal measure. For instance, in the matchup between a wide receiver and a defensive back, the rain impacts their speed similarly, providing no advantage to either side. Yet, strong winds can drastically hinder a passing game in football, as well as kicking. I've witnessed instances where teams reliant on passing had to shift to running plays consistently due to fierce crosswinds. Although it doesn't occur frequently, wind can decisively determine the outcome of a game.

This topic was brought up and thoroughly debated in the forum associated with my sister site. Wizard of Vegas .

I inquired about this with an experienced game manager from a Las Vegas table. He explained that any portion of the odds bet exceeding the permitted multiple of the line bet would be settled at the odds designated for place bets. This discussion circulated in the forum of my affiliate site. Wizard of Vegas .

Analyzing data from the NFL seasons spanning from 2000 to 2009 reveals that this probability is approximately 57%.

This riddle is featured in a BBC show. Quite Interesting For the answer and detailed solution, scroll down 100 lines.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

I've calculated the probabilities of A winning based on each initial target. Notably, A's best chance of survival is achieved by intentionally shooting into the air.

Truel Odds

Strategy	Prob. Win
Air	13.887%
A	0.000%
B	12.560%
C	13.094%

To arrive at the solution, we define Pr(X) as the probability that only group X remains after a round. The term Pr(X*) denotes the likelihood of group X ultimately winning the round, continuing until a hit occurs. We also define Pr(X**) as the probability that player X is the last one standing. To determine the final probabilities, we first analyze scenarios involving two players.

A vs. B

• Pr(A) = 0.1
  
• Pr(B) = 0.9 × 0.6 = 0.54
  
• Pr(AB) = 0.9 × 0.4 = 0.36

If only two players are left, it becomes clear that each will target the other.

• Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
  
• Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375

A vs. C

• Pr(A) = 0.1
  
• Pr(C) = 0.9 × 0.9 = 0.81
  
• Pr(AC) = 0.9 × 0.1 = 0.09

If only two players are left, it becomes clear that each will target the other.

• Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
  
• Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989

B vs. C

• Pr(B) = 0.6
  
• Pr(C) = 0.4 × 0.9 = 0.36
  
• Pr(BC) = 0.4 × 0.1 = 0.04

If only two players are left, it becomes clear that each will target the other.

• Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/0.96 = 0.625
  
• Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/0.96= 0.375

Assuming both survive, they'll continue shooting until only one remains. Thus, we derive the probabilities of each player being the final survivor:

Three Player — A Aims at B

Now we are prepared to investigate the circumstances involving three players. Let’s assume A targets B.

• Pr(A) = 0.
• Pr(B) = 0.
• If A successfully shoots B, C will undoubtedly survive and might or might not hit A in return. The potential outcomes from hitting B are pairs AC and C. Conversely, if A fails to hit B, then B recognizes the greater risk posed by C. If B successfully hits C, both A and B remain. Should B miss, C will aim at the more significant threat, B. If C misses B, all three will continue to survive. However, if C connects with B, A and C will remain. Consequently, the possible outcomes are C, AB, AC, and ABC.
• Pr(C) = 0.1 × 0.9 = 0.09. This scenario occurs if A hits B, followed by C hitting A.
• Pr(AB) = 0.9 × 0.6 = 0.54. This occurs when A misses B, and subsequently, B hits C.
• Pr(BC) = 0.
• Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334. This can happen in two ways: A hits B and C misses A, or A misses B while B misses C, leading to C hitting B.

Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This outcome arises when all three miss their shots.

• Pr(C*) = 0.09/0.964 = 0.093361.
  
• Pr(AB*) = 0.54/0.964 = 0.560166.
  
• Pr(AC*) = 0.334/0.964 = 0.346473.

Using similar reasoning as in the two-player scenarios, we can normalize each outcome based on (1-Pr(ABC))=0.964 to derive the probabilities for each state, given that the game state changes after the round.

• From our previous assessments, we know that if it comes down to A and B, A’s chances of winning are 0.15625, while B’s chances are 0.84375. If A faces C, his odds of winning drop to 0.109890, with C's rising to 0.890110.
• Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A can achieve victory in two scenarios: (1) reaching the AB outcome and winning, or (2) reaching the AC outcome and prevailing.
• Pr(B**) = 0.560166 × 0.84375 = 0.472640. B can claim victory if they reach the AB outcome and emerge as the winner.

Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. C's path to victory involves A eliminating B, and then C taking out A in the initial round, or transitioning to the AC situation where C then wins.

Three Player — A Aims at C

Thus, if A's strategy is to shoot at B first, the likelihood of him being the last one standing is 12.56%.

• Pr(A) = 0.
• Pr(B) = 0.1 × 0.6 = 0.06.
• Pr(C) = 0.
• If A decides to target C and hits, B is guaranteed to survive and might or might not hit A. This presents two potential outcomes: AB and B. If A misses C, B will focus on the more significant threat, C. Should B manage to hit C, both A and B stay in the game. Conversely, if B fails, C will direct their shot at B. If C misses, all three competitors will continue; however, if C hits B, then A and C will remain. Hence, the potential outcomes include B, AB, AC, and ABC.
• Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04 + 0.54 = 0.58. This can occur in two scenarios: first, if A hits C and B misses A; second, if A misses B and B hits C.
• Pr(BC) = 0.
• Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. This can happen when A and B both miss C, permitting C to hit B.

Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This outcome arises when all three miss their shots.

• Pr(B*) = 0.06/0.964 = 0.062241.
  
• Pr(AB*) = 0.58/0.964 = 0.601660.
  
• Pr(AC*) = 0.324/0.964 = 0.336100.

Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This arises when all three miss their shots.

• Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943.
• Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891.
• Pr(C**) = 0.336100 × 0.890110 = 0.299166.

Applying the same reasoning used in the case where A aims at B:

Therefore, if A's strategy is to initially target C, his chances of being the sole survivor increase to 13.09%.

Three Player — A Deliberately Misses

• Pr(A) = 0.
• Pr(B) = 0.
• Pr(C) = 0.
• Pr(AB) = 0.6. This is achieved by B hitting C.
• When A purposefully opts to miss, B will then focus on the greater threat, C. If B successfully hits C, both A and B will continue. Should B miss, C will aim at B. If C misses, all three will survive, but if C manages to hit B, A and C will remain in the game. Hence, the conceivable outcomes are AB, AC, and ABC.
• Pr(BC) = 0.
• Pr(AC) = 0.4 × 0.9 = 0.36. This scenario happens when B misses C, and C successfully hits B.

Pr(ABC) = 0.4 × 0.1 = 0.04. This can happen when all three miss their shots.

• Pr(AB*) = 0.6/0.96 = 0.625.
  
• Pr(AC*) = 0.36/0.96 = 0.375.

Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This arises when all three miss their shots.

• Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865.
• Pr(B**) = 0.625 × 0.84375 = 0.527344.
• Pr(C**) = 0.375 × 0.890110 = 0.333791.

Utilizing similar logic as for the two-player scenarios, we can normalize each outcome using (1-Pr(ABC))=0.96 to derive the probabilities for each state, assuming the game state changes after the round.

This topic was brought up and thoroughly debated in the forum associated with my sister site. Wizard of Vegas .