Ask The Wizard #259
In some Dutch casinos, there's a rule allowing triple imprisonment in roulette. What would the house advantage be for even money wagers under this particular rule? I'm more interested in the detailed breakdown of the calculation rather than just the final answer.
To clarify for those who might be reading this, in many European casinos, if you place an even money bet on roulette and it lands on zero, that bet gets imprisoned. Should the following spin result in a win for that bet, you will receive your original stake back, but no winnings. If the next spin doesn't favor your bet, your wager is lost.
What occurs to bets that are single-imprisoned if the ball lands on zero? In establishments that only allow for a single imprisonment, the bet would be lost. However, certain casinos permit double imprisonment—here, if a double-imprisoned bet wins, it reverts to being a single-imprisoned bet. If a casino has a rule limiting imprisonment to double, encountering another zero would result in a loss for the double-imprisoned bet. By extension, if a casino accepts triple imprisonment, then a bet once double imprisoned would transition to triple imprisonment upon hitting another zero.
The house edge for scenarios where triple imprisonment is allowed calculates to 1.370120%. Before diving into how I reached this figure, let’s first examine the concepts of single and double imprisonment. Imagine beginning with a wager on red.
Let Z = probability of a zero = 1/37.
Let R = probability of a red number = 18/37.
Single imprisonment
pr(push) = ZR = 0.0131482834.
pr(win) = R = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5003652301.
Expected value = pr(win)-pr(loss) = -0.0138787436.
Double imprisonment
In the case where the initial spin results in a zero, the player doesn't lose but instead may continue to push. This means they can repeat the zero result an unlimited number of times before finally landing on red. To put it differently, the ways to achieve a push are as follows:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ..
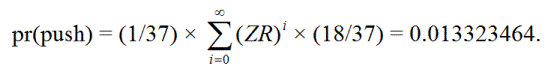
pr(push) = 0.013323464
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001900494.
Expected value = pr(win)-pr(loss) = -0.0137035629.
Triple imprisonment
First, let’s find the probability p1Essentially, a single-imprisoned bet can experience a transition to triple imprisonment by facing another two zeros, eventually returning to its original single-imprisoned state. This sequence can unfold as follows:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ..
Put simply, the bet can oscillate between triple and double imprisonment countless times.
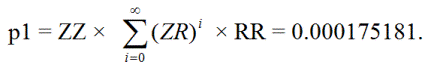
Second, let p2= This is the likelihood that a single-imprisoned wager reaches the first or second imprisonment level and subsequently returns to being single imprisoned.
let p2= ZR + p1= 0.013323464.
The player has the ability to loop back from zero to the first imprisonment level infinitely. Thus, the probability of achieving a push is as follows:
ZR + Z p2R + Z p2 p2R + Z p2 p2 p2R + .. =
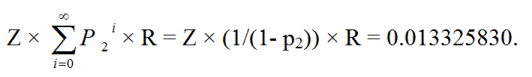
Z × (1/(1- p2)) × R = 0.013325830.
pr(push) = 0.013325830.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876839.
Expected value = pr(win)-pr(loss) = -0.0137011974.
Infinite imprisonment
Although you didn’t inquire, Maff, I've heard that in Spain, they allow for infinite imprisonment. Let's denote p as the probability of a push, which also describes the likelihood of commencing from a certain level of imprisonment, dropping deeper into subsequent levels, and then eventually ascending back to that starting point.
p = ZR + ZpR + ZppR + ZpppR + ..
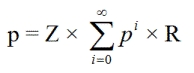
p2- p + ZR = 0
By the Quadratic Formula p = (1-(1-4*RZ)1/2)/2 = 0.0133258620.
pr(push) = 0.0133258620.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876515.
Expected value = pr(win)-pr(loss) = -0.0137011650.
Zeros ignored imprisonment
Lastly, in some casinos, zeros are ignored after the first zero that causes imprisonment. In such cases, the probability of reaching a push is simply calculated as (1/37)×(1/2) = 0.0135135135.
The table below outlines the four distinct types of rules we are discussing.
Imprisonment Odds
| Imprisonment | Win | Push | Loss | Expected Value |
| Single | 0.48648649 | 0.01314828 | 0.50036523 | -0.01387874 |
| Double | 0.48648649 | 0.01332346 | 0.50019005 | -0.01370356 |
| Triple | 0.48648649 | 0.01332583 | 0.50018768 | -0.01370120 |
| Infinite | 0.48648649 | 0.01332586 | 0.50018765 | -0.01370117 |
| Zeros ignored | 0.48648649 | 0.01351351 | 0.50000000 | -0.01351351 |
A heartfelt thank you to ChesterDog and weaselman for their assistance with the math involved. Additionally, my gratitude extends to professor G. Artico and polarprof.it for their contribution to the HTML representation of the summation formula provided above.
This inquiry was brought up and deliberated within the discussion forum on my affiliated site. Wizard of Vegas .
Let’s consider an assumption regarding a specific model of video poker.
- 6-5 Bonus Poker progressive.
- 2% meter rise on royal flush.
- 5-coin game.
Now assume the following about me.
- Minimum return to play of 100.5%.
- I am capable of playing a progressive machine until I hit the jackpot.
- I have mastered the optimal 6-5 Bonus Poker strategy tailored for a royal flush paying 4000 coins.
What’s the minimum jackpot I should aim for to justify my play?
7,281.8 coins is the answer. Interestingly, if one were to play exactly at this jackpot level just once, the expected return would only be 98.5%. However, the reason to play at this threshold is the understanding that you can continue to play until you hit the jackpot. It's akin to receiving a 2% cash back bonus from a slot club program—98.5% return plus a 2% cash back equals 100.5% overall.
It’s worth mentioning that if you begin employing a 4000-coin jackpot strategic approach right at the 7,281.8 jackpot mark, you could expect to gain approximately 201.18 bets. However, should you invest time to learn the strategy adjustments relevant to a 7,281.8 coin jackpot, your projected profit could increase to around 234.31 coins.
On a related note, I recently finished reading a book entitled The Secret World of Video Poker Progressives, authored by Frank Kneeland. This book contains numerous formulas dealing with much more complex progressive scenarios and offers practical advice along with narratives based on his extensive experience leading a team of progressive hunters. I would certainly recommend it to those engaged in advantage play for progressive video poker.
In an Oklahoma casino, there’s a particular case of adding three jokers into a six-deck blackjack shoe. How does this change the odds involved?
Stanford Wong addresses the topic of jokers in blackjack in his work, where he notes that each joker per deck provides an advantage of 4.2% to the player. Therefore, having half a joker per deck equates to 2.1% benefit. His book also offers strategic recommendations on how to declare the value of the joker based on your own cards and the dealer’s up card. Basic Blackjack Are there any studies or statistics available that can shed light on how many blackjack tables in Las Vegas offer a 6-5 payout or any variations considered 'carnival' type?
This inquiry was brought up and deliberated within the discussion forum on my affiliated site. Wizard of Vegas .
According to available data, Las Vegas featured 2099 blackjack tables. The table below outlines the distribution across the four major variations.
According to the September 2010 Current Blackjack Newsletter Accurate strategies and valuable information for casino games such as blackjack, craps, roulette, and many more are documented and available for eager players.
Blackjack Variants in Las Vegas
| Game | Tables | Percent |
| 6 to 5 | 467 | 22.2% |
| Blackjack Switch | 42 | 2.0% |
| Super Fun 21 | 41 | 2.0% |
| Spanish 21 | 6 | 0.3% |
| Total | 556 | 26.5% |
This inquiry was brought up and deliberated within the discussion forum on my affiliated site. Wizard of Vegas .


