Ask The Wizard #253

That's a valid inquiry. To enlighten other readers, let me provide the odds of facing a random hand with each of those two starter hands in a two-player scenario:

K-J Suited vs. A-7 Off-Suit

Hand	Win	Lose	Draw	Expected Value
KJ	0.6148	0.3634	0.0218	0.2513
A7	0.5717	0.3949	0.0334	0.1768

According to my Calculator for Two-Player Texas Hold 'Em, the chances of these two hands encountering each other are:

A7 wins = 53.52%
KJ wins = 46.10%
Tie = 0.39%

Although KJ suited is rated higher on my chart, it ranks lower than A7 unsuited in a direct matchup. Why is that?

Explaining this is quite complex. When two hands are set against one another, their interactions come into play. For instance, in the starting hand strength table, AK offsuit is just marginally above AQ offsuit, with expected values of .3064 and .2886, respectively. Nevertheless, when they compete, AK significantly outperforms AQ, illustrated by the following:

AK wins = 71.72%
AQ wins = 23.69%
Tie = 4.58%

In the clash between A7 offsuit and KJ suited, the ace overshadows both the king and the jack. The highest likelihood for the KJ player to win arises when they manage to pair one of their cards while avoiding any ace on the table. This scenario occurs only 37.73% of the time, with the additional 46.10% chance of winning derived from higher-ranking hands.

Even though A7 holds a strong position against KJ, it's typically more advantageous dominated than KJ by random hands.

This comparison may not be entirely apt, but it somewhat resembles the game rock paper scissors . Among experienced players, each move should approximately maintain equivalent power ratings. However, if one player picks paper while another chooses scissors, the individual power ratings don't hold weight, and scissors will emerge victorious.

A visitor on my Wizard of Vegas website asserts that specific modifications should be applied compared to the traditional multi-deck game. strategy where the dealer hits a soft 17:

• Hit soft 13 vs. 5 or 6
• Hit 2-card soft 15 vs. 4
• Hit 3,3 vs. 2

The rationale behind hitting soft hands is that you might draw a beneficial soft double afterward. Under this rule, the value of hitting threes increases because drawing an ace would contribute to a strong three-card double.

This topic was raised and explored within the forum of my partner site. Wizard of Vegas .

I'm not aware of a simple, non-recursive method for this calculation. However, a straightforward recursive solution does exist.

f(n)= pr(tails in first flip) × f(n-1) +
p(heads on the first flip, tails on the second flip) × f(n-2) +
p(heads on the first two flips, tails on the third flip) × f(n-3) +
p(heads on the first three flips, tails on the fourth flip) × f(n-4) +
p(heads on the first four flips, tails on the fifth flip) × f(n-5) +
p(heads on the first five flips, tails on the sixth flip) × f(n-6) +
p(heads on the first six flips, tails on the seventh flip) × f(n-7) +
pr(heads in first 7 flips) =

(1/2) × f(n-1) +
(1/2)²× f(n-2) +
(1/2)³× f(n-3) +
(1/2)⁴× f(n-4) +
(1/2)⁵× f(n-5) +
(1/2)⁶× f(n-6) +
(1/2)⁷× f(n-7) +
(1/2)⁷

Where:
f(n)=the likelihood of success within n flips.
pr(x) = probability of x happening.

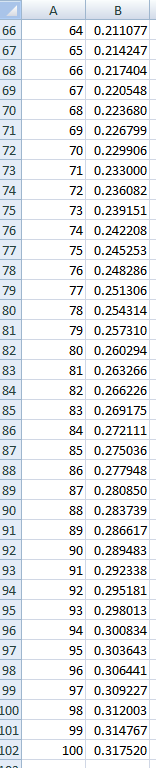
Spreadsheets are ideal for scenarios like this one. In the examples shown below, I've set the probabilities in cells B2 through B8 to 0, as it's impossible to get 7 heads in a row with 6 or fewer flips. For B9, I included the formula:

=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7

Next, I duplicated that formula from B10 to B102, which corresponds to a total of 100 flips, resulting in a probability of 0.317520. A simulated random test confirms this outcome.

On a side note, in case you are interested, the probability of witnessing at least one streak of 7 or more heads or tails stands at 54.23%. The likelihood of one or more occurrences of exactly seven heads is 17.29%.

---

Following the initial publication, Rick Percy shared his approach using matrix algebra with me. Here’s my interpretation. I assume the reader has a foundational understanding of matrix algebra.

Firstly, there are eight potential states that the flipper can occupy at any given time:

p₁= Probability of success when you require 7 more heads from this point.
p₂= Probability of success when you need 6 more heads from this point.
p₃= Probability of success when you need 5 more heads from this point.
p₄= Probability of success when you require 4 more heads from this point.
p₅= Probability of success when you need 3 more heads from this point.
p₆= Probability of success when you require 2 more heads from this point.
p₇= Probability of success when you only need 1 more head from this point.
p₈= Probability of success when no additional heads are needed = 1.

Let’s define the matrix S_nas the probability of being in each state after the nth flip,^thflip. S₀depicts the probabilities prior to the first flip, where there is a certainty of being in state 0. Thus, S₀=

  1 0 0 0 0 0 0 0  

Let T be the transformation matrix following two consecutive flips, or S'_nto S_n+1, where S_n+1= T × S_n

• In state 1, after one flip, there's a 0.5 likelihood of advancing to state 2 (if heads appears) and also a 0.5 likelihood of staying in state 1 (if tails appears).
• If in state 2, after one flip, you have a 50% chance of moving to state 3 (with heads), and a 50% chance of going back to state 1 (with tails).
• From state 3, after a flip, you stand a 50% chance of progressing to state 4 (if heads comes up) and a 50% chance of reverting to state 1 (if tails comes up).
• For state 4, a flip yields a 50% chance of advancing to state 5 (with heads), and a 50% likelihood of returning to state 1 (if tails occurs).
• Upon reaching state 5, a flip gives you a 50% probability of advancing to state 6 (if heads) and a 50% chance of going back to state 1 (if tails occur).
• In state 6, once again after a flip, you have a 50% chance of reaching state 7 (if showing heads) and a 50% chance of sliding back to state 1 (if tails happen).
• In state 7, continuing the pattern, your flip offers a 50% chance of moving to state 8 (with heads) and a 50% likelihood of returning to state 1 (if it's tails).
• Finally, in state 8, you've achieved your goal, and the probability of remaining in state 8 is 1.0.

Arranging all this into the transition matrix T =

0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0
0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0
0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0
0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0
0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0
0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0
0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0

To determine the probability of each state following a single flip...

(1) S₁= S₀× T

How about after two flips?

(2) S₂= S₁× T

Let’s replace equation (1) in equation (2)..

(3) S₂= S₀× T × T = S₀× T²

What about after 3 flips?

(4) S₃= S₂× T

Substituting equation (3) into (4)..

(5) S₃= S₀× T²× T = S₀× T³

We can continue this process up to the state after completing the 100th flip..

S₁₀₀= S₀× T¹⁰⁰

So, what is T¹⁰⁰? Before computers, solving such equations must have been incredibly tedious. Nevertheless, utilizing the MMULT function in Excel along with some copying and pasting allows us to find T'¹⁰⁰=

0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520
0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005
0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929
n
th
flip. S
=
1 0 0 0 0 0 0 0

The component in the upper right of the matrix reveals the probability of being in state 8 after making 100 flips, which amounts to 0.317520.

n+1 , where S , blackjack players typically engage in roughly 70 hands per hour. The chance of hitting a blackjack in a six-deck game is 24*96/combin(312,2)=4.75%. I will assume a tie for blackjack still allows for a stamp. Therefore, it ought to take roughly 30/0.0475=632 hands to complete the card, or approximately 9.02 hours.

The likelihood of filling the card within four hours, given that you play 280 hands, is 1 in 30,000 when playing one hand at a time. I suspect any player who accomplishes this feat in four hours must have been playing at least two hands simultaneously.

This topic was raised and explored within the forum of my partner site. n+1 .