Ask The Wizard #230
In today's news, a woman from Atlantic City achieved an incredible feat of rolling 154 times in a row before finally rolling a seven at the end. This record means she rolled two dice 154 times without hitting a seven. Calculating the odds, I found that this scenario has odds exceeding 1.5 trillion to 1. To put this into perspective, one is nearly 9,000 times more likely to win the Mega Millions lottery than to pull off 154 rolls in which none were sevens. Considering how exceedingly improbable this is, and noting that individuals are found guilty based on DNA evidence that has just billions to one odds of being a false positive, how suspicious would you be of potential cheating? Would you think it prudent to reach out to the Borgata casino for their insights? I've already contacted them, shared my details, and told them they could handle it as they see fit. I'm curious to hear your opinion on this matter. Borgata Initially, she rolled the dice a total of 154 times, with her final roll resulting in a seven out. However, this doesn't necessarily indicate that she didn't roll a seven throughout her first 153 attempts. It's entirely possible she rolled multiple sevens during the initial rolls. According to my calculations, the statistical likelihood of reaching the 154th roll is an astounding 1 in 5.6 billion. On the other hand, the odds of winning the Mega Millions lottery stand at 1 in 175,711,536. This highlights that rolling the dice 154 times without a seven is roughly 32 times more challenging. With sufficient time and sufficient gaming tables, I believe events like this were bound to occur eventually. Therefore, I don't suspect any foul play. My rough estimation suggests that the probability of this happening in any given year is around 1%.154You might also want to check out my solution presented through matrices at
According to Station Casinos, players receive free 'Mini X' bingo cards based on their spending levels, which is structured as follows: Source: NJ.com Each bingo card has five unique numbers, one corresponding to each letter in the word BINGO. The prizes awarded are as follows: May 3, 2003 column If no player covers in seven or fewer calls, a consolation prize of $50 is given to the first player who covers. combin I am curious about the expected value associated with each bingo card, specifically.
The table below illustrates that the value of the basic prizes is equivalent to 1/5 of one cent for each card. mathproblems.info , problem 204.
The value of the consolation prize allocated for each card is determined as 50/n, where 'n' represents the total number of cards in play. For instance, if there are 1000 cards in the game, the consolation prize value per card would amount to 5 cents.
Spend $1-$19 = 1 free card
Spend $20-$29 = 2 free cards
Spend $30-$39 = 3 free cards
Spend $40-$49 = 4 free cards
Spend $50-$59 = 5 free cards
Spend $60+ = 6 free cards
Strategy guide for double double bonus poker
Cover card in 5 numbers = $10,000
Cover card in 6 numbers = $3,000
Cover card in 7 numbers = $500
In double double bonus poker, a straight flush has a payout of 50, while a flush provides 6, and a straight offers 4. The chances of obtaining a straight flush are 2/47, for a flush are 7/47, and for a straight are 5/47. Therefore, the projected return could be calculated if you were to discard the 9.

I've heard that the game was removed from U.S. casinos due to patent infringement issues. According to the Fourth Quarter 2008 Statistical Report released by the Nevada Gaming Control Board, they documented the various table games present in Clark County.
Expected Value of Mini X Card
| Calls | Pays | Probability | Return |
| 5 | 10000 | 0.00000006 | 0.00057939 |
| 6 | 3000 | 0.00000029 | 0.00086909 |
| 7 | 500 | 0.00000087 | 0.00043455 |
| Total | 0.00000122 | 0.00188303 |
Sadly, they didn’t specify what the 243 'other' games are, which doesn't provide much clarity regarding your inquiry, but it's still a relevant point to mention.
On your video poker Dear sir, I recorded the outcomes of an automated single-zero roulette game across 8672 plays. My chosen number appeared an astonishing 278 times. I selected this number based on noticeable wear patterns in the pocket. How confident can I be that this number has a higher probability of occurrence than 1 in 37? , you state that if your are dealt 5 6
6 7
7 8
8 9
9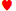 , that it is correct to hold the straight. It just seems counter-intuitive to me, but if you could explain in a little more detail about why going for the straight flush is poor strategy, I would be grateful.
, that it is correct to hold the straight. It just seems counter-intuitive to me, but if you could explain in a little more detail about why going for the straight flush is poor strategy, I would be grateful.
If I understand correctly, 'clocking the wheel' refers to predicting where the ball is likely to land by analyzing the speeds of the ball, its location, and the wheel's rotation. It appears that you might be capitalizing on a biased wheel, which represents a different form of advantage play. Additionally, another common strategy involves leveraging a 'dealer signature,' wherein the croupier's consistency leads to nearly identical speeds for the ball and wheel during each spin. This allows players to forecast the final resting place of the ball using its location and historical outcomes. is (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468. The expected return of the straight at 4 is much more.
is (2/47)×50 + (7/47)×6 + (5/47)×4 = 3.4468. The expected return of the straight at 4 is much more.
In response to your inquiry, statistically, you would expect to hit your number approximately 8672/37, equating to 234.38 times. The variance of this should be calculated as 8672×(1/37)×(36/37), resulting in 228.04. Consequently, the standard deviation will be the square root of the variance, which is about 15.10. You experienced 278 hits, exceeding the expected 234.38 by about 43.62 more hits. This translates to (43.62-0.5)/15.10 = 2.8556 standard deviations. The subtraction of 0.5 serves as an adjustment for utilizing a continuous model to predict a discrete one. By applying a Gaussian approximation, the likelihood of hitting your number that frequently, or even more often, is roughly 0.21%. Hence, it seems probable that you've detected a biased wheel. However, there's still a 1 in 466 chance that it was simply a fortunate streak.
Accurate strategies and insights for engaging in casino games such as blackjack, craps, roulette, and many more.
Clark County Table Game Count
| Game | Tables |
|---|---|
| 21 | 2537 |
| Roulette | 405 |
| Craps | 334 |
| Other | 243 |
| Baccarat | 233 |
| Three Card Poker | 208 |
| Pai Gow Poker | 194 |
| Mini baccarat | 143 |
| Let It Ride | 98 |
| Pai Gow | 80 |
| Wheel of Fortune (Big Six) | 37 |
| Caribbean Stud Poker | 22 |
| Sic Bo | 1 |
| Chuck-a-Luck | 1 |
Please verify your email and click on the link we sent to finalize your registration process.
Explore the Top Online Casinos in Your Region
Calculator for Lottery Jackpot Ticket Sales
Engage in thrilling slot tournaments featuring huge prize pools


