Ask The Wizard #227

There isn't an exact moment when confidence is fully established; it's a gradual process. Initially, I would need to understand what exactly is being tested and what the shooter predicts will happen. Every test has two types of errors associated with it. A highly skilled shooter might fail due to a streak of bad luck, while an average shooter might succeed thanks to fortunate circumstances. Of the two scenarios, I would prefer to avoid a false positive result. I believe a reasonable testing framework should aim for a 5% chance of a false negative and a 1% chance of a false positive.

For instance, let’s say someone claims they can roll a seven on average every seven attempts with the dice. Typically, a random shooter would manage to roll a seven once every six tries. Through trial and error, I've determined that to appropriately test both claims, the dice would need to be rolled 3,600 times, and to qualify, there should be 547 or fewer sevens recorded, which translates to one seven per every 6.58 rolls.

A skilled shooter, who statistically should roll a seven one in every seven attempts, would be expected to yield around 514.3 sevens, with a standard deviation of about 21. When applying the Gaussian model, the likelihood of this skilled individual managing to roll 548 or more sevens (the false negative scenario) stands at 5.7%. Conversely, a random shooter is expected to roll around 600 sevens, with a standard deviation of 22.36, yielding a probability of 0.94% for passing the test (the false positive scenario). The illustration below presents the potential outcomes for both skilled and random shooters. Should the results lie to the left of the green line, I would consider the shooter to have successfully passed the test, prompting me to place my bet on them.

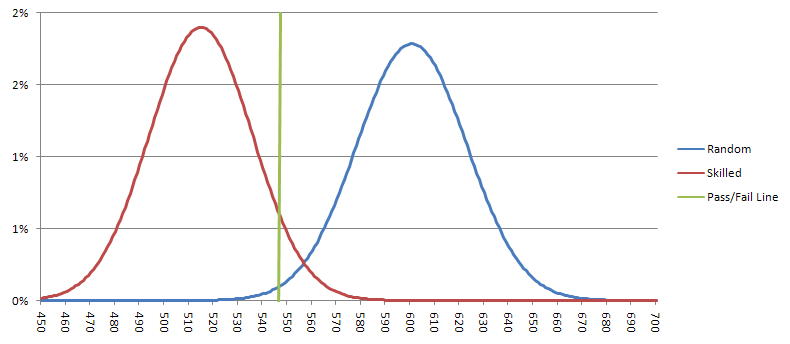
From a practical standpoint, if we assume the shooter can make two throws each minute, completing the test would take roughly 30 hours. I could perhaps consider being less strict about the significance level to reduce the time required, but that would compromise the strength of the results. It seems that a more extensive test beyond the 500-roll Wong experiment is now warranted.

I have not personally explored how card counting influences that specific bet, but Arnold Snyder has conducted research in that area, and his findings are available in his literature. According to him, one should place the bet in a six-deck game only during the final two decks, provided that the count reaches +10 or above using the Red Sevens method. In a double-deck scenario, he recommends betting in the last deck if the count is +6 or more. Big Book of Blackjack What advantages does a player gain when the house permits late surrender with a 6-deck shoe, especially when the house hits on a soft 17 versus when it stands on a soft 17? Does this yield different outcomes in an 8-deck shoe?

I've been considering how one could calculate the average number of rounds it would take to suffer a loss of ten units while consistently betting on the Player in baccarat. house-edge calculator Assuming an eight-deck game, the house edge for the Player bet is calculated at 1.2351%. Therefore, the expected number of hands needed to experience a loss of ten units comes out to 10 divided by 0.012351, which equals approximately 809.66 hands.

6 decks, dealer stands on soft 17: 0.0726%
8 decks, dealer stands on soft 17: 0.0758%
6 decks, dealer hits on soft 17: 0.0882%
8 decks, dealer hits on soft 17: 0.0916%

Ultimately, it comes down to the cards being the deciding factor. You would have rightfully won that round.

Please verify your email and click on the link we provided to finalize your registration process.