Ask The Wizard #171

You're indeed considering some binary elements correctly, but your strategy needs refinement. Firstly, aim to leave your opponent with an odd number of rows, each containing a single dot, if possible. If that's not achievable, decompose each row into its individual binary parts. For instance, the number 99 translates to 64 + 32 + 2 + 1. Next, total the frequency of each binary part across all rows. Your goal is then to execute a move that leaves your opponent with an even count of all binary components across the board.

Let’s examine a practical scenario. Imagine it’s your turn and the situation unfolds as follows.

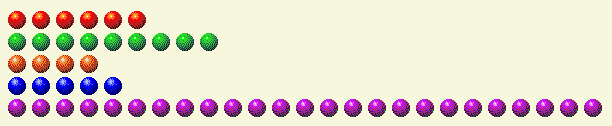
The following chart details how each row can be broken down into its binary elements.

Player’s Turn 1

Row	1	2	4	8	16
6	0	1	1	0	0
9	1	0	0	1	0
4	0	0	1	0	0
5	1	0	1	0	0
25	1	0	0	1	1
Total	3	1	3	2	1

You'll notice there's an odd count of ones, twos, fours, and sixteens. It's essential to reduce the row containing 25 to below 16 to eliminate the 16 value. To achieve an even total of binary elements, we should remove the 1, incorporate a 2, include a 4, maintain the 8, and discard the 16. Consequently, the best move is to remove 2, 4, and 8, totaling 14 in the last row, which results in the following configuration.

Computer’s Turn 1

Row	1	2	4	8	16
6	0	1	1	0	0
9	1	0	0	1	0
4	0	0	1	0	0
5	1	0	1	0	0
14	0	1	1	1	0
Total	2	2	4	2	0

Next, the computer takes its turn and presents this new configuration.

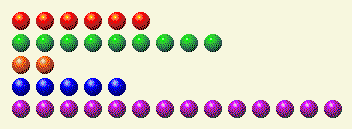
Here is the binary breakdown of that.

Player’s Turn 2

Row	1	2	4	8	16
6	0	1	1	0	0
9	1	0	0	1	0
2	0	1	0	0	0
5	1	0	1	0	0
14	0	1	1	1	0
Total	2	3	3	2	0

Now, we need to eliminate a 2 and a 4 to balance those totals. The only row available is 14, which has both components, so we'll remove 6, leaving us with 8.

Computer’s Turn 2

Row	1	2	4	8	16
6	0	1	1	0	0
9	1	0	0	1	0
2	0	1	0	0	0
5	1	0	1	0	0
8	0	0	0	1	0
Total	2	2	2	2	0

Next, the computer takes its turn and presents this new configuration.

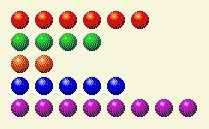
Now we need to change the 1, 4, and 8 columns.

Player’s Turn 3

Row	1	2	4	8	16
6	0	1	1	0	0
4	0	0	1	0	0
2	0	1	0	0	0
5	1	0	1	0	0
8	0	0	0	1	0
Total	1	2	3	1	0

We can achieve this by altering the 8 to create a 5, as outlined here.

Computer’s Turn 3

Row	1	2	4	8	16
6	0	1	1	0	0
4	0	0	1	0	0
2	0	1	0	0	0
5	1	0	1	0	0
5	1	0	1	0	0
Total	2	2	4	0	0

Next, the computer takes its turn and presents this new configuration.

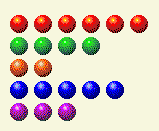
Now we need to change the 2 and 4 totals.

Player’s Turn 4

Row	1	2	4	8	16
6	0	1	1	0	0
4	0	0	1	0	0
2	0	1	0	0	0
5	1	0	1	0	0
3	1	1	0	0	0
Total	2	3	3	0	0

This can be done by changing the 6 to a 0.

Computer’s Turn 4

Row	1	2	4	8	16
0	0	0	0	0	0
4	0	0	1	0	0
2	0	1	0	0	0
5	1	0	1	0	0
3	1	1	0	0	0
Total	2	2	2	0	0

Next, the computer takes its turn and presents this new configuration.

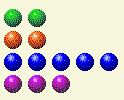
Now we need to change the 2s and 4s.

Player’s Turn 5

Row	1	2	4	8	16
0	0	0	0	0	0
2	0	1	0	0	0
2	0	1	0	0	0
5	1	0	1	0	0
3	1	1	0	0	0
Total	2	3	1	0	0

This adjustment can be performed by changing the 5 into a 3. If you manage to put your opponent in a position where they have identical pairs like x,x,y,y, you're setting yourself up for a guaranteed win, provided you maintain that pattern until the end.

Computer’s Turn 5

Row	1	2	4	8	16
0	0	0	0	0	0
2	0	1	0	0	0
2	0	1	0	0	0
3	1	1	0	0	0
3	1	1	0	0	0
Total	2	4	0	0	0

In the following moves, I ensure the computer remains within x,x,y,y configurations. Now the computer leaves me with 2,2,3,2; thus, I counter by leaving it with 2,2,2,2.

The computer then presents me with 2,2,1,2. I respond by leaving it with 2,2,1,1.

Next, the computer leaves me with 2,2,1. My move reduces it to 2,2. Achieving a scenario where your opponent has two equal rows almost guarantees your victory; just keep the rows the same.

The computer then places a single pile of 2 before me, and I choose to subtract 1.

Here is the end of the game.

I concur with your perspective. I generally advise against put or place bets for that reason; the odds favor making a line bet paired with maximum odds. Nevertheless, some players feel compelled to bet directly on points. If that’s the case, I would recommend selecting the most effective option among place, buy, and put bets, a topic I delve into with more detail in my craps section.

My blackjack appendix 9 This type of question is precisely what the system was designed for. Assuming a six-deck set, my analysis indicates that the expected value of doubling on an 8+2 versus a 7 stands at 0.396342, while the expected value for doubling on an 8+3 against a 10 is 0.176919. Thus, you are correct; the double down against a 7 is far more favorable.

Thanks for reaching out! The misunderstanding arises from considering the probability of drawing two of the 20 cards you need as a single event. The correct probability of drawing one of your 20 outs on the turn is 20/47 = 0.4255. If you miss the turn and then hit it on the river, the likelihood is (27/47)*(20/46) = 0.2498. Therefore, combining these probabilities yields a total probability of 0.4255 + 0.2498 = 0.6753.

I asked the Bone Man at nextshooter.com this one. Here is what he said.

When an incorrect player rolls the dice, it should be deemed a no-call and returned to the rightful shooter. While this is the standard procedure, the boxman may sometimes opt to allow the roll if the result benefits the majority of players. Additionally, players can request that the dice be passed to the next shooter to finish a hand, allowing for either the same or a fresh set of dice to be utilized. After completing the roll, the same shooter can play their hand again, allowing for multiple rounds.

I initiated an analysis using the normal approximation for this calculation, but the likelihood of exceeding 100 points is so minimal that it renders that method inaccurate. Instead, I conducted a random simulation comprising 8.25 million trials, in which 127 resulted in scores of 101 or above. Thus, the approximate probability stands at about 1 in 65,000.

When prizes escalate to life-altering sums, prudent players should adopt a more cautious approach, prioritizing risk aversion over maximizing expected value. A suitable strategy is to focus on maximizing expected satisfaction. I think a valuable metric for happiness could be the logarithm of total wealth. Consider an individual with wealth of $100,000 facing the choice between cases valued at $0.01 and $1,000,000. Opting for 'no deal' leads to an expected happiness of 0.5*log($100,000.01) + 0.5*log($1,100,000) = 5.520696. Let’s denote the bank offer as 'b', where the player feels indifferent to accepting it.

log(b) = 5.520696
b = 10^5.520696
b = $331,662.50.

This hypothetical player would feel indifferent at a bank offer of $331,662.50. Generally, the lower the initial wealth entering the game, the more conservative the approach should be. Typically, towards the game's latter stages, bank offers converge closely to expected value, sometimes slightly exceeding it. A rational scenario for winning a million would be if the player entered with substantial wealth or if the bank offers were exceptionally non-competitive. The producers seem to favor relatable, hardworking individuals, so it’s unlikely we’ll encounter someone reckless when substantial amounts are on the line. I’ve also never observed the bank making offers below 90% of expected value in the game’s final stretch. It's likely the person who wins a million will do so when an excessively daring gambler appears on the show, and in such a case, I’d be rooting for the banker.

I appreciate your question. To answer it effectively, it's important first to consider your motivation for gambling. If your primary goal is to minimize losses, the best choice is not to gamble at all. However, if your intent is to enjoy the thrill of gaming, I’d recommend opting for the $10 table with a 0.2% edge. While the expected loss remains constant, the larger bets will provide a more exciting experience.

Explore the Top Online Casinos Available in Your Region Pai Gow Poker side bets .

Engage in Slot Contests Offering Substantial Prize Pools

In this game, I always believed the secret to securing a win was to ensure the opponent, which here is a computer, is left with a quantity of dots that correlates to the next lowest number whose total matches the binary sum. For instance, if I have 17 dots and I take away 2, I leave 15, which is the binary sum of 1, 2, 4, and 8. However, this approach doesn't seem to produce the desired results. Am I on the right path or mistaken?

You're indeed thinking correctly regarding binary numbers, but that strategy isn't fully effective. First, aim to leave your opponent with an odd quantity of rows containing one dot each if you can. If that's not possible, break down each row into its binary components. For example, the number 99 can be represented as 64, 32, 2, and 1. Next, sum the quantity of each binary component from all the rows. Seek a move that will position your opponent to face an even number of all binary components across their rows.