Ask The Wizard #157
Imagine a betting game involving an unbiased coin flipped multiple times. Each flip costs us 1 rupee, and we're left with two outcomes: heads (H) or tails (T). If the difference between the counts of heads and tails reaches 3, we gain 8 rupees from the gambler. Should we participate in this game? How do we calculate our chances of winning? What happens to our likelihood of success if the payout changes to either 7 or 9 rupees?
Let’s denote x as the anticipated number of flips needed from the very beginning.
We will define y as the expected flips remaining when one side has a slight majority of one flip.
Let’s refer to z as the anticipated flips left when one side has a clear majority of two flips.
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
Using straightforward matrix calculations, we conclude that E(x) is 9, E(y) is 8, and E(z) is 5. Hence, on average, to achieve a gap of three between heads and tails, 9 flips will be necessary. Betting 8 rupees seems favorable for the bettor who is collecting 1 rupee per flip, as they can expect to make an average of 9 rupees with only an 8 rupee payout. This results in a house edge of 11.11% for the gambler. Conversely, at a 9-rupee bet, the odds are balanced, while at 7 rupees, the advantage shifts to 22.22% for the house.
Many people mistakenly think that sports betting limits in Las Vegas are exceedingly high, though in my experience, this is primarily true for football and not always the case. Can you provide details on the average betting limits in Vegas sportsbooks for the four major sports? I appreciate your assistance.
In my view, hockey does not qualify as a major sport since it garners very little interest. I've heard that casinos along the Coast tend to feature the highest betting limits. Although there aren’t any specific limits that are publicly known, they do accept significant bets based on individual circumstances. Here’s my estimate for typical betting limits on an average game.
NFL side: $50,000
NFL total: $5000
MLB money line: $10,000
MLB total: $2000
NBA side: $10,000
NBA total: $2,000
I've been with my boyfriend for a year, and he has a child from a previous relationship whom he seldom gets to see. He is seven years older than me, and I have concerns about his faithfulness. Early in our relationship, he engaged in flirtatious conversations with a former colleague while we were together. Lately, he has been going out every night and drinking excessively, and I discovered a text to a friend in which he mentioned still having feelings for this woman. He claims he only said this in a friendly context, but later that same evening, he texted another girl calling her attractive. I feel lost about what to do next. Do you think he is unfaithful?
There's a good chance he is cheating. Even if he hasn't physically cheated, the interactions you've mentioned certainly qualify as emotional cheating, which is still a betrayal. Based on the evidence you have, I would recommend considering ending the relationship.
In California, traditional Craps cannot be played. Instead, several casinos utilize card games simulating dice with A through 6 representing each side. I suspect that using multiple decks changes the odds (for example, with four decks, there would be 16 of each rank). Does this situation advantage the house like it does in blackjack, or does it provide an edge to the player? Players might adjust their bets based on the number of cards already played before a shuffle, assuming mid-shoe shuffles are involved.
You’re right; in Craps, dice alone don’t determine outcomes. There are multiple methods of substituting cards for dice while maintaining identical odds. One option is using two separate decks, eliminating any effect from card removal. Another method is to utilize a seven-card deck featuring the numbers 1 to 6, with a seventh card acting as a 'double.' If the double is drawn first, it is reshuffled; if drawn second, it takes the place of the first number. Regardless of how the casino employs the system, I have yet to encounter valid proof that the odds differ from those generated by using two regular dice. Thus, I believe there’s something missing in your explanation of the rules.
I enjoy visiting your website to read your game analyses and probability discussions. I have a query that I think someone familiar with the slot machine industry could answer. My girlfriend and I enjoy playing this particular three-reel slot machine that accepts quarter or dollar bets. The highlight of the game is when landing the 'hamburger lady' on the third reel, triggering a bonus round. In this bonus, players press a button to roll a virtual dice, which can land on numbers 1 through 6. As players traverse a hamburger theme, they gather credits and aim to reach the top for a bonus of 5,000 credits. My question is whether the bonus amount is determined before the round starts or if it is truly random since players must press the button after each roll. Certain rolls can terminate the bonus prematurely, but can players avoid these outcomes, or is the amount already set before the game even begins? I believe it’s predetermined, but my girlfriend disagrees. Could you clarify this for us?
Your girlfriend's stance is correct. The Nevada Gaming Control Board regulation 14.040.2(b) specifies that...
In simpler terms, any game representation involving dice must have the same probability as real dice. Therefore, it is impossible to fix the outcome ahead of time because any player could potentially roll any number throughout the game.
Dear Wizard, I've been reading your insights on online blackjack, noting that decks are shuffled after every hand. Is there an online casino option that offers less frequent shuffling, or must I play live dealer blackjack which generally involves a larger number of stacked decks, where I can at least anticipate when shuffling occurs? Thanks.
There may have been a misunderstanding regarding my earlier remarks. Ultimately, unless you are card counting, shuffling after every hand can actually be beneficial. The house edge diminishes from 0.02% in a six-deck game down to 0.11% in a single-deck game when shuffling occurs after each hand.
I wanted to inform you that while tickets can expire, in most cases, they can still be redeemed at the cage. Usually, the staff will cash them without raising any objections, and even if they do, they generally proceed with the transaction after some initial hesitation. blackjack appendix 10 You’re not alone in questioning my comments regarding the expiration dates for tickets. To address whether casinos accept expired tickets, I plan to conduct an experiment. On my next trip to the Strip, I will acquire tickets from various casinos and let them expire deliberately, then attempt to cash them in.
column where I explained the appropriate strategies for the game.
In my column dated November 28, 2002, I outlined the correct approach to take when only three rows remain. Here’s my tactic for four rows: during your turn, refer to the configuration on the left column and apply the corresponding action from the right column. For instance, the starting configuration of 3456 suggests you should remove 4 pearls from the row with 5, which results in 1346. If the left column indicates 'Lose,' winning is impossible if your opponent plays optimally, which seems to be the norm at Transcience. Feb 1, 2006 column A notable pattern in this setup is to position your opponent in a scenario where the combined count of pearls in the smallest row and the largest row equals that of the two middle rows. This includes ensuring zero pearls in the row holding the least quantity.
In your Nov 28, 2002 Brad S. contributed an overall strategy applicable regardless of the number of pearls and rows in play. First, analyze each row in terms of its binary components. For example, the initial setup for the Transcience game would appear as: Pearls Before Swine . They also have a sequel called Pearls Before Swine II . How do I beat this version?
Next, aim to maintain an even number of each power of 2. For the example above, there are two instances of 1's, two 2's, and three 4's. This results in one extra 4. Therefore, you should eliminate a 4 from any row that contains a 4. Continue this strategy until you reduce your opponent to a state of 2,2 or an odd count of 1's.
If you stick to this game plan, you'll find victory each time. Conversely, if your starting position is a losing setup, like I faced during game 10 (4+7+8+11), you can click 'go' so that your opponent makes the first move.
Pearls Before Swine II Strategy
| You Have | Leave |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | Lose |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | Lose |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | Lose |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | Lose |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | Lose |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | Lose |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | Lose |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | Lose |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | Lose |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | Lose |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | Lose |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | Lose |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | Lose |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | Loyalty Program |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
What are the odds that both pocket aces and pocket kings are dealt to players in the same hand?
- Play
- Read Review
- Home
- ›
The likelihood of one player receiving aces is calculated as follows: (4 choose 2) / (combin(52,2)) = 6/1326. The chance of the next player drawing a pair of kings stands at (combin(4,2) / combin(50,2)) = 6/1225. Considering there are 10 players, any one of whom could receive the aces, and 9 players for the kings, a rough estimate is 10*9*(6/1326)*(6/1225) = 0.001995, or about 1 in 501. This estimate might be slightly high, as it double-counts instances where two players end up with aces or two with kings, or both.
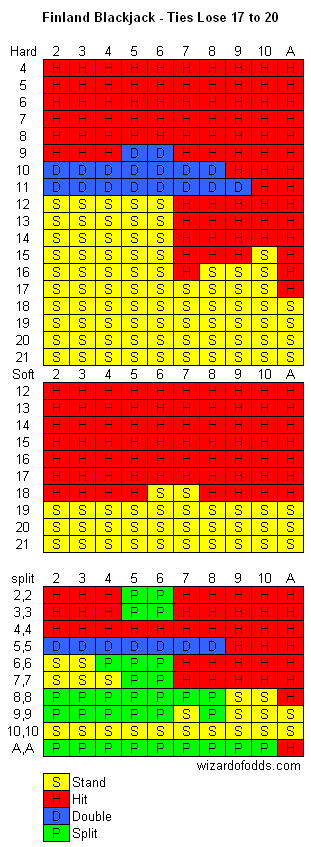
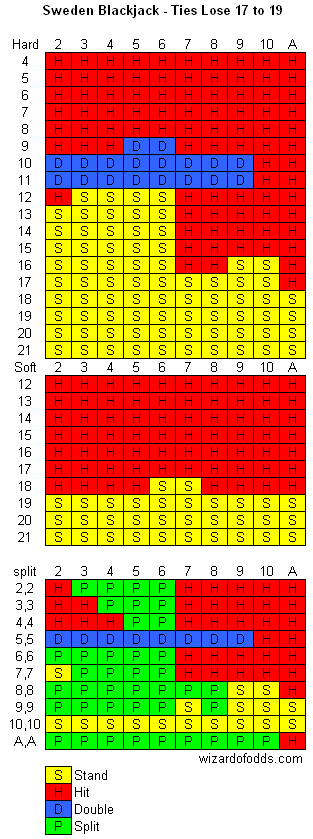
Ask The Wizard › Hello! Where can we find the best basic strategy for Club Blackjack as played in Finland, Sweden, and on Baltic Ferries? This game involves six decks, allows for natural hit busts, double down on 9-11, one split, no double after split, and the dealer takes ties on 17-20 (or 17-19 in Sweden). We acknowledge that this is a game with a substantial house edge of nearly 9%, but it's our only option for gaming, and since winning isn’t likely, we want to go down fighting like good soldiers should. Thank you!
I recall seeing those rules during my visit to Helsinki back in 1986. At that age of 20, I must admit I participated in the game, despite being underage in the U.S. It was a while before I became the Wizard. Remarkably, it was the first legal blackjack game I ever played, and ironically, a single-zero roulette table was right next to it.
Explore the finest online gambling establishments available in your region. Ask The Wizard #157 Tool for calculating the potential earnings from lottery jackpot tickets.
Participate in slot competitions offering substantial cash prizes.
Imagine you engage in a gambling activity involving a fair coin that’s flipped multiple times. Each flip costs 1 rupee. There are two outcomes: heads or tails. If the number of heads and tails differs by 3, you will earn 8 rupees from your opponent. Should you take this risk, and what would your reasoning be? Additionally, what is your likelihood of winning this game, and how does it change if the winning amount is 7 or 9 rupees?
Let’s designate x as the anticipated number of flips starting from the initial position.
 |  |
We’ll assign y to denote the expected number of flips left when one side of the coin has a single flip in the majority.
Let’s define z as the anticipated number of flips remaining when one side has two flips in the majority.
By applying straightforward matrix calculations, it’s clear that E(x) = 9, E(y) = 8, and E(z) = 5. This indicates that, on average, achieving a difference of 3 between heads and tails requires 9 flips. Since you're betting 1 rupee per flip to potentially gain 8 rupees, this bet appears favorable, as expected earnings of 9 rupees exceed your stake of 8 rupees. Consequently, the house edge stands at 11.11%. Should you win 9 rupees, it’s a balanced game; however, at 7 rupees, the house advantage jumps to 22.22%.
There's a common belief that betting limits for sports in Las Vegas are exceptionally high, but from my experience, this is mainly true for football and not universally applicable. Could you provide an estimate of the betting limits for the four primary sports at Las Vegas sportsbooks? I appreciate your assistance. E(z) = 1 + 0.5*E(y) I don’t consider hockey a major sport since it tends to receive minimal betting interest. I've heard that casinos on the coast have the most generous limits. While I’m unaware of any fixed maximum, they evaluate large bets individually. Here’s my estimation of what they might accept on average for a typical game.
My boyfriend and I have been in a relationship for a year. He has a child with his ex, but he rarely sees her. He is seven years older than me, and I have growing concerns about his fidelity. Early in our relationship, he had inappropriate conversations with a former coworker while spending time with me. Recently, he’s been going out every night, often returning drunk, and I discovered a message in which he confessed to having feelings for her. He claims it was merely in a friendly context, but later that night, he referred to another woman as sexy. I'm at a loss on what to do next; do you think he's being unfaithful?
It’s quite likely that he is. Even if he hasn't physically cheated, the behaviors you've observed can be considered lesser forms of infidelity. Based solely on the evidence you have, I would recommend moving on.
Traditional Craps are not permitted in California. Here, several casinos utilize cards that mimic dice, designating A, 2, 3, 4, 5, and 6 to represent the dice sides. I assume that using multiple decks changes the odds (for instance, 4 decks would include 16 of each number). Does this alter the probabilities in favor of the house, similar to blackjack, or does it provide an advantage to players? Players are capable of making higher or lower bets based on the cards already played before a shuffle (assuming they shuffle mid-play).
NFL side: $50,000 NFL total: $5000 You are correct; the outcome in craps isn’t determined solely by the dice. There are various methods of substituting cards for dice while maintaining the same odds. One method involves using two separate decks, which eliminates the removal effect. Another strategy could use a 7-card deck consisting of numbers 1 to 6, along with a seventh 'double' card. In this setup, the first drawn card cannot be the double; if it is, it goes back in, and drawing resumes. Drawing the double on the second turn counts as the first card’s value. Regardless of the casino's approach, I've never encountered convincing evidence of discrepancies in odds compared to traditional dice. Thus, it seems crucial to adhere to the established rules.
I enjoy visiting your website and reading your analyses of various games and their probabilities. I'm curious about a particular slot machine my girlfriend and I enjoy playing. It’s a classic three-reel slot, with either quarter or dollar bet options. The exciting part occurs when the 'hamburger lady' appears on the third reel, triggering a bonus game. This game involves pressing a button to make a virtual die roll between 1 and 6, moving along the hamburger to accumulate credits and aiming to reach the top for a grand prize of 5,000 credits. My question is whether the bonus payout is predetermined before the game starts or if it’s entirely random since the player must push a button after every die movement. There are elements of the bonus game where specific rolls can end the game early; can players prevent these premature endings, or is the bonus amount fixed from the outset? I believe the bonus is predetermined, but my girlfriend disagrees. Can you clarify this dispute?


